Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Tripeptide_loop_closure

Authors: F. Cazals and T.O'Donnell

Introduction

This package provides tools to generate or modify tripeptide segments in protein structure, using the so-called Tripeptide Loop Closure (TLC). These tools encompass low level C++ code, as well as the application $\text{\sbltlc}$. The reader is referred to [148] for a detailed description.

Classical TLC.. Mathematically, consider a tripeptide whose internal coordinates (bond lengths ${d_i}$, valence angles ${\theta_i}$, and dihedral angles $({\phi_i, \psi_i, \omega_i}$) have been extracted / are known. The TLC problem consists of finding all geometries of the tripeptide backbone compatible with the internal coordinate values $ ( d_i, \theta_i ) $ (Fig. fig-TLC-example).

Solving the problem requires finding the real roots of a degree 16 polynomial, which also means that up to 16 solutions may be found [157], [64].

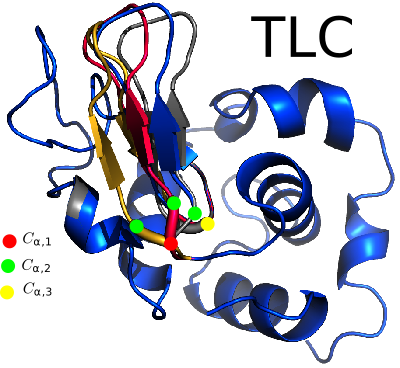
TLC: example reconstructions.

TLC with gaps. A generalization of the classical TLC consists of considering three amino acid which are not not contiguous along the backbone (Fig. fig-TLCG-example).

This case is of interest in the presence of three linkers enclosing two rigid SSE. Mathematically, this is akin to the original problem, with the rigid blocks modeled as fictitious bonds separating the amino acid (Fig. fig-TLCG-example for one example).

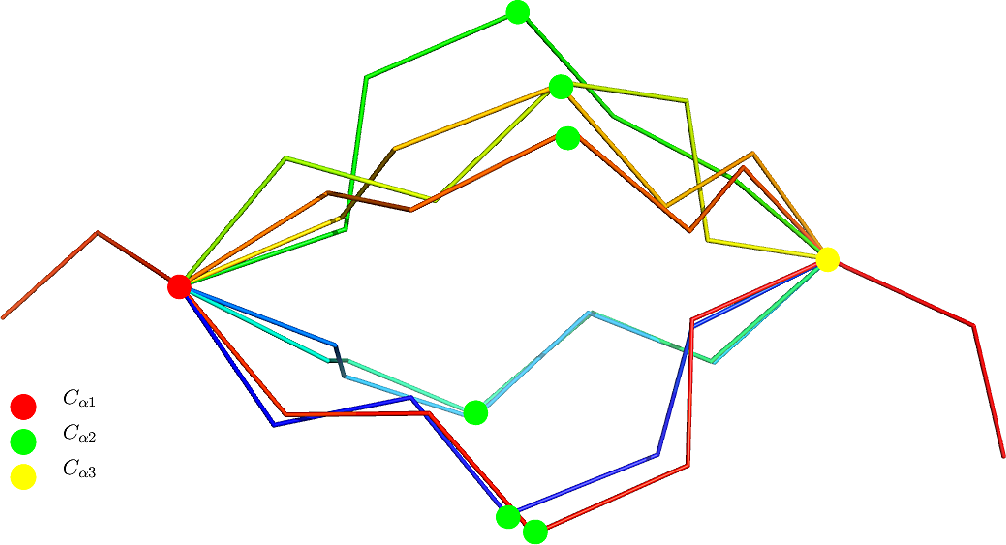
TLCG: example reconstructions sandwiching a beta sheet. PDBID 1vfb, chain C. The three amino acid defining the tripeptide are: $\Calpha{1}$ (resid: 41 GLN), green $\Calpha{2}$ (resid: 42 ALA), yellow $\Calpha{3}$ (resid: 54 GLY). A total of four reconstructions were obtained; the blue one represents the original geometry.

Algorithms

Our implementation follows [64], except for numerics and the handling on internal coordinates other than the dihedral angles.

TLC and internal coordinates. Solving a particular TLC problem puts the focus on dihedral angles, so that that there are three options to handle the other internal coordinates (bond length and valence angles):

  • data internals: using those found in the tripeptide processed,
  • canonical internals: using standard values for fixed internals, as done in the original version [64] ,
  • user-defined-internals: using values defined by the user and passed in a file – see example below.
#6 bond lengths from CA1C1 to N3CA3
1.33 1.52 1.45 1.33 1.52 1.45
#7 bond angles from N1CA1C1 to N3CA3C3
1.95 2.05 2.01 1.95 2.05 2.01 1.95
#Omega torsion angles
3.14 3.14

Algorithm. First, the constraints and position of anchors around the loop closure are extracted. These atoms are $N_1, \Calpha{1}, \Calpha{2}, \Calpha{3}$ (Fig. fig-TLC ). The algorithm proceeds with the following three steps:

  • Step 1: Formulate the 16th degree polynomial using constraints and anchor coordinates ([64]). Nb: the number of solutions lies in the range 0 to 16.
  • Step 2: Compute the polynomial roots of the polynomial.
  • Step 3: Compute the coordinates i.e. the embedding corresponding to each root.

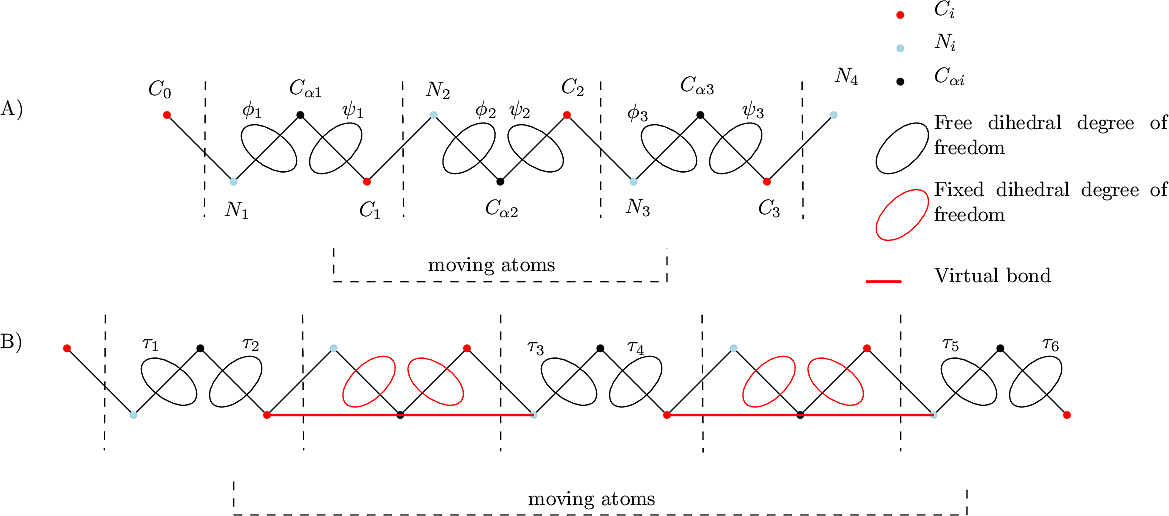Tripeptide: atoms and degrees of freedom used for loop closure. (A) Classical tripeptide loop closure(TLC), the six dihedral angles represented correspond to the degrees of freedom used to solve the problem. (B) In tripeptide loop closure with gaps(TLCG), the dihedral degrees of freedom $\tau_i$ may not be contiguous – they are separated by red gaps on the Figure.

(NEW) Design and classes

Main classes


TLC constraints. Consist of the positions of anchors (2 legs i.e. four points), and the remaining internal coordinates (6+7+2).


TLC constraints and associated loader.
The constraints used to solve TLC are (i) the positions of the anchors (left and right legs), and (ii) the remaining internal coordinates, namely bond lengths (6 values), valence angles (7 values), and torsion angles (2 values, omega angles).

The main classes defining and loading these constraints are


TLC options. The options used by TLC encompass

  • The resids defining TLC,
  • The type of constraints used,
  • Selected visualization options.

These options are managed in the following class, which also provides the associated command line parsing:

template <class ProteinRepresentation> class SBL::CSB::T_TLC_options (TLC_options.hpp)


Main algorithm. The main algorithm takes as input a protein representation and the TLC options. It consists of the following steps:

  • Load/specify the TLC constraints,
  • Solve TLC,
  • Generate the embeddings of all solutions.

The corresponding class, which is parameterized by a Traits class defined the required types, is:

template <class Traits> class T_Tripeptide_loop_closure_engine


Application. The final application undertakes the following steps

  • Parses the command line
  • Load the PDB file and select the chain,
  • Runs the main algorithm.

Advanced


Algebra.

  • template<class Algebraic_Kernel=CGAL::Algebraic_kernel_d_1<CGAL::Gmpq>> class T_Tripeptide_loop_closure;
  • template<class Algebraic_Kernel=CGAL::Algebraic_kernel_d_1<CGAL::Gmpq>> class T_Tripeptide_constraints_to_polynomial;
  • template<class Algebraic_Kernel=CGAL::Algebraic_kernel_d_1<CGAL::Gmpq>> class T_Polynomial_solver_interface;
  • template<class Algebraic_Kernel=CGAL::Algebraic_kernel_d_1<CGAL::Gmpq>> class T_TLC_polynomial_roots_to_embedings;

Algebra. Four classes following the steps of the algorithm are provided:

These three classes have an algebraic kernel as single template argument(default CGAL::Algebraic_kernel _d_1<CGAL::Gmpq>>). This kernel defines the polynomial type in step 1, the solver in step 2 and the Roots Number type in step 3. These three classes are implemented in a fourth interface class SBL::CSB::T_Tripeptide_loop_closure were all the steps are performed using the same kernel.

Robustness. The numerical stability of an algorithm is key to its robustness [33]. The aforementioned three steps use two number types:

  • $\text{\codecx{CGAL::Gmpfr}}$, a representation based on the $\text{\mpfr}$ library [95] supplying a fixed precision floating point number type.
  • ANT: Algebraic Number Type, obtained from the algebraic kernel AK, with default AK::Algebraic_real_1.

Using these, the three steps go as follows:

  • Step 1: $\text{\codecx{CGAL::Gmpfr}}$ is used to carry out all calculations including those with Pi. The number obtained are converted to ANT to obtain the polynomial.
  • Step 2: root finding is done using ANT
  • Step 3: roots are converted into $\text{\codecx{CGAL::Gmpfr}}$; embedings ie atomic coordinates are obtained using the $\text{\codecx{CGAL::Gmpfr}}$ type. Finally, when PDB files are dumped, $\text{\codecx{CGAL::Gmpfr}}$ are converted to doubles.

Utilities. A separate class (SBL::CSB::Tripeptide_loop_closure_utilities) with a number of useful low level static methods, in particular matrix operation functions using arrays.

A number of operations on internal coordinates from the package Molecular_coordinates are used:

  • Bond angle computation using two vectors.
  • Dihedral angle computation using three vectors.
  • Computing the embedding of a point in a reference frame defined by three others. Internal coordinates must be given: a bond length, a bond angle and a proper dihedral angle.

Application

This package provides the executable $\text{\sbltlc}$.

Command line options

  • The main input (see thereafter) is a PDB file together with a chain id and the resids of the three amino acids providing the six dihedral angles used to solve TLC.
  • The output consists of one PDB file for each solution. By default, each solution file solely contains the backbone heavy atoms of the region of affected by TLC. That is, if the three amino acids are consecutive, each solution file contains 9 atoms. Note that side chain atoms are not placed since optimizing coherently side chains is a problem in itself. Note also that the occupancy and temperature factors are omitted, since they make no sens in this context.

More specifically, the main options of $\text{\sbltlc}$ are as follows:

The main options of the program $sbl-tripeptide-loop-closure.exe$ are:
–filename string: Input pdb file(must have .pdb suffix
–chainid string: id of the chain in which the loop is found
–resids string: resids(idn) concateneted with eventual insertion codes(cn) in the format id1c1-id2c2-id3c3
–precision-factor float: Multiplicative factor (double $>1$) for the number of bits in the mantissa
–data-internals bool: Use the internals found in data. (Nb: all backbone atoms in the loop must be present in the file)
–standard-internals bool: Use standard internal values
–user-defined-internals string: specify internal value constraints from a file
–user-defined-internals bool: specify internal value constraints from a file
–directory-output string: Folder where output files will be stored
–output-prefix string: prefix for output files
–help bool: print the above option details


The following comments are in order:

  • The filename chain id and residue id are mandatory.
  • If the residue are not consecutive then a tripeptide loop closure with gaps is implemented (TLCG, Fig. fig-TLCG-example ). The residues in between are then replaced into position in a rigid motion in between the residues specifying the tripeptide.
  • Numerics in $\text{\sbltlc}$. The executable $\text{\sbltlc}$ makes it possible to specify the precision used for calculations, based on the number type $\text{\codecx{CGAL::Gmpfr}}$. Practically, denoting x this multiplicative factor: $x=1$: $\text{\sbltlc}$ uses the plain double precision; $x=2$: $\text{\sbltlc}$ uses a double double precision; $x=4$: $\text{\sbltlc}$ uses a quadrice double precision; etc.
TLC with gaps deserves the following comment:
  1. Standard internals cannot be used in this setting, naturally.
  2. User-defined internals do apply, but the user must provide distances and angles coherent with the geometry of the virtual bodies corresponding to the gaps. See [148] .


File formats

The format for user provided internal coordinates is as follows:

  • First line: 6 bond length
  • Second line: 7 bond angles(radii)
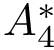
  • Third line: 2 $\omega$ torsion angles(radii)
#6 bond lengths from CA1C1 to N3CA3
1.33 1.52 1.45 1.33 1.52 1.45
#7 bond angles from N1CA1C1 to N3CA3C3
1.95 2.05 2.01 1.95 2.05 2.01 1.95
#Omega torsion angles
3.14 3.14

We note in passing that the following default values are used: 

#Bond lengths ac cn na ac cn na
1.52 1.33 1.45 1.52 1.33 1.45
#Bond angles nac acn cna nac acn cna nac
1.947 2.050 2.093 1.947 2.050 2.093 1.947
#Omega torsion angles
3.14159265359 3.14159265359

Viewing the results with VMD

Assume that a number of solutions have been generated. For example, consider the 8 solutions of the following call, corresponding to changes in a loop of an antibody: 

(old) sbl-tripeptide-loop-closure.exe --filename 1vfb.pdb --chainid A --resids 11-13-15 -o solutions
(new) sbl-tripeptide-loop-closure.exe -f 1vfb.pdb --load-chains A --resids 11-13-15 --odir solutions

We provide the script $SBL_DIR/scripts/vmd/load-pdbs.vmd, which can be used as follows 

vmd -e /path/to/vmd/script/load-pdbs.vmd -args original/pdb/file.pdb solutions*.pdb

Viewing the results with Pymol

In the context of the previous section, all input PDB files can be passed at once to pymol: 

pymol input-file.pdb solutions*.pdb

Visualization, Plugins, GUIs

The SBL provides VMD, PyMOL, and Web plugins for sbl-tripeptide-loop-closure.exe. Launch the VMD plugin from the SBL catalog under the Extensions menu, start the PyMOL plugin by running sbl_tripeptide_loop_closure in the PyMOL command line, and open the Web plugin from the SBL web plugins launcher page (served locally via sbl-web-plugins-launcher). All three plugins expose the same GUI and capabilities.

sbl-tripeptide-loop-closure plugin user interface.
The user interface for the sbl-tripeptide-loop-closure plugin. The typical workflow is: Step 1: Provide input file. Step 2: Specify the chain id and the three residue ids. Step 3: Choose an output directory (optional, a default is provided). Step 4: Launch the computation. Step 5: Inspect the conformation solutions in the viewer. Step 6: (Optional) Use the update panel to select separate solution to view.

Jupyter demo

See the following jupyter notebook:

  • Jupyter notebook file
  • Tripeptide_loop_closure

    Tripeptide_loop_closure

    Compute and visualize solutions in python

    In [ ]:
    import os
import nglview as nv

    The options of sbl-Tripeptide-loop-closure are:

    --filename, Input pdb file(must have .pdb suffix}
--chainid, id of the chain in which the loop is found
--resids, resids(idn) concateneted with eventual insertion codes(cn) in the format id1c1-id2c2-id3c3
--precision-factor, Multiplicative factor (double \eql{>1}) for the number of bits in the mantissa
--data-internals, Use the internals found in data. (Nb: all backbone atoms in the loop must be present in the file)
--standard-internals,  Use standard internal values
--user-defined-internals, specify internal value constraints from  a file
--directory-output,  Folder where output files will be stored
--output-prefix, prefix for output files
--help, print the above option details
    In [ ]:
    #create output folder
outputfolder="results"
if not os.path.exists(outputfolder):
    os.mkdir(outputfolder)
    
#Generate Tripeptide loop closure solutions
os.system("sbl-tripeptide-loop-closure.exe --filename data/1vfb.pdb --chainid A --resids 11-13-15 --output-prefix data_ --directory-output results")
os.system("sbl-tripeptide-loop-closure.exe --filename data/1vfb.pdb --standard-internals --chainid A --resids 14-15-16 --output-prefix std_  --directory-output results")
os.system("sbl-tripeptide-loop-closure.exe --filename data/1vfb.pdb --user-defined-internals constraints.txt --chainid A --resids 14-15-16 --output-prefix specified_constraints_  --directory-output results")

    Visualize original file:

    In [ ]:
    view = nv.show_file("data/1vfb.pdb")
view

    Visualize data extracted internals second solution:

    In [ ]:
    view = nv.show_file("results/data_1vfb-solution-2.pdb")
view

    Visualize standard internals second solution:

    In [ ]:
    view = nv.show_file("results/std_1vfb-solution-2.pdb")
view

    Visualize user defined internals second solution:

    In [ ]:
    view = nv.show_file("results/specified_constraints_1vfb-solution-2.pdb")
view
    In [ ]: