D. Agarwal, J. Araujo, C. Caillouet, F. Cazals, D. Coudert, and S. Pérennes. Connectivity inference in mass spectrometry based structure determination. In H.L. Bodlaender and G.F. Italiano, editors, European Symposium on Algorithms (Springer LNCS 8125), pages 289–300, Sophia Antipolis, France, 2013. Springer.

D. Agarwal, C. Caillouet, D. Coudert, and F. Cazals. Unveiling contacts within macro-molecular assemblies by solving minimum weight connectivity inference problems. Molecular and Cellular Proteomics, 14:2274–2282, 2015.

N. Akkiraju and H. Edelsbrunner. Triangulating the surface of a molecule. Discrete Appl. Math., 71:5–22, 1996.

N. Akkiraju and H. Edelsbrunner. Triangulating the surface of a molecule. Discrete Applied Mathematics, 71(1):5–22, 1996.

F. Alber, F. Förster, D. Korkin, M. Topf, and A. Sali. Integrating diverse data for structure determination of macromolecular assemblies. Ann. Rev. Biochem., 77:11.1–11.35, 2008.

Eric Alcaide, Stella Biderman, Amalio Telenti, and M Cyrus Maher. Mp-nerf: A massively parallel method for accelerating protein structure reconstruction from internal coordinates. Journal of Computational Chemistry, 43(1):74–78, 2022.

Mohammed AlQuraishi. Parallelized natural extension reference frame: parallelized conversion from internal to cartesian coordinates. Journal of computational chemistry, 40(7):885–892, 2019.

Simon L Altmann. Rotations, quaternions, and double groups. Courier Corporation, 2005.

N. Amenta, S. Choi, and R. Kolluri. The power crust, unions of balls, and the medial axis transform. Computational Geometry : Theory and Applications, 19(2):127–153, 2001.

R. Andonov, N. Yanev, and N. Malod-Dognin. An efficient lagrangian relaxation for the contact map overlap problem. WABI, pages 162–173, 2008.

R. Andonov, N. Malod-Dognin, and N. Yanev. Maximum Contact Map Overlap Revisited. J. of Computational Biology, 18(1):1–15, January 2011.

D. Arthur and S. Vassilvitskii. k-means++: The advantages of careful seeding. In ACM-SODA, page 1035. Society for Industrial and Applied Mathematics, 2007.

Ali Rana Atilgan, SR Durell, Robert L Jernigan, Melik C Demirel, O Keskin, and Ivet Bahar. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophysical journal, 80(1):505–515, 2001.

W. Atisattapong and P. Maruphanton. Obviating the bin width effect of the 1/t algorithm for multidimensional numerical integration. Applied Numerical Mathematics, 104:133–140, 2016.

J. Baker, A. Kessi, and B. Delley. The generation and use of delocalized internal coordinates in geometry optimization. The Journal of chemical physics, 105(1):192–212, 1996.

A. Banyaga and D. Hurtubise. Lectures on Morse Homology. Kluwer, 2004.

David J Barlow and JM Thornton. Ion-pairs in proteins. Journal of molecular biology, 168(4):867–885, 1983.

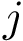
Mahsa Bayati, Miriam Leeser, and Jaydeep P Bardhan. High-performance transformation of protein structure representation from internal to cartesian coordinates. Journal of Computational Chemistry, 41(24):2104–2114, 2020.

R. Belardinelli, S. Manzi, and V. Pereyra. Analysis of the convergence of the 1/ t and Wang-Landau algorithms in the calculation of multidimensional integrals. Physical Review E, 78(6):067701, 2008.

M. Betancourt. A conceptual introduction to Hamiltonian Monte Carlo. arXiv preprint arXiv:1701.02434, 2017.

G. Biau and L. Devroye. Lectures on the nearest neighbor method. Springer, 2015.

G. Biau, F. Chazal, D. Cohen-Steiner, L. Devroye, and C. Rodriguez. A weighted k-nearest neighbors density estimate for geometric inference. Electronic Journal of Statistics, 5(204-237), 2011.

P. Bille. A survey on tree edit distance and related problems. Theoretical computer science, 337(1-3):217–239, 2005.

R. Blankenbecler, M. Ohlsson, C. Peterson, and M. Ringnér. Matching protein structures with fuzzy alignments. PNAS, 100(21):11936–11940, 2003.

A. Blum, J. Hopcroft, and R. Kannan. Foundations of data science. Cambridge, 2020.

J.-D. Boissonnat and M. Yvinec. Algorithmic geometry. Cambridge University Press, UK, 1998. Translated by H. Brönnimann.

J-D. Boissonnat, C. Wormser, and M. Yvinec. Curved voronoi diagrams. In J.-D. Boissonnat and M. Teillaud, editors, Effective Computational Geometry for curves and surfaces. Springer-Verlag, Mathematics and Visualization, 2006.

R. Bott. Morse theory indomitable. Publications Mathématiques de l'IHÉS, 68(1):99–114, 1988.

B. Bouvier, R. Grunberg, M. Nilgès, and F. Cazals. Shelling the Voronoi interface of protein-protein complexes reveals patterns of residue conservation, dynamics and composition. Proteins: structure, function, and bioinformatics, 76(3):677–692,

P. Braun, M. Tasan, M. Dreze, M. Barrios-Rodiles, I. Lemmens, H. Yu, J. Sahalie, R. Murray, L. Roncari, A-S. De Smet, K. Venketesan, J-F. Rual, J. Vandenhaute, M.E. Cusick, T. Pawson, D.E. Hill, J. Tavernier, J.L. Wrana, F.P. Roth, and M. Vidal. An experimentally derived confidence score for binary protein-protein interactions. Nature methods, 6(1):91–97, 2008.

Scott Brown, Nicolas J. Fawzi, and Teresa Head-Gordon. Coarse-grained sequences for protein folding and design. Proc Natl Acad Sci U S A, 100(19):10712–10717, Sep 2003.

Peter Bürgisser and Felipe Cucker. Condition: The geometry of numerical algorithms, volume 349. Springer Science & Business Media, 2013.

P. M. M. De Castro, F. Cazals, S. Loriot, and M. Teillaud. Design of the cgal spherical kernel and application to arrangements of circles on a sphere. Computational Geometry: Theory and Applications, 42(6-7):536–550,

F. Cazals and D. Cohen-Steiner. Reconstructing 3D compact sets. Computational Geometry Theory and Applications, 45(1-2):1–13, 2011.

F. Cazals and T. Dreyfus. Multi-scale geometric modeling of ambiguous shapes with toleranced balls and compoundly weighted 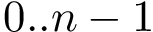α-shapes. In B. Levy and O. Sorkine, editors, Symposium on Geometry Processing, pages 1713–1722, Lyon, 2010.

F. Cazals and T. Dreyfus. The Structural Bioinformatics Library: modeling in biomolecular science and beyond. Bioinformatics, 7(33):1–8, 2017.

F. Cazals and A. Lhéritier. Beyond two-sample-tests: Localizing data discrepancies in high-dimensional spaces. In P. Gallinari, J. Kwok, G. Pasi, and O. Zaiane, editors, IEEE/ACM International Conference on Data Science and Advanced Analytics, Paris, 2015.

F. Cazals and N. Malod-Dognin. Shape matching by localized calculations of quasi-isometric subsets,with applications to the comparison of protein binding patches. In L. Wessels and M. Loog, editors, International Conference on Pattern Recognition in Bioinformatics, Delft, the Netherlands, 2011. Lecture Notes in Computer Science 7036.

F. Cazals and D. Mazauric. Optimal transportation problems with connectivity constraints. Research Report 8991, Inria Sophia Antipolis ; Université Côte d'Azur, 2016.

F. Cazals and R. Tetley. Characterizing molecular flexibility by combining lRMSD measures. Proteins: structure, function, and bioinformatics, 87(5):380–389,

F. Cazals and R. Tetley. Multiscale analysis of structurally conserved motifs. Preprint, NA(NA), 2020.

F. Cazals, F. Proust, R. Bahadur, and J. Janin. Revisiting the Voronoi description of protein-protein interfaces. Protein Science, 15(9):2082–2092, 2006.

F. Cazals, H. Kanhere, and S. Loriot. Computing the volume of union of balls: a certified algorithm. ACM Transactions on Mathematical Software, 38(1):1–20, 2011.

F. Cazals, T. Dreyfus, S. Sachdeva, and N. Shah. Greedy geometric algorithms for collections of balls, with applications to geometric approximation and molecular coarse-graining. Computer Graphics Forum, 33(6):1–17, 2014.

F. Cazals, T. Dreyfus, D. Mazauric, A. Roth, and C.H. Robert. Conformational ensembles and sampled energy landscapes: Analysis and comparison. J. Comp. Chem., 36(16):1213–1231, 2015.

F. Cazals, D. Mazauric, R. Tetley, and R. Watrigant. Comparing two clusterings using matchings between clusters of clusters. ACM J. of Experimental Algorithms, 24(1):1–42, 2019.

F. Cazals, B. Delmas, and T. O'Donnell. Fréchet mean and 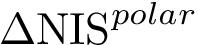p-mean on the unit circle: decidability, algorithm, and applications to clustering on the flat torus. In D. Coudert and E. Natale, editors, Symposium on Experimental Algorithms, Sophia Antipolis, 2021. Lipics.

F. Cazals, J. Herrmann, and E. Sarti. Simpler protein domain identification using spectral clustering. NA(NA), 2024. https://www.biorxiv.org/content/10.1101/2024.02.10.579762v1.

F. Cazals. Revisiting the Voronoi description of Protein-Protein interfaces: Algorithms. In T. Dijkstra, E. Tsivtsivadze, E. Marchiori, and T. Heskes, editors, International Conference on Pattern Recognition in Bioinformatics, pages 419–430, Nijmegen, the Netherlands, 2010. Springer Lecture Notes in Bioinformatics 6282.

textsc Cgal, Computational Geometry Algorithms Library. http://www.cgal.org.

B.A. Chapman and J.T. Chang. Biopython: Python tools for computational biology. ACM SIGBIO Newsletter, pages 15–19, 2000.

F. Chazal, L. Guibas, S. Oudot, and P. Skraba. Persistence-based clustering in Riemannian manifolds. J. ACM, 60(6):1–38, 2013.

Y. Cheng. Mean shift, mode seeking, and clustering. IEEE PAMI, 17(8):790–799, 1995.

A. Chevallier and F. Cazals. Wang-Landau algorithm: an adapted random walk to boost convergence. J. of Computational Physics, 410(1):1–19, 2020.

A. Chevallier, S. Pion, and F. Cazals. Improved polytope volume calculations based on Hamiltonian Monte Carlo with boundary reflections and sweet arithmetics. J. of Computational Geometry, 13(1):55–88, 2022.

John D Chodera and David L Mobley. Entropy-enthalpy compensation: role and ramifications in biomolecular ligand recognition and design. Biophysics, 42:121–142, 2013.

C. Chothia and J. Janin. Principles of protein-protein recognition. Nature, 256:705–708, 1975.

C. Chothia and others. Structural invariants in protein folding. Nature, 254(5498):304–308, 1975.

Michael B Cohen, Yin Tat Lee, Gary Miller, Jakub Pachocki, and Aaron Sidford. Geometric median in nearly linear time. In Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, pages 9–21. ACM, 2016.

T. H. Cormen, C. E. Leiserson, and R. L. Rivest. Introduction to Algorithms. MIT Press, Cambridge, MA, 1990.

T.H. Cormen, C.E. Leiserson, R.L. Rivest, and C. Stein. Introduction to algorithms. MIT press, 2009 (3rd edition).

E. Coutsias, C. Seok, M. Jacobson, and K. Dill. A kinematic view of loop closure. Journal of computational chemistry, 25(4):510–528, 2004.

E. Coutsias, K. Lexa, M. Wester, S. Pollock, and M. Jacobson. Exhaustive conformational sampling of complex fused ring macrocycles using inverse kinematics. Journal of chemical theory and computation, 12(9):4674–4687, 2016.

S. Dasgupta and K. Sinha. Randomized partition trees for exact nearest neighbor search. JMLR: Workshop and Conference Proceedings, 30:1–21, 2013.

A. Sales de Queiroz, G. Sales Santa Cruz, A. Jean-Marie, D. Mazauric, J. Roux, and F. Cazals. Gene prioritization based on random walks with restarts and absorbing states, to define gene sets regulating drug pharmacodynamics from single-cell analyses. PLOS One, 17(11):e0268956, 2022.

C. J. A. Delfinado and H. Edelsbrunner. An incremental algorithm for Betti numbers of simplicial complexes. In Proc. 9th Annu. Sympos. Comput. Geom., pages 232–239, 1993.

F. Despa, D.J. Wales, and S.R. Berry. Archetypal energy landscapes: Dynamical diagnosis. The Journal of chemical physics, 122(2):024103, 2005.

D. Devaurs, T. Siméon, and J. Cortés. Enhancing the transition-based rrt to deal with complex cost spaces. In IEEE International Conference on Robotics and Automation (ICRA), pages 4120–4125. IEEE, 2013.

D. Devaurs, M. Vaisset, T. Siméon, and J. Cortés. A multi-tree approach to compute transition paths on energy landscapes. In Workshop on Artificial Intelligence and Robotics Methods in Computational Biology, AAAI'13, pages pp–8, 2013.

M. do Carmo. Differential Geometry of Curves and Surfaces. Prentice-Hall, 1976.

Jason E Donald, Daniel W Kulp, and William F DeGrado. Salt bridges: geometrically specific, designable interactions. Proteins: Structure, Function, and Bioinformatics, 79(3):898–915, 2011.

S. Dongen. Performance criteria for graph clustering and markov cluster experiments. 2000.

Andreas Döring, David Weese, Tobias Rausch, and Knut Reinert. Seqan an efficient, generic c++ library for sequence analysis. BMC bioinformatics, 9(1):11, 2008.

Jonathan PK Doye and Claire P Massen. Characterizing the network topology of the energy landscapes of atomic clusters. The Journal of chemical physics, 122(8):084105, 2005.

T. Dreyfus, V. Doye, and F. Cazals. Assessing the reconstruction of macro-molecular assemblies with toleranced models. Proteins: structure, function, and bioinformatics, 80(9):2125–2136,

T. Dreyfus, V. Doye, and F. Cazals. Probing a continuum of macro-molecular assembly models with graph templates of sub-complexes. Proteins: structure, function, and bioinformatics, 81(11):2034–2044,

J. Dunitz. Win some, lose some: enthalpy-entropy compensation in weak intermolecular interactions. Chemistry and biology, 2(11):709–712, 1995.

S.R. Eddy. Profile hidden markov models. Bioinformatics, 14(9):755–763, 1998.

H. Edelsbrunner and J. Harer. Computational topology: an introduction. AMS, 2010.

H. Edelsbrunner. Geometry and topology for mesh generation. Cambridge Univ. press., 2001.

Robert C. Edgar. Muscle: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Research, 32(5):1792–1797, 2004.

D. Eisenberg and A.D. McLachlan. Solvation energy in protein folding and binding. Nature, 319:199–203, 1986.

David Eisenberg, Morgan Wesson, and Mason Yamashita. Interpretation of protein folding and binding with atomic solvation parameters. Chem. Scr. A, 29:217–221, 1989.

Geza Fogarasi, Xuefeng Zhou, Patterson W Taylor, and Peter Pulay. The calculation of ab initio molecular geometries: efficient optimization by natural internal coordinates and empirical correction by offset forces. Journal of the American Chemical Society, 114(21):8191–8201, 1992.

R. Forman. Morse theory for cell complexes. Advances in Mathematics, 134:90–145, 1998.

G. Fort, B. Jourdain, E. Kuhn, T. Lelièvre, and G. Stoltz. Convergence of the Wang-Landau algorithm. Mathematics of Computation, 84(295):2297–2327, 2015.

L. Fousse, G. Hanrot, V. Lefèvre, P. Pélissier, and P. Zimmermann. MPFR: A multiple-precision binary floating-point library with correct rounding. ACM Transactions on Mathematical Software (TOMS), 33(2):13, 2007.

Damien Francois, Vincent Wertz, and Michel Verleysen. The concentration of fractional distances. IEEE Trans. on Knowledge and Data Engineering, 19(7):873–886, 2007.

A. Gavezzoti. Molecular aggregation. Oxford, 2007.

M. Gerstein and F.M. Richards. Protein geometry: volumes, areas, and distances. In M. G. Rossmann and E. Arnold, editors, The international tables for crystallography (Vol F, Chap. 22), pages 531–539. Springer, 2001.

D. Goldman, S. Istrail, and C. Papadimitriou. Algorithmic aspects of protein structure similarity. In Foundations of Computer Science, 1999. 40th Annual Symposium on, pages 512–521. IEEE, 1999.

L. Györfi and A. Krzyzak. A distribution-free theory of nonparametric regression. Springer, 2002.

F. Hamprecht, C. Peter, X. Daura, W. Thiel, and W.F. van Gunsteren. A strategy for analysis of (molecular) equilibrium simulations: Configuration space density estimation, clustering, and visualization. The Journal of Chemical Physics, 114(5):2079–2089, 2001.

Sariel Har-Peled. Geometric approximation algorithms. Number 173. American Mathematical Soc., 2011.

L. Hascoet and V. Pascual. The tapenade automatic differentiation tool: principles, model, and specification. ACM Transactions on Mathematical Software (TOMS), 39(3):20, 2013.

HMMER. http://hmmer.org.

H.P. Hratchian and H.B. Schlegel. Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces. Theory and applications of computational chemistry: the first forty years, 4:195–249, 2005.

D.Q. Huynh. Metrics for 3d rotations: Comparison and analysis. Journal of Mathematical Imaging and Vision, 35(2):155–164, 2009.

L. Jaillet, F.J. Corcho, J-J. Pérez, and J. Cortés. Randomized tree construction algorithm to explore energy landscapes. J. Comp. Chem., 32(16):3464–3474, 2011.

J. Janin, R. P. Bahadur, and P. Chakrabarti. Protein-protein interaction and quaternary structure. Quarterly reviews of biophysics, 41(2):133–180, 2008.

Alain Jean-Marie. <a href="https://doi.org/<a href="http://dx.doi.org/10.1145/3150928.3150960">marmoteCore: A Markov modeling platform. In Proceedings of the 11th EAI International Conference on Performance Evaluation Methodologies and Tools, VALUETOOLS 2017, page 60–65, New York, NY, USA, 2017. Association for Computing Machinery.

W. Kabsch and C. Sander. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers: Original Research on Biomolecules, 22(12):2577–2637, 1983.

W. Kabsch. A solution for the best rotation to relate two sets of vectors. Acta Crystallographica Section A, 32(5):922–923, 1976.

L. Käll, A. Krogh, and E. Sonnhammer. A combined transmembrane topology and signal peptide prediction method. Journal of molecular biology, 338(5):1027–1036, 2004. phoebius.

N. Karmarkar. A new polynomial-time algorithm for linear programming. In Proceedings of the sixteenth annual ACM symposium on Theory of computing, pages 302–311. ACM, 1984.

R. M. Karp. Reducibility among combinatorial problems. In Complexity of Computer Computations, pages 85–103, 1972.

K. Karplus, R. Karchin, G. Shackelford, and R. Hughey. Calibrating e-values for hidden markov models using reverse-sequence null models. Bioinformatics, 21(22):4107–4115, 2005.

P.L. Kastritis, J.P.G.L.M. Rodrigues, G.E. Folkers, R. Boelens, and A.M.J.J. Bonvin. Proteins feel more than they see: Fine-tuning of binding affinity by properties of the non-interacting surface. J.M.B., 426:2632–2652, 2014.

A. Krogh, M. Brown, I.S. Mian, K. Sjölander, and D. Haussler. Hidden Markov Models in computational biology: Applications to protein modeling. JMB, 235(5):1501–1531, 1994.

J. Kuffner and S. LaValle. RRT-connect: An efficient approach to single-query path planning. In IEEE International Conference on Robotics and Automation, volume 2, pages 995–1001. IEEE, 2000.

Sandeep Kumar and Ruth Nussinov. Close-range electrostatic interactions in proteins. ChemBioChem, 3(7):604–617, 2002.

D. Landau and K. Binder. A guide to Monte Carlo simulations in statistical physics. Cambridge university press, 2014.

D.P Landau, S-H. Tsai, and M. Exler. A new approach to Monte Carlo simulations in statistical physics: Wang-Landau sampling. American Journal of Physics, 72(10):1294–1302, 2004.

Pierre M Larochelle, Andrew P Murray, and Jorge Angeles. A distance metric for finite sets of rigid-body displacements via the polar decomposition. 2007.

B. Larsen and C. Aone. Fast and effective text mining using linear-time document clustering. In ACM SIGKDD, pages 16–22. ACM, 1999.

J.A. Lee and M. Verleysen. Nonlinear dimensionality reduction. Springer Verlag, 2007.

E. Levina and P. Bickel. The earth mover's distance is the mallows distance: Some insights from statistics. In IEEE ICCV, volume 2, pages 251–256. IEEE, 2001.

Z. Li and H.A. Scheraga. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. PNAS, 84(19):6611–6615, 1987.

J. Lin. Divergence measures based on the Shannon entropy. Information Theory, IEEE Transactions on, 37(1):145–151, 1991.

L. Lo Conte, C. Chothia, and J. Janin. The atomic structure of protein-protein recognition sites. JMB, 285(5):2177–2198, 1999.

S. Loriot and F. Cazals. Modeling Macro-Molecular Interfaces with Intervor. Bioinformatics, 26(7):964–965, 2010.

H. Mahmoud. Evolution of random search trees. Wiley-Interscience, 1992.

N. Malod-Dognin, A. Bansal, and F. Cazals. Characterizing the morphology of protein binding patches. Proteins: structure, function, and bioinformatics, 80(12):2652–2665,

S. Marillet, P. Boudinot, and F. Cazals. High resolution crystal structures leverage protein binding affinity predictions. Proteins: structure, function, and bioinformatics, 1(84):9–20, 2015.

Juliette Martin, Guillaume Letellier, Antoine Marin, Jean-François Taly, Alexandre G de Brevern, and Jean-François Gibrat. Protein secondary structure assignment revisited: a detailed analysis of different assignment methods. BMC structural biology, 5(1):1, 2005.

M. Meila. Comparing clusterings. 2002.

J.W. Milnor. Morse Theory. Princeton University Press, Princeton, NJ, 1963. m-mt-63.

A-Y. Mitrophanov and M. Borodovsky. Statistical significance in biological sequence analysis. Briefings in Bioinformatics, 7(1):2–24, 2006.

M.Oakley, D.J. Wales, and R. Johnston. Energy landscape and global optimization for a frustrated model protein. The Journal of Physical Chemistry B, 115(39):11525–11529, 2011.

G. Monge. Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences de Paris, pages 666–704, 1781.

Francisco Moreno-Seco, Luisa Micó, and Jose Oncina. A modification of the laesa algorithm for approximated k-nn classification. Pattern Recognition Letters, 24(1):47–53, 2003.

M. Muja and D.G. Lowe. Fast approximate nearest neighbors with automatic algorithm configuration. In Int'l Conf. on Comp. vision: Theory and Applications, Lisboa, 2009. Springer.

Naoko Nakagawa and Michel Peyrard. The inherent structure landscape of a protein. Proc Natl Acad Sci U S A, 103(14):5279–5284, Apr 2006.

Jaroslav Nesetril, Eva Milková, and Helena Nesetrilová. Otakar bor r uvka on minimum spanning tree problem (Translation of both the 1926 papers, comments, history). Discrete Mathematics, 233(1):3–36, 2001.

A. Ng, M. Jordan, and Y. Weiss. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems 14: Proceeding of the 2001 Conference, pages 849–856, 2001.

T. O'Donnell and F. Cazals. Enhanced conformational exploration of protein loops using a global parameterization of the backbone geometry. J. Comp. Chem., 44(11):1094–1104, 2023.

T. O'Donnell, C.H. Robert, and F. Cazals. Tripeptide loop closure: a detailed study of reconstructions based on Ramachandran distributions. Proteins: structure, function, and bioinformatics, 90(3):858–868,

T. O'Donnell, V. Agashe, and F. Cazals. Geometric constraints within tripeptides and the existence of tripeptide reconstructions. J. Comp. Chem., 2023.

S. O'Hara and B.A. Draper. Are you using the right approximate nearest neighbor algorithm? In Applications of Computer Vision (WACV), 2013 IEEE Workshop on, pages 9–14. IEEE, 2013.

Patric R.J. Ostergard. A fast algorithm for the maximum clique problem. Discrete Applied Mathematics, 120:197–207, 2002.

J. Parsons, J.B. Holmes, J.M. Rojas, J. Tsai, and C.E.M. Strauss. Practical conversion from torsion space to cartesian space for in silico protein synthesis. Journal of computational chemistry, 26(10):1063–1068, 2005.

W.R. Pearson. Empirical statistical estimates for sequence similarity searches. Journal of molecular biology, 276(1):71–84, 1998.

J. Pérez-Vargas, T. Krey, C. Valansi, Ori O. Avinoam, A. Haouz, M. Jamin, H. Raveh-Barak, B. Podbilewicz, and F. Rey. Structural basis of eukaryotic cell-cell fusion. Cell, 157(2):407–419, 2014.

B. Phipson and G.K. Smyth. Permutation P-values should never be zero: calculating exact P-values when permutations are randomly drawn. Statistical Applications in Genetics and Molecular Biology, 9(1), 2010.

Luca Ponzoni, Guido Polles, Vincenzo Carnevale, and Cristian Micheletti. SPECTRUS: A dimensionality reduction approach for identifying dynamical domains in protein complexes from limited structural datasets. Structure, 23(8):1516–1525, 2015.

J. Porta, L. Ros, F. Thomas, F. Corcho, J. Cantó, and J. Pérez. Complete maps of molecular-loop conformational spaces. Journal of computational chemistry, 28(13):2170–2189, 2007.

Peter Pulay, Geza Fogarasi, Frank Pang, and James E Boggs. Systematic ab initio gradient calculation of molecular geometries, force constants, and dipole moment derivatives. Journal of the American Chemical Society, 101(10):2550–2560, 1979.

N. Radford. MCMC using Hamiltonian Dynamics. In Galin L. Jones Steve Brooks, Andrew Gelman and Xiao-Li Meng, editors, Handbook of Markov Chain Monte Carlo, chapter 5, pages 113–162. Chapman & Hall/CRC, 2012.

F. Richards. The interpretation of protein structures: total volume, group volume distributions and packing density. Journal of molecular biology, 82(1):1–14, 1974.

F. M. Richards. Areas, volumes, packing and protein structure. Ann. Rev. Biophys. Bioeng., 6:151–176, 1977.

D. Ritchie, A. Ghoorah, L. Mavridis, and V. Venkatraman. Fast protein structure alignment using Gaussian overlap scoring of backbone peptide fragment similarity. Bioinformatics, 28(24):3274–3281, 2012.

C. Robert and G. Casella. Monte Carlo statistical methods. Springer Science & Business Media, 2013.

A. Roth, T. Dreyfus, C.H. Robert, and F. Cazals. Hybridizing rapidly growing random trees and basin hopping yields an improved exploration of energy landscapes. J. Comp. Chem., 37(8):739–752, 2016.

Y. Rubner, C. Tomasi, and L.J. Guibas. The earth mover's distance as a metric for image retrieval. International Journal of Computer Vision, 40(2):99–121, 2000.

H. Samet. Foundations of multidimensional and metric data structures. Morgan Kaufmann, 2006.

H Bernhard Schlegel. Estimating the hessian for gradient-type geometry optimizations. Theoretica chimica acta, 66(5):333–340, 1984.

H.B. Schlegel. Exploring potential energy surfaces for chemical reactions: an overview of some practical methods. Journal of computational chemistry, 24(12):1514–1527, 2003.

Robert Schleif. A concise guide to charmm and the analysis of protein structure and function, 2013.

G. Shakhnarovich, T. Darrell, and P. Indyk (Eds). Nearest-Neighbors Methods in Learning and Vision. Theory and Practice. MIT press, 2005.

F. Sievers, A. Wilm, D. Dineen, T.J. Gibson, K. Karplus, W. Li, R. Lopez, H. McWilliam, M. Remmert, J. Söding, J.D. Thompson, and D.G. Higgins. Fast, scalable generation of high-quality protein multiple sequence alignments using clustal omega. Molecular Systems Biology, 7(1), 2011.

Fabian Sievers, Andreas Wilm, David Dineen, Toby J Gibson, Kevin Karplus, Weizhong Li, Rodrigo Lopez, Hamish McWilliam, Michael Remmert, and Johannes Söding. Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Molecular systems biology, 7(1):539, 2011.

M. Simsir, I. Broutin, I. Mus-Veteau, and F. Cazals. Studying dynamics without explicit dynamics: a structure-based study of the export mechanism by AcrB. Proteins: structure, function, and bioinformatics, 89:259–275, 2021.

J. Solomon, F. De Goes, G. Peyré, M. Cuturi, A. Butscher, A. Nguyen, T. Du, and L. Guibas. Convolutional wasserstein distances: Efficient optimal transportation on geometric domains. ACM Transactions on Graphics (TOG), 34(4):66, 2015.

William Stein. Sage for Power Users. Sage, 2012.

Frank H. Stillinger and Thomas A. Weber. Hidden structure in liquids. Phys. Rev. A, 25:978–989, 1982.

A. Strehl and J. Ghosh. Cluster ensembles—a knowledge reuse framework for combining multiple partitions. Journal of machine learning research, 3(Dec):583–617, 2002.

T. Taverner, H. Hernández, M. Sharon, B.T. Ruotolo, D. Matak-Vinkovic, D. Devos, R.B. Russell, and C.V. Robinson. Subunit architecture of intact protein complexes from mass spectrometry and homology modeling. Accounts of chemical research, 41(5):617–627, 2008.

Gareth A Tribello, Michele Ceriotti, and Michele Parrinello. Using sketch-map coordinates to analyze and bias molecular dynamics simulations. Proceedings of the National Academy of Sciences, 109(14):5196–5201, 2012.

J. Tsai, R. Taylor, C. Chothia, and M. Gerstein. The packing density in proteins: standard radii and volumes. JMB, 290:253–266, 1999.

C. Villani. Topics in optimal transportation. Number 58. AMS, 2003.

U. Von Luxburg. A tutorial on spectral clustering. Statistics and Computing, 17(4):395–416, 2007.

D. Wales and J.P.K. Doye. Global optimization by basin-hopping and the lowest energy structures of lennard-jones clusters containing up to 110 atoms. The Journal of Physical Chemistry A, 101(28):5111–5116, 1997.

D. J. Wales, M.A. Miller, and T.R. Walsh. Archetypal energy landscapes. Nature, 394(6695):758–760, 1998.

D. J. Wales. Energy Landscapes. Cambridge University Press, 2003.

F. Wang and D.P. Landau. Efficient, multiple-range random walk algorithm to calculate the density of states. Physical review letters, 86(10):2050, 2001.

T. Wang, B. Li, C. Nelson, and S. Nabavi. Comparative analysis of differential gene expression analysis tools for single-cell rna sequencing data. BMC bioinformatics, 20(1):40, 2019.

Lei Yang, Guang Song, and Robert L Jernigan. Comparisons of experimental and computed protein anisotropic temperature factors. Proteins: Structure, Function, and Bioinformatics, 76(1):164–175, 2009.

Peter N Yianilos. Data structures and algorithms for nearest neighbor search in general metric spaces. In ACM SODA, volume 93, pages 311–321, 1993.