Space_filling_model_shelling_diagram_surface_encoding

Goals: Describing the Morphology of Binding Patches

Shelling a cell complex

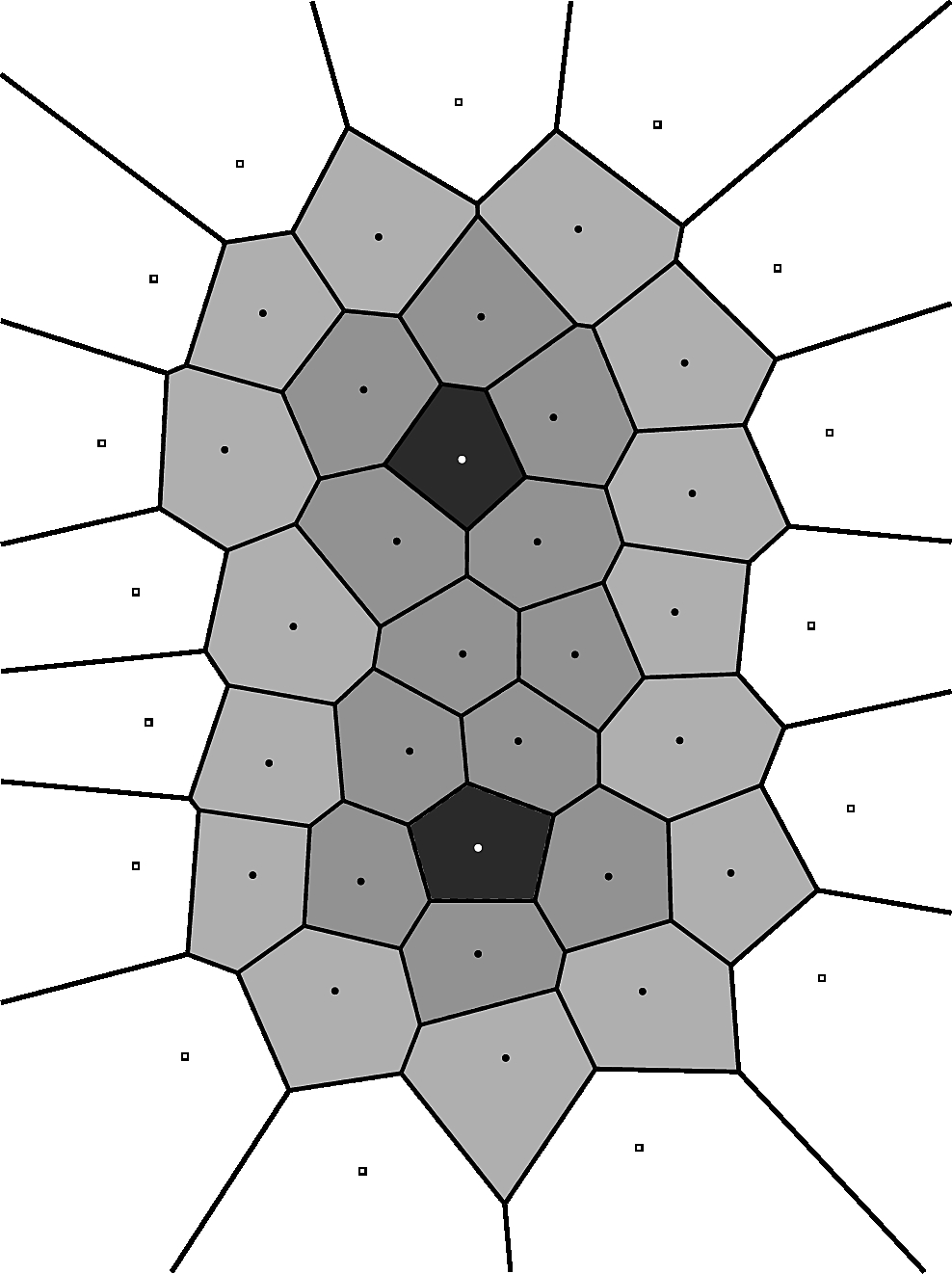
Shelling a cell complex

A Voronoi diagram is an example cell complex, whose cells are the Voronoi cells, two cells being connected by a Voronoi edge. We aim at shelling the cells, by assigning them a number from the outside to the core. Here the background cells are in white, and those being shelled in grey. These latter shells are partitioned in four shells, respectively at distance 1, 2, and 3 from the background. Note that the cells at distance three consist of two connected components. The relative position of the shells is encoded in a tree called a shelling tree.

Binding Patches

Consider a binary complex involving two partners, represented with their solvent accessible models. Given these partners, which typically correspond to a receptor and a ligand, a binding patch or patch for short is the collection of atoms of a given partner that account for key features of the interaction with the second partner. Such atoms can be defined in a number of ways (using a distance threshold or the loss of solvent accessibility in the complex), but Space_filling_model_shelling_diagram_surface_encoding, similarly to Space_filling_model_interface, uses a Voronoi based characterization, as argued in [49] .

The patches contributed by the partners can be used to define the interface, as also explained in Space_filling_model_interface. However, in the sequel, the focus is on the patches, as illustrated below:

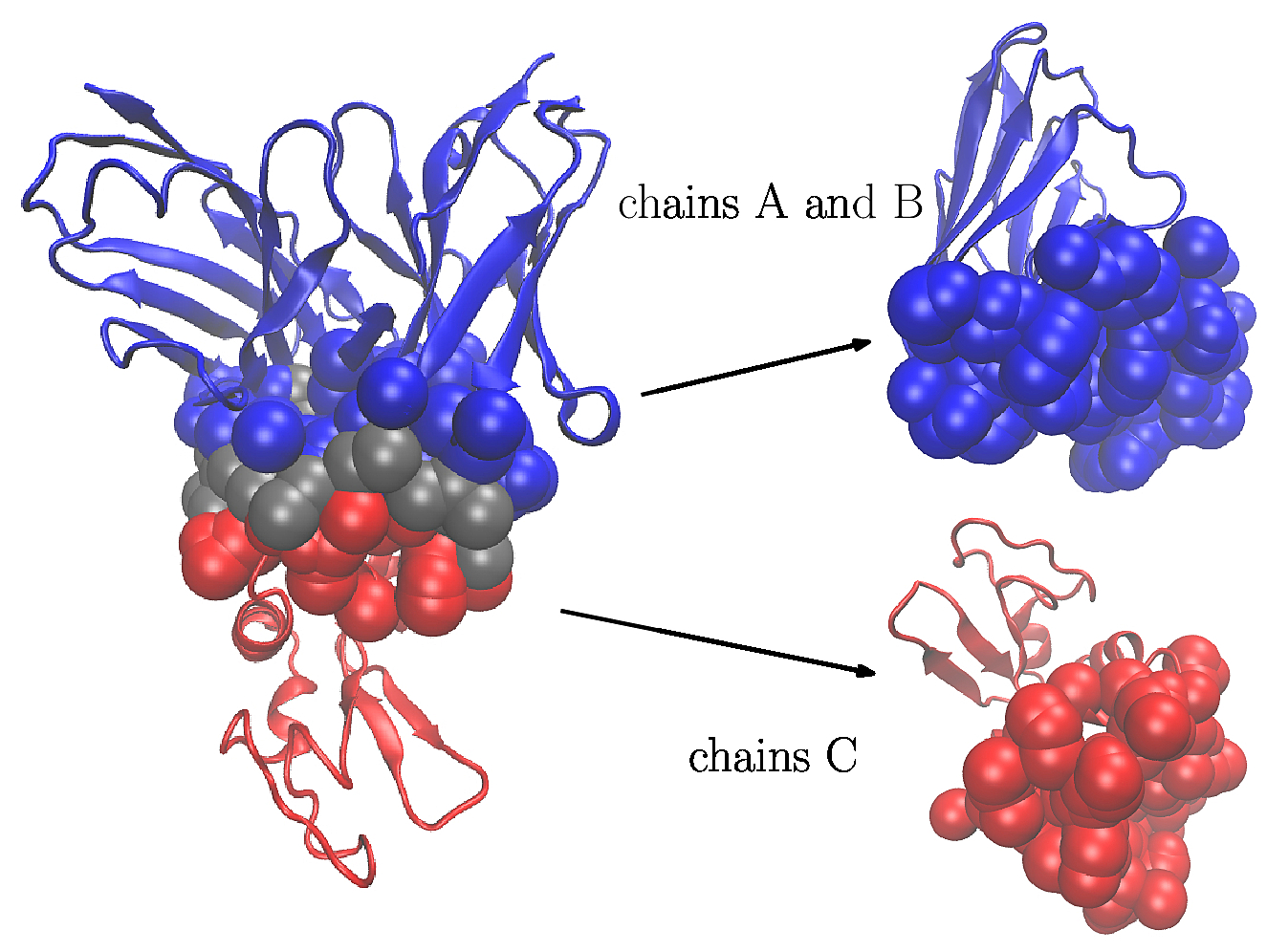Binding patches of a protein complex.

A protein - protein complex involving an antibody (PDB 1vfb, chains A and B in blue) and an antigen (chain C in red). (Left) The two partners with the atoms at the interface represented with the solvent accessible (SAS) model. The interfacial water molecules are represented in gray. (Right) The interface atoms of each partner define its binding patch.

Once a patch has been defined, a classical dissection consists of segregating its atoms into a core and a rim.
As we shall see in section Pre-requisites, Space_filling_model_shelling_diagram_surface_encoding goes beyond the core-rim model by assigning an integer value to each atom, and by grouping such atoms into shells. In a nutshell, the process is as follows:

Let the background atoms of a partner be those which are not involved in its binding patch.

Define the shelling order (SO) of a binding patch atom as the distance from to the nearest background atom (atom is included, so that the SO of an atom located on the boundary of the patch is one).

Let a shell be a group of connected atoms, with the same SO. The atom shelling tree of the binding patch is the tree that encodes the relative position of these atoms, as depicted on Fig. fig-shelling-tree.

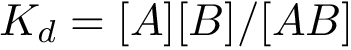
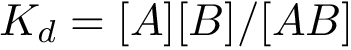
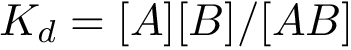
The encoding just defined can be used for a number of structural studies, as detailed in [123] and the references cited therein:

To characterize the morphology of a patch, e.g. by studying the variation of the number of atoms as a function of the SO.

To study the location of amino acids on patches, as a function of their properties (biochemical properties, but also conservation).

To compare patches: as we shall see in Space_filling_model_shelling_diagram_comparison, patches can actually be compared from the geometric or topological standpoints, via their encoding into shelling trees.

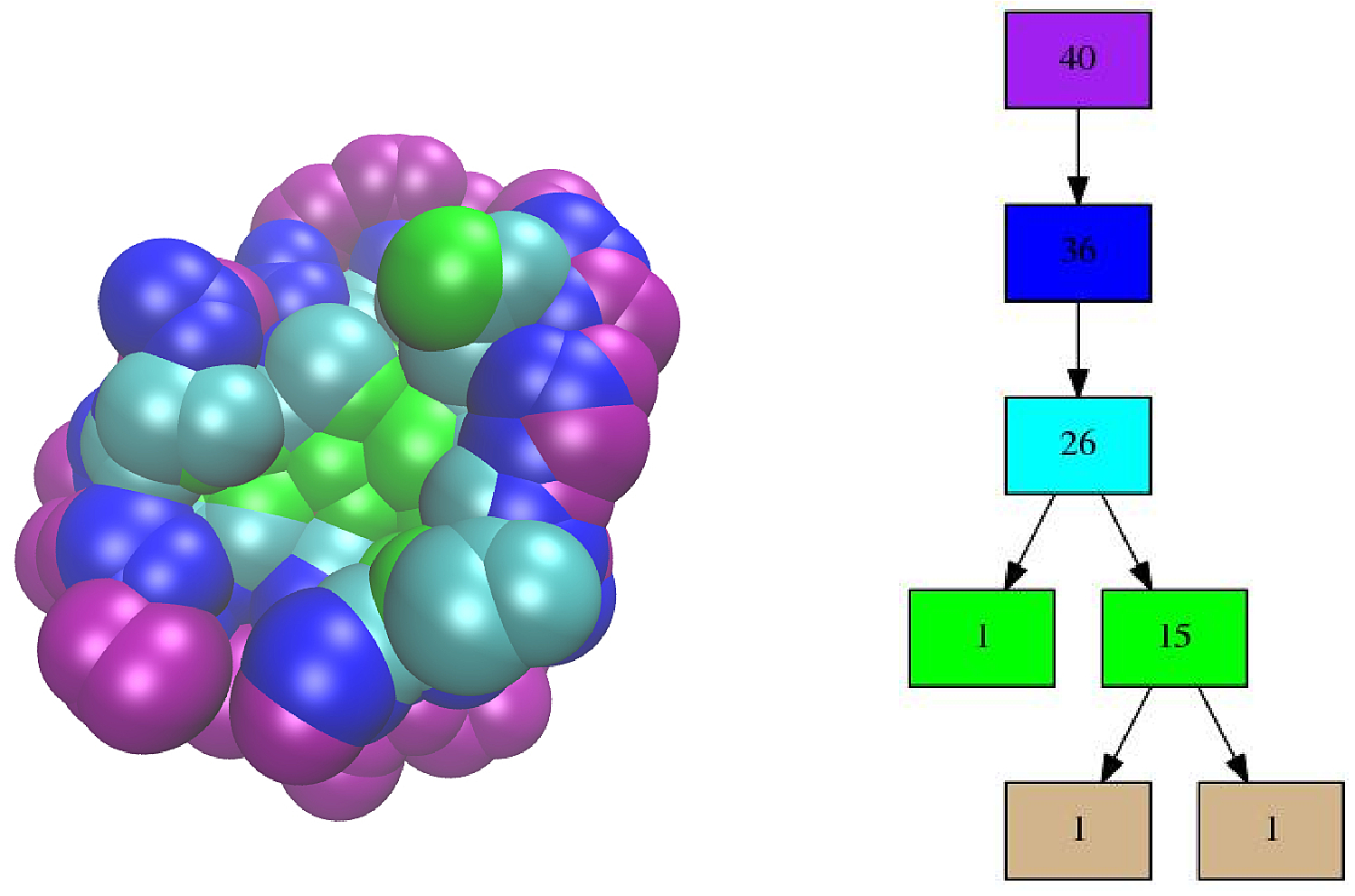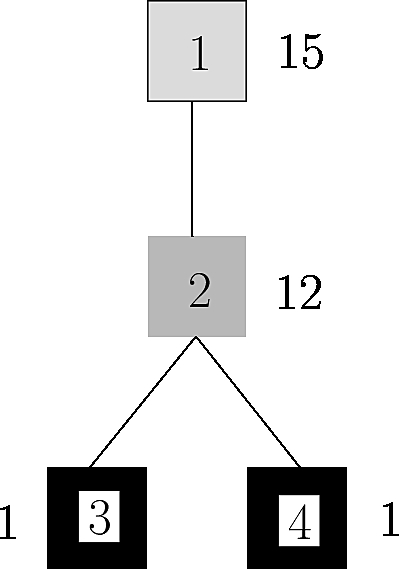
The shelling tree of the binding patch of the IG in the complex of Fig. fig-1vfb-binding-patches.

The binding patch is partitioned into 6 shells: for example, the first one (white atoms), which may be called the rim of the binding patch, consists of 36 atoms located at distance one from the background atoms (grey-blue atoms); the two innermost shells, which are located at distance five from the background, respectively consist of one and two atoms.

Using Vorshell: Shelling Binding Patches at a Binary Interface

This section presents the program 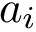$\text{\sblvorshellE}$ .

Pre-requisites

Defining patches

Let and be the two species of the complex, also called partners or subunits, and denote the water molecules that are squeezed in-between them. Let the restriction of a ball be the 3D region defined by the intersection between and its Voronoi region (to be precise, the Voronoi region refers to the region of the ball in the power diagram [26] of the balls of the Solvent Accessible Model). Two atoms are called neighbors provided that their restrictions intersect. A water molecule is called interfacial provided that its has neighbors on both partners. An interface atom is an atom which is neighbor to the other partner's atoms, or to interfacial water molecules.

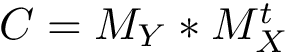
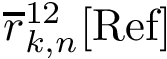
Having identified the interface atoms, we process the two subunits separately, and define:

The binding patch of a subunit is defined as the solvent accessible surface of this partner restricted to its interface atoms. The atoms of a partner that do not belong to the binding patch constitute its background.

A binding patch is a so-called cell complex (Fig. Spherical cell complex) consisting of cells of dimension 0, 1 and 2, respectively: the 0 cells or vertices are points found at the intersection of three spheres; the 1 cells are circle arcs found on the intersection circle of two spheres; the 2 cells or faces are spherical polygons contributed by the atoms. This cell complex is encoded in a so-called Half-edge Data Structure (HDS), that gives access to the incidences between all cells. See the CGAL documentation.

Note that the boundary of a connected component of a binding patch consists of one or more curves made of circle arcs, called connected component of the boundary (CCB) .

Note also that the faces and the circles arcs admit a dual graph, with one vertex per face, and one edge per circle arc. This graph can be used to visit the patch, as we shall see soon.

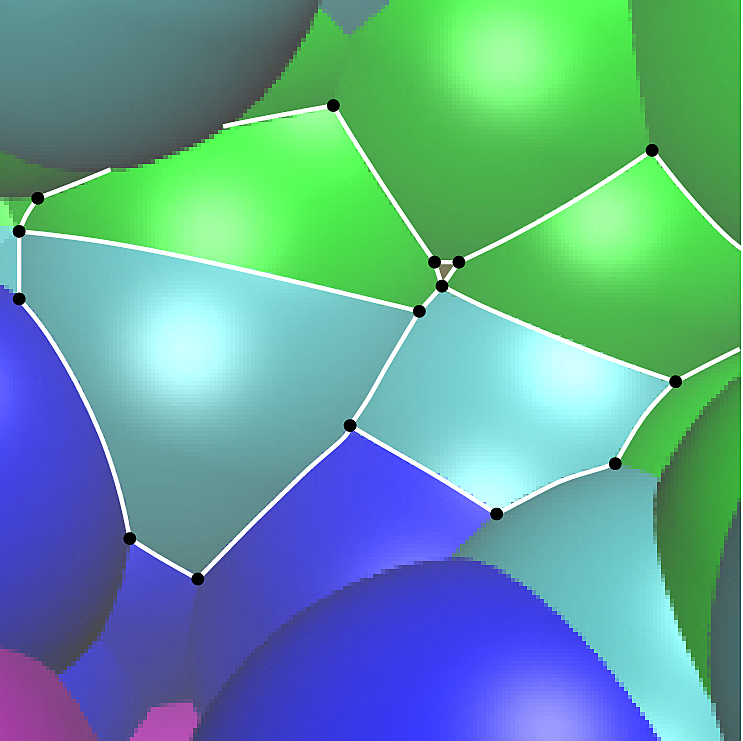It has been shown in [42] that it exits atoms at an interface that are buried within a partner, meaning that they have no accessible surface: such atoms are not represented in a binding patch.

The cell complex defined by the half-edge data structure encoding the boundary of a union of balls.

The cell complex consists of 2-cells (spherical polygons), 1-cells (circle arcs), and 0-cells (points at the intersection of three spheres).

Face Shelling Tree

Shelling consists of assigning an integer value called shelling order or SO to each face (i.e. 2-cell or spherical polygon), and is best presented in terms of graph distance.

More precisely, consider the dual graph of the patch: the nodes of this graph are the faces; two nodes are connected by an edge provided that the associated faces share a circle-arc.

The shelling order or SO of a two dimensional face of the binding patch is its shortest distance to a two dimensional face of the background in the dual graph.

Note that the contribution of an atom to the patch may consist of several faces with different SO.

By convention, the background faces have a SO = 0, so that the SO is a non negative integer, typically in the range 1..10.

The SO and the dual graph are used to compute a following topological encoding, based on shells :

A shell of a binding patch is a maximal connected component of the dual graph involving faces with the same shelling order. The size of a shell is its number of faces. Two shells are called incident provided that there exist faces, on each shell, sharing a circle arc in the patch.

Shells define a partition of the patch, and their relative position is used to define a tree:

The face shelling tree of a patch is the tree defined as follows:

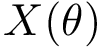
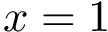
Nodes. Each shell yields a node $\sgnode{s}$ in the tree.
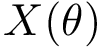
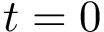
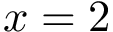
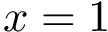
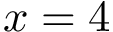
Edges. Consider two incident faces whose SO differ of one unit. Let and be the shells containing these faces, and assume that $\socap{s} + 1 = \socap{t}$ : the face shelling tree contains one arc from $\sgnode{s}$ to $\sgnode{t}$ . The number of outgoing edges of a node is called its arity.

Thus, the face shelling tree merely encodes the relative positions of the shells. It can be converted into an ordered shelling tree by sorting the descendant of a given node by decreasing size.

Atom Shelling Tree

In order to base the comparison of patches on atoms rather than faces, we edit the face shelling tree into an atom shelling tree. The process consists of substituting atoms to faces, with the following special cases:

if an atom is present several times in the same shell, it is counted once;

if an atom belongs to several shells in a branch of the face shelling tree, it is assigned to the shell closest to the root of the tree.

Finally, the sons of a node are sorted by increasing size, i.e. number of atoms, resulting in an ordered atom shelling tree, called shelling tree for short in the sequel.

Note that the atom shelling tree encodes topological information, namely the relative position of the shells, while the 3D coordinates of the atoms within the shells encode the geometry.

Input

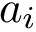
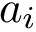
Given the 3D structure of a complex (a .pdb file), and the two sets of chain IDs of the considered partners, $\text{\sblvorshellE}$ generates the atom shelling trees of the two patches. The workflow is presented on Fig. User's workflow. An example run of $\text{\sblvorshellE}$ is given as follows:

> sbl-vorshell-bp-ABW-atomic.exe -f data/1vfb.pdb -P AB -P C --directory results --verbose --output-prefix --log --is-tree --patch-viewer vmd

The main options of the program $\text{\sblvorshellE}$ are:
-f string: PDB file of the input molecule
-P string: specifiation of the chains of one partner (use it twice for both partners)
–patch-viewer string(=none): create a file for visualizing the binding patches and their shelling with vmd or pymol

Note that a default radius of $1.4 \AA$ is added to all atoms to define the Solvent Accessible Model of the input molecule.

File Name

Description

1vfb pdb file

Immunoglobulin-antigen complex

Input files for the run described in section Input .

Output

Three categories of output files are created from the last command line:

two xml files representing the atom shelling trees for partner A and for partner B.

two input files for Graphviz (see section Graphviz (Graph visualization)) so as to visualize the atom shelling trees. For the cases where Graphviz is not installed, the option –eps-format tells the program to also dump encapsulated postscript (eps) files.

a vmd file to inspect the shells of the two atom shelling trees. Note that two pdb files are generated, each of them containing all the atoms of the binding patches of each partner. To load these vmd files, the {fastload} plugin available from the aforementioned web site is highly recommended.

During its execution, a record on the main steps undertaken is dumped into the called window. This information can be sent stored a log file with the option -l .

Preview	File Name	Description
General: log file
	Log file	Log file containing high level information on the run of $\text{\sblvorshellE}$
Module shelling of patch at interface: patches, face shelling trees and atom shelling trees
	A Atom Shelling Forest xml file	XML file describing the Atom Shelling Forest of binding patches of partner A
	A Atom Shelling Forest dot file	dot file to be used with Graphviz for visualizing the Atom Shelling Forest of binding patches of partner A
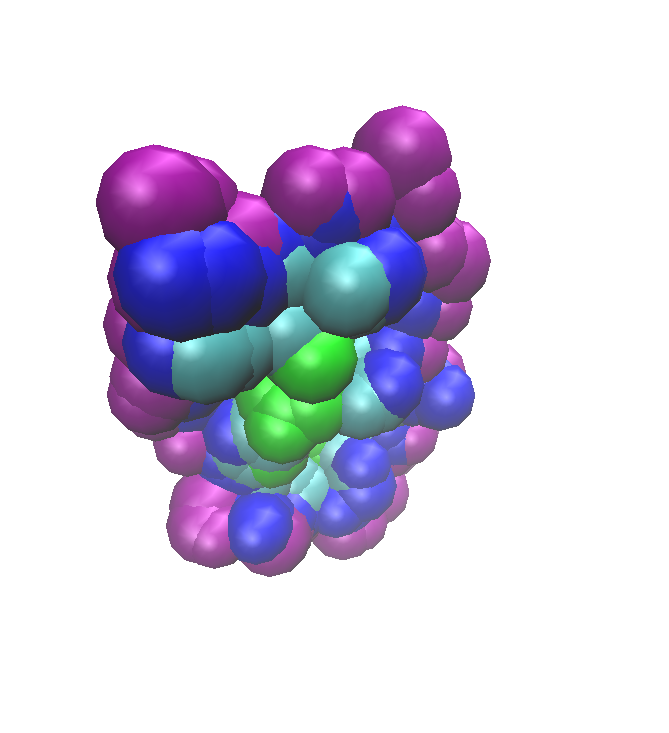	A Binding Patches VMD file	Visualization state file of the binding patches of partner A colored by shelling orders
	B Atom Shelling Forest xml file	XML file describing the Atom Shelling Forest of binding patches of partner B
	B Atom Shelling Forest dot file	dot file to be used with Graphviz for visualizing the Atom Shelling Forest of binding patches of partner B
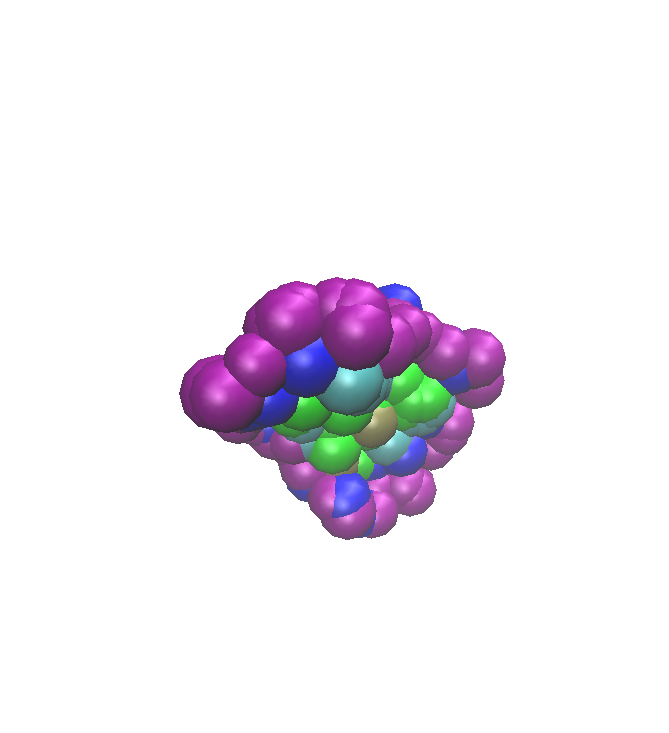	B Binding Patches VMD file	Visualization state file of the binding patches of partner B colored by shelling orders

Output files for the run described in section Input, classified by modules – see Fig. fig-vorshell-workflow .

For visualizing the shelling forests, we recommend you to install Graphviz (see the Graphviz web site), and using the dot software for drawing the graph from a .dot file. Note that there are other software from the Graphviz library for drawing the graphs with different embedding.

For visualizing the particles with their shelling orders, we recommend you to install VMD (see the VMD web site): first load the input PDB file, then load the output visualization state files. The loading of visualization state files may be long, but is a lot faster using the fastload VMD script delivered with the library (in the scripts/vmd directory).

Visualization, Plugins, GUIs

The SBL provides VMD and PyMOL plugins to use the programs of Space_filling_model_shelling_diagram_surface_encoding . The plugins are accessible in the Extensions menu of VMD or in the Plugin menu of PyMOL . Upon termination of a calculation launched by the plugin, the following visualizations are available:

for each partner, the selection of atoms within shells, for each shelling order,
for each partner, the circle arcs bounding the patches.

Programmer's Workflow

The programs of Space_filling_model_shelling_diagram_surface_encoding described above are based upon generic C++ classes, so that additional versions can easily be developed.

In order to derive such versions, there are two important ingredients, that are the workflow class, and its traits class.

The Traits Class

T_Space_filling_model_shelling_diagram_surface_encoding_traits:

The Workflow Class

T_Space_filling_model_shelling_diagram_surface_encoding_workflow:

Table of Contents