 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: F. Cazals and T. Dreyfus and N. Malod-Dognin

A binding patch (patch for short) of a molecular model is a set of atoms involved in an interaction with a partner in a complex, as defined in the applications of Space_filling_model_shelling_diagram_surface_encoding.
The classical way to compare two patches 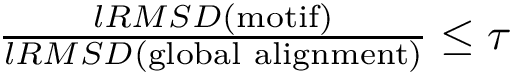
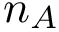
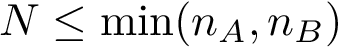
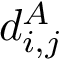

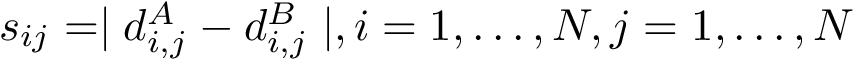

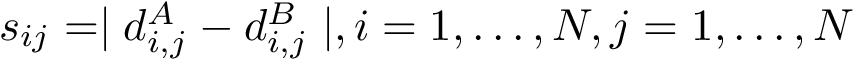
This approach has two main limitations:
Space_filling_model_shelling_diagram_comparison gets around these two difficulties by proposing structural comparisons favoring either geometric or topological features, as illustrated on Fig. fig-lego-interface-flat-curved-montage.
To present them, recall that Space_filling_model_shelling_diagram_surface_encoding computes a topological encoding of binding patches, by aggregating the atoms of a binding patch into shells, a shell being a collection of neighboring atoms located at a fixed distance of the binding patch boundary. The relative position of these shells yields an encoding of the patch as an ordered tree known as the atom shelling tree, see Fig. fig-shelling-tree.
The fact that the tree is ordered is important: using dynamic programming, ordered trees can be compared via a simple operation known as the Tree Edit Distance (TED) [24] . In a nutshell, the algorithm for TED is a generic algorithm computing the cost of morphing a tree 
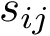
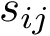
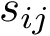
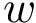
Interestingly, adjusting the semantics of the three aforementioned operations allows defining two types of TED calculations:
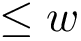

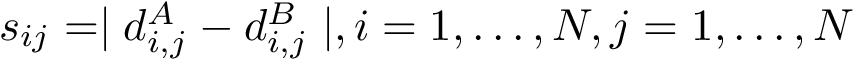
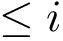

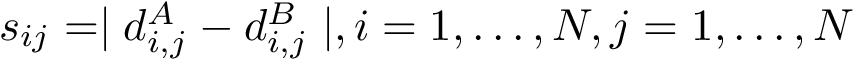
Notations For both the intersection 
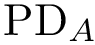
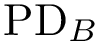
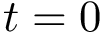
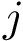
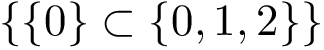
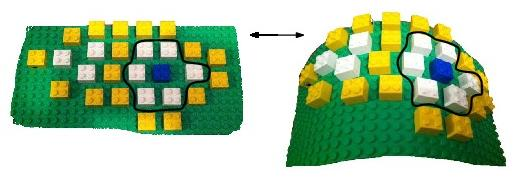 |
An idealized illustration of the topological rigidity handled in Space_filling_model_shelling_diagram_comparison For the sake of illustration, a fictitious binding patch is presented, each lego block meant to represent one atom. The color coding of the atoms codes the shelling order of the patch, as defined in Space_filling_model_shelling_diagram_surface_encoding. From left to right, the binding patch bends: while the relative position of the atoms in 3D changes, each particular atom retains exactly the same neighbors, which we illustrate with the blue atom. Such a binding patch is termed geometrically flexible, but topologically rigid. Space_filling_model_shelling_diagram_comparison provides methods to assess the rigidity / flexibility of binding patches, either from a geometric or topological standpoint. |
This section presents the program 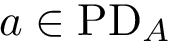
Isotopology. A shell 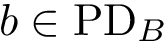
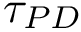
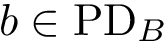
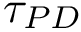
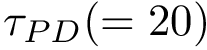
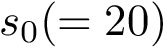
(i) 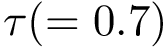
(ii) 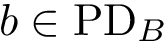
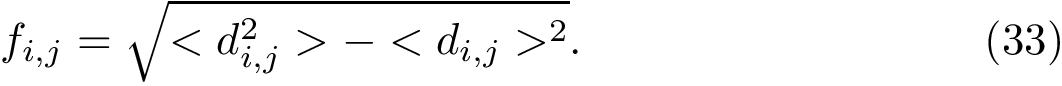
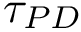
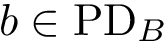
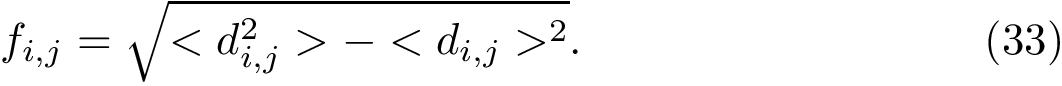
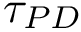
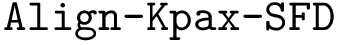
Two atoms of 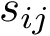
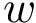
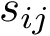
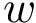
Problem statement. The comparison problem reduces to an ordered Tree Edit Distance problem (TED) having the following edition costs.
Adding or deleting a shell 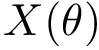
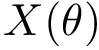
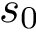
.
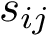
Denoting 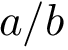
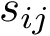
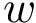
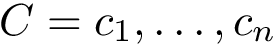
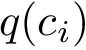
.
The similarity between two trees is then the number of their isotopologic atoms normalized by the size of the two trees to be in [0,1]:
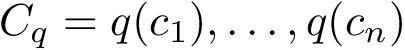
Quasi-isometry. Given two shelling trees 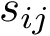
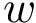
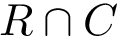
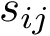
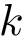
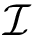
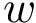
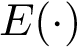
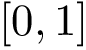
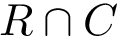
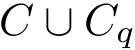
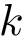
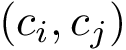
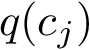
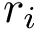
Between 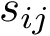
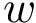
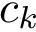
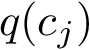
Problem statement.
To favor geometric comparisons, we are interested in finding the largest subset of atoms between 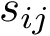
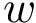
Mimicking Eq. eq-sim-tedt, the similarity between 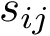
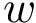
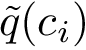
It can be shown that the previous calculation reduces to a maximum clique calculation [39] .
To strike a balance between geometric and topological criteria, we are interested in finding the subsets of atoms that are isotopologic and where the quasi-isometric constraints are satisfied between the matched shells. Meeting these criteria is amenable to a TED calculation, using the following costs.
The costs for inserting/deleting a shell 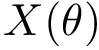
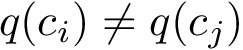
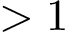
Problem statement.
To balance topological and geometric comparisons, we are interested in finding the largest subset of atoms between 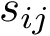
Let 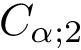
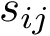
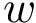
In this case, 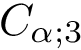
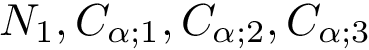
.
The similarity between two trees is then the size of 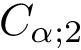
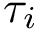
Given the computational complexity of purely geometric comparisons, we focus in the sequel on the topological and mixed comparisons.
Both methods respect the isotopologic constraints, but only Clique respects all the isometric constraints. 
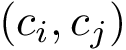
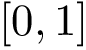
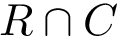
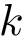
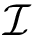
This implies that the size of the atomic subsets returned by Clique are smaller than the size of the subsets returned by 
Thus, the following holds:
Also, because of the possibly broken isometric constraints, 
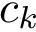
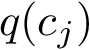
This section describes the application's options and file formats.
Given the atom shelling trees of two binding patches (XML file format), 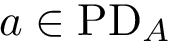
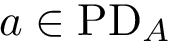
> sbl-compatch.exe --shelling-forest data/1vfb_atom_shelling_tree_A.xml --shelling-forest data/1vfb_atom_shelling_tree_B.xml --comparison-mode g --directory results --verbose --output-prefix --log
| File Name | Description |
| Source Atom Shelling Forest xml file | Atom shelling tree of the binding patch of the partner A of the IGAg complex 1vfb |
| Target Atom Shelling Forest xml file | Atom shelling tree of the binding patch of the partner B of the IGAg complex 1vfb |
There are two output files that are created from the last command line:
During its execution, a record on the main steps undertaken is dumped into the called window. This information can be sent stored a log file with the option -l .
| Preview | File Name | Description |
| General: log file | ||
| Log file | Log file containing high level information on the run of | |
| Module shelling forests comparison | ||
| Comparison xml file | XML file describing how to move from the source tree to the target tree | |
 | Comparison dot file | dot file for visualizing the matching between the two input trees using GraphViz |
For visualizing the shelling forests comparison, we recommend you to install Graphviz (see the Graphviz web site), and using the dot software for drawing the graph from a .dot file. Note that there are other software from the Graphviz library for drawing the graphs with different embedding.
The computation of isotopologic atom sets reduces to the classical TED, see [24] , with the insertion / deletion / morphing costs discussed above.
The computation of quasi-isometric subsets of atoms is rephrased as a maximum clique problem as follows. Let 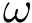
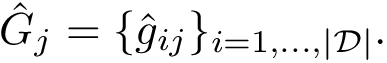
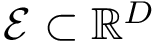
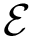

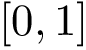
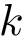
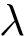
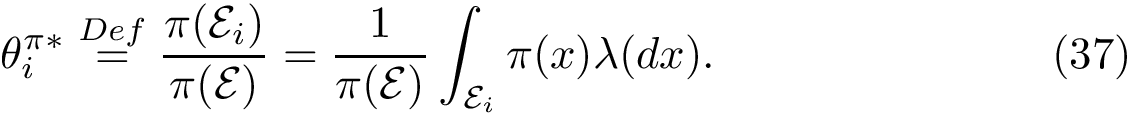
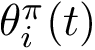
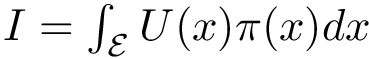
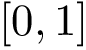
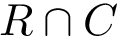
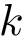
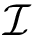
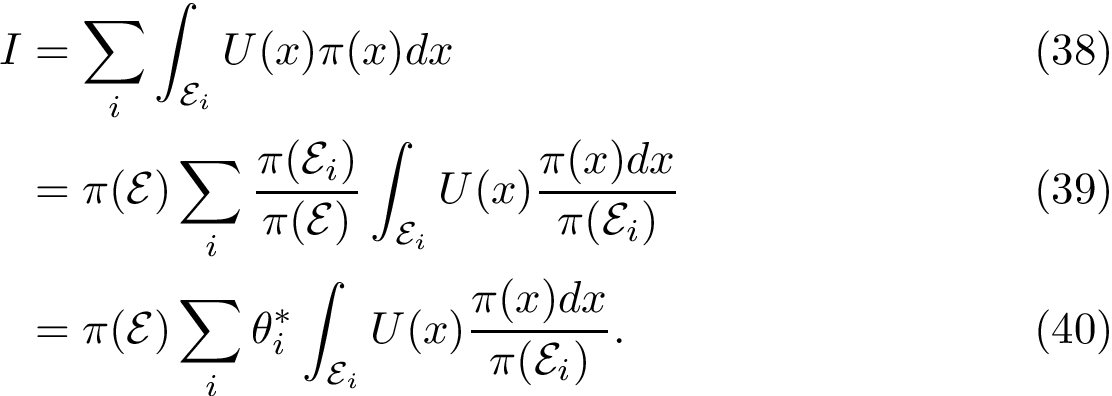
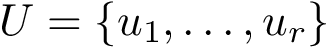
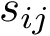

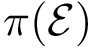
The maximum clique problem is NP-Hard [116] , and is solved by using Ostergard's algorithm [151] . Note that the isotopology constraints reduce the number of edges in 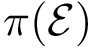
The applications of Space_filling_model_shelling_diagram_comparison described above are based upon generic C++ classes, so that additional versions can easily be developed.
In order to derive such versions, there are two important ingredients, that are the workflow class, and its traits class.
T_Space_filling_model_shelling_diagram_comparison_traits:
T_Space_filling_model_shelling_diagram_comparison_workflow: