 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
|
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: F. Cazals and T. Dreyfus and C. Roth
This package provides various methods to analyze sampled energy landscapes, with in particular various statistics on its transition and connectivity graphs.
We have seen in the package Transition_graph_of_energy_landscape_builders that there are three options to build a transition graph (see def. def-transition-graph):
In the following, we exploit such transition graphs, to ultimately gain insights on the structure and dynamics of molecular systems, see [173] and [67] . In this perspective, this package proposes various methods to characterize sampled energy landscapes.
The following functionalities are provided on transition graphs and disconnectivity graphs (see def. def-DG):
Transition graph
Transition graph: Morse based analysis, including persistence analysis for local minima and distribution of barriers' heights.
Disconnectivity graphs: computation of morphological properties (internal path length),
These functionalities are available in the programs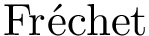 
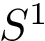
and 
.
A variety of algorithms can be used to explore energy landscapes, and their results can be turned into a compressed transition graph – definition def-transition-graph, using e.g. methods presented in the package Transition_graph_of_energy_landscape_builders.
In the sequel, we are interested in topological and geometric information characterizing such graphs.
Topological information. For a given graph, the number of connected components and the number of cycles in this graph are known as the first and second Betti numbers [79] , and are respectively denoted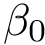 
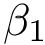
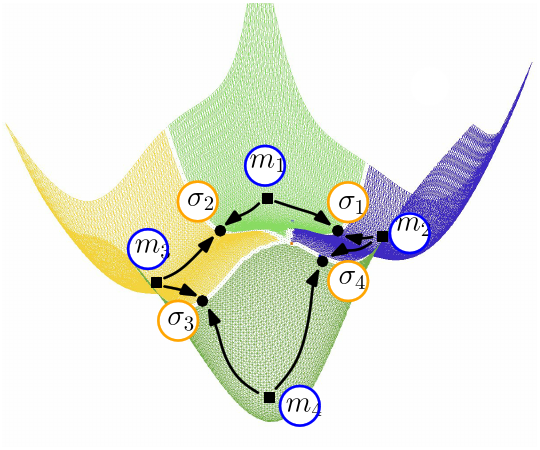
and 
. We report them for the transition graph, and we also compute statistics on a per connected component basis.
The presence of cycles in a transition graph is especially interesting, since such cycles correspond to different paths connecting the same local minima. Cycles involving two edges are also of interest, as they may arise in two situations. The first corresponds to the situation in which a loop around a saddle is anchored in a single local minimum (Fig. fig-bump-middle-slope-bassin). The second is due to post-sampling processing techniques that may be used to group minima. For instance, in the BLN model, enantiomeric left and right handed helices may be considered as identical in certain contexts; identifying them as such results in the creation of a cycle.
Geometric information. Assume a distance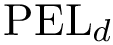 
between conformation has been chosen. The simplest geometric information embodied in a transition graph is the length of its edges, and can be assessed with the statistical summary of Eq. (eq-stat-triple-edge-lengths).
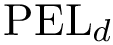
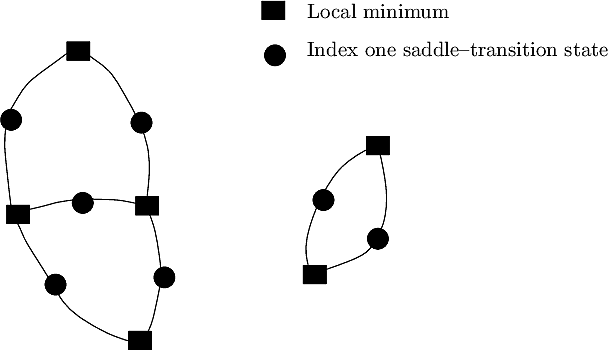In particular, the presence of long edges hints at challenging landscapes: even when the between all pairs of local minima is small, one may have to follow a long valley to reach a saddle connecting two minima.
 |
| Describing the topology of a transition graph with the first and second Betti numbers This fictitious examples features a TG with two connected components: the first one involves four local minima and five saddles; the second one involves two local minima and two saddles. The Betti numbers are:  (two connected components) and  (three cycles). |
 |
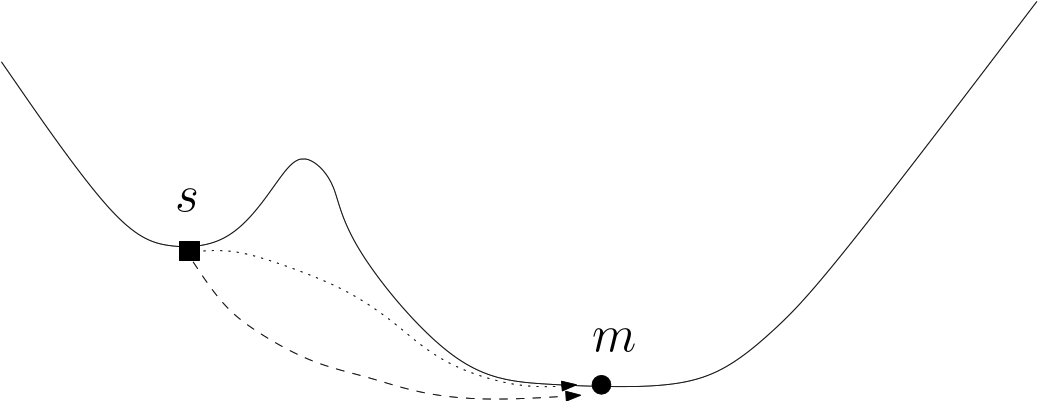A loop around a saddle  may be anchored in a single local minimum  — a.k.a bump transitionNote that the dotted path is located behind the bump of this fictitious 2D landscape. |
Consider a transition graph, and assume that selected minima called landmarks have been singled out. For example, one may select the lowest local minima or the most persistent ones (package Morse_theory_based_analyzer).
For a given landmark, the distribution of distances from that landmark to its connected saddles provides an estimate on the size of the basin of that landmark [74] . Also, a large value for the smallest such distance provides information on the distance to be traveled to escape from the basin of that minimum. Similarly, the relative position of all landmarks is assessed by the statistical summary of all pairwise distances.
Morse theory and topological persistence provide a number of concepts and tools which are highly relevant to study energy landscapes. We describe a few of them in the sequel, and refer the reader to the terminology section Terminology and Concepts for a quick recap on central notions such as sublevel set, key saddle, Morse-Smale-Witten complex.
Of particular interest is the pairing between local minima and their key saddles (see def. def-key-saddle). This pairing, and more specifically the elevation drop between the key saddle and its minimum indeed defines the barrier height. The elevation of the minimum of that of its key saddle may also be seen as the birth date and the death date of the catchment basin of the local minimum: when scanning the landscape with a horizontal plane, the basin appears at the elevation of the local minimum, and disappears i.e. merges with another basin at the elevation of its key saddle. Putting together all points (birth date, death date) defines the so-called persistence diagram (PD), as detailed in the package Morse_theory_based_analyzer.
Persistence diagrams for sublevel sets. The analysis presented above for local maxima and super level sets applies directly for local minima and sublevel sets, yielding a persistence diagram whose points code local minima of the height field. The executive summary concerning the PD of a landscape goes as follows:
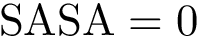
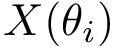
By construction, the lowest local minimum is not paired with any saddle. That is, if the height field has local minima, its PD contains 
points.
A point of the PD corresponds to a pairing involving one local minimum and one saddle. Mathematically, these points are critical points of the height field: the minimum is an index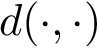 
c.p. (its Hessian has zero negative eigenvalues), while the saddle is an index one c.p. (its Hessian has one negative eigenvalue).
All points of the PD are above the diagonal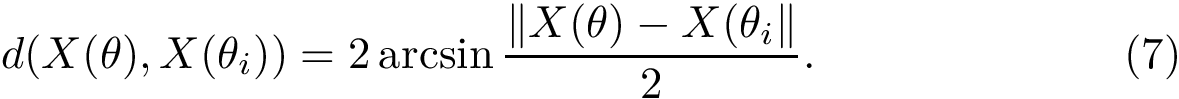 
, and the distance from a point to the diagonal is a measure of the stability of the corresponding local minimum.
The disconnectivity graph (DG) of a landscape describes the merge events of catchment basins, which occur at key saddles (see also def. def-DG).
The generic situation expected in a DG is that of a binary merge, namely a saddle is linked to two local minima. (Degenerate situations may occur, though: for example, a monkey saddle is linked to three local minima.) That is a generic DG is a binary tree: each internal node representing a saddle is associated with at most two children, and each leaf represents a local minimum.
The morphology of a complete binary tree can vary between that of a path (in which one child of each internal node is a leaf and the other is an internal node) and that of a perfectly balanced tree (in which each internal node has two children i.e. subtrees of the same size). To assess the structure of such trees, we use the so-called external path length (EPL) [122] . Defining the depth of a node as the number of edges required to reach it from the root, the EPL is the sum of depths of the leaves of the tree. Likewise, the internal path length (IPL) is the sum of the depth of internal nodes. If 
is the number of internal nodes (index one saddles in our case), the EPL when the tree is a path is 
, which we will write using the shorthand 
, while that of a perfectly balanced tree is 
. Since the latter, symmetrical tree is not a realistic reference, we use instead the EPL of a random binary search tree [122] , which is asymptotically equivalent to 
.
 |
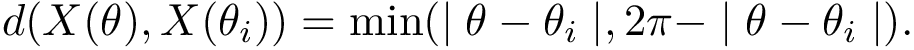
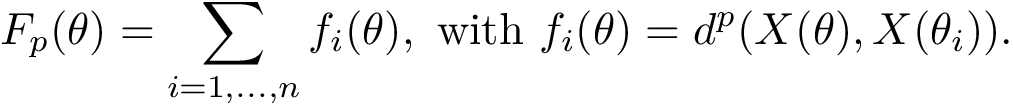
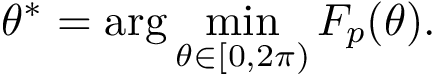
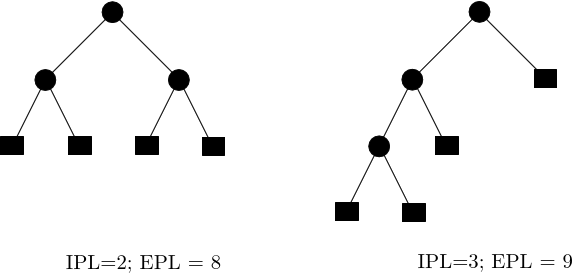| Internal and external path lengths of binary trees (IPL and EPL) The IPL counts the number of edges traversed, from the root, to reach internal nodes (disks); in the context of disconnectivity graphs for energy landscapes, recall that these refer to key saddles. The EPL counts the number of edges traversed to reach the leaves of the tree; in the context of DG, these refer to local minima. |
Main options.
are:–transition-graph string: xml file representing the compressed transition graph of a sampled energy landscape–topology: run topology analysis over the uncompressed transition graph–Morse: run Morse theory based analysis over the uncompressed transition graph with the potential energy as Morse function–skip-saddle-SM: When performing persistence based simplification, do not report the stable manifold of saddle points–landmarks: run shortest paths analysis through input landmark vertices on the compressed transition graph–landmarks-filename string: file listing the landmark indices in the compressed transition graph
Input.
The main input is a transition graph of a sampled energy landscape, produced by the programs of the application Transition_graph_of_energy_landscape_builders as XML archives. If shortest paths with landmarks are desired, it is required to load a file listing the vertices of the input transition graph that are the landmarks. A strategy for producing a landmarks file consists on comparing the input transition graph with a reference transition graph containing only reference conformations. Programs of the application Energy_landscape_comparison produce a Graphviz file showing the correspondence between the vertices of two input transition graphs. This allows to visually select the vertices of an input graph that will be landmarks.
Main output.
Identical to those obtained when building the transition graph see Main specifications, yet possibly corresponding to a different persistence threshold:
index (integer) inf (keyword) elevation (floating point number)
Optional output.
Main options.
are:–transition-graph string: xml file representing the compressed transition graph of a sampled energy landscape–topology: run topology analysis over the uncompressed transition graph–Morse: run Morse theory based analysis over the uncompressed transition graph with the potential energy as Morse function–skip-saddle-SM: When performing persistence based simplification, do not report the stable manifold of saddle points
Input. See section above.
Main output. See section above.
Computing the first and second Betti number of a graph respectively require running a traversal of the graph and a union-find algorithm [79], [61] .
Computing the distances between landmarks can be done using a variant of Dijkstra's shortest path algorithm, where one walks on the graph provided, but records and relaxes distances between landmarks only [61] .
The programs of Energy_landscape_analysis described above are based upon generic C++ classes, so that additional versions can easily be developed.
In order to derive other versions, there are two important ingredients, that are the workflow class, and its traits class.
T_Energy_landscape_analysis_traits:
T_Energy_landscape_analysis_interface_workflow:
This package provides also the program sbl-energy-landscape-analysis-graph-star.exe, allowing to select/extract/perform statistics on the star of a vertex in a weighted graph.
See the following jupyter notebook:
We have seen in the package Transition_graph_of_energy_landscape_builders that there are three options to build a transitio graph:
In the following, we exploit such transition, as explained in the User manual.
from SBL import SBL_pytools
from SBL_pytools import SBL_pytools as sblpyt
help(sblpyt)
The options of the analyze method in the next cell are:
import re #regular expressions
import sys #misc system
import os
import pdb
import shutil # python 3 only
from IPython.display import Image
from IPython.display import IFrame
def analyze_transition_graph(metric, transGraph, landmarks = None, topology = True, Morse = True):
odir = "tmp-results-%s" % metric
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
# check executable exists and is visible
exe = shutil.which("sbl-energy-landscape-analysis-%s.exe" % metric)
if not exe:
print("Executable not found")
return
print(("Using executable %s\n" % exe))
cmd = "sbl-energy-landscape-analysis-%s.exe --transition-graph %s \
--directory %s --verbose --log " % (metric, transGraph, odir)
if landmarks:
cmd += "--landmarks --landmarks-filename %s " % landmarks
if topology:
cmd += "--topology "
if Morse:
cmd += "--Morse "
print(("Executing %s\n" % cmd))
os.system(cmd)
cmd = "ls %s" % odir
ofnames = os.popen(cmd).readlines()
print(("All output files in %s:" % odir),ofnames,"\n")
sblpyt.show_log_file(odir)
The Himmelblau function is defined by the bivariate polynomial $f(x,y) = (x^2+y-11)^2 + (x+y^2-7)^2$.
from IPython.display import Image
Image(filename='fig/himmelblau-matlab-cropped.png')
print("Marker : Calculation Started")
analyze_transition_graph("euclid", "data/himmelbleau_tg.xml", landmarks = "data/himmelbleau_landmarks.txt")
print("Marker : Calculation Ended")
## We can now easily visualize the main plots i.e. the disconnectivity forest and the persistence diagram
odir = "tmp-results-euclid"
images = []
images.append( sblpyt.find_and_convert("disconnectivity_forest.eps", odir, 100) )
images.append( sblpyt.find_and_convert("persistence_diagram.pdf", odir, 100) )
sblpyt.show_row_n_images(images, 100)
Recall that BLN69 is a toy protein model made of 69 pseudo-amino acids which are either hydrophoBic, hydrophiLic,or Neutral:
from IPython.display import Image
Image(filename='fig/bln69-visu7305.jpg')
print("Marker : Calculation Started")
#analyze("euclid", "data/bln69_transition_graph.xml", landmarks = "data/bln69_transition_graph.xml")
analyze_transition_graph("lrmsd", "data/bln69_transition_graph.xml", landmarks = "data/bln69_landmarks.txt")
print("Marker : Calculation Ended")
odir = "tmp-results-lrmsd"
images = []
images.append( sblpyt.find_and_convert("disconnectivity_forest.eps", odir, 100) )
images.append( sblpyt.find_and_convert("persistence_diagram.pdf", odir, 100) )
sblpyt.show_row_n_images(images, 100)
1.9.1