Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Table of Contents

Authors: F. Cazals and T. Dreyfus and C. Roth

Conformational_ensemble_analysis

This package provides methods to assess the conformational diversity of an ensemble of conformations.

Goals

Consider a sampling – aka conformational ensemble, as defined in section Conformational ensembles – aka samplings. This package offers functionalities to:

  • Assessing the structural diversity of the sampling, using various statistics:

    • the atomic fluctuations (root mean square fluctuation, RMSF)
    • statistics on the edges of a spanning tree connecting the conformations.

  • Perform a hierarchical clustering of the conformations.

  • Computing pairwise distances between (selected) conformations, so as e.g. to run a dimensionality reduction algorithm such as multi-dimensional scaling or Isomap.

These functionalities are provided in the program $\sblCEAL$.

Using sbl-conf-ensemble-analysis-lrmsd.exe

Pre-requisites

Sampling diversity

Currently we use two measures for the sampling diversity, in order to assess the extent to which a molecule deforms within an ensemble 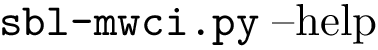$C = \{ c_1,\dots, c_n\}$. Assume that all conformations have been aligned in the same coordinate system, see Eq. eq-aligned-conformations.

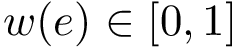
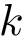
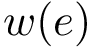
The first is the standard method for estimating the root-mean squared atom fluctuations ( $\rmsf$). Denoting $\average{\atomi{\tilde{c}}{k}}$ the average position of the $k$-th atom in the aligned samples $\tilde{C}$. The $\rmsf$ of the $k$-th atom is defined by

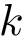
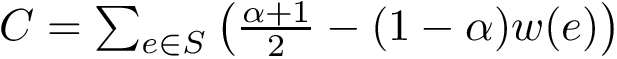
$ RMSF_k = \sqrt{\frac{1}{n} \sum_{i=1,\dots,n} \vvnorm{\atomi{\tilde{c_i}}{k}\ -\ \average{\atomi{\tilde{c}}{k}}}^2. } $

The second measure is the bounding box (in Cartesian coordinates) of the ensemble 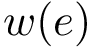$\tilde{C}$ of aligned structures.

Sampling sparsity via spanning trees

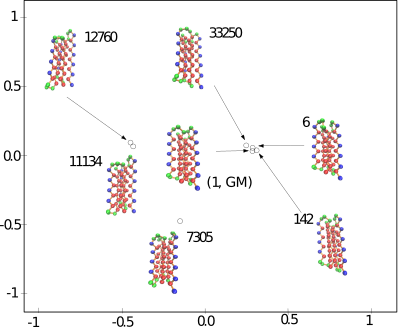
A conformational ensemble may contain clusters , i.e. groups of conformations such that pairwise distances within a cluster are smaller than distances between conformations across clusters. We investigate such properties using graphs.

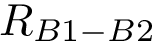
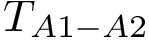
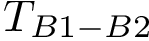
Assume that a connected nearest neighbor graph (NNG, see Def. def-nng) $G$ has been built over the samples, and denote $\VSet{G}$ (resp. $\ESet{G}$) its vertex set (resp. its edge set). Assume that to each edge $e={c_i,c_j}\in \ESet{G}$ is attached the quantity $\dCalC{c_i}{c_j}$. We compute a minimum spanning tree $\MST{G}$ of $G$. If the conformational ensemble contains $n$ conformations, this tree involves $n-1$ edges. 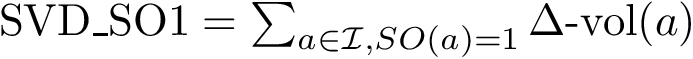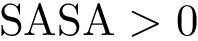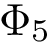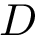For an edge $e={c_i, c_j}$ of this graph, the edge length is the distance between the conformations $c_i$ and $c_j$, that is $\dCalC{c_i}{c_j}$. 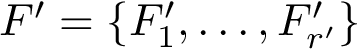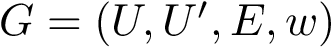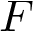Denoting $E$ the edge set of the MST, and $e={ c_i, c_j}$ a particular edge, we then report the following statistical summary for $G$:

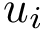
$ \min_{e\in E} \dCalC{c_i}{c_j}, \underset{e\in E} \median \dCalC{c_i}{c_j}, \max_{e\in E} \dCalC{c_i}{c_j}. $

To intuitively capture the significance of this summary, consider the situation where the ensemble has a cluster structure, with dense regions separated by mostly empty space. In that case, most of the edges are short ones, only those connecting clusters being long ones, which reads plainly from the statistical summary.

Persistence based clustering

When an ensemble features clusters, as e.g. seen from the statistical summary from the edge lengths found in a MST, the next step consists of finding these clusters. Upon estimating the sample density at each sample from the ensemble, a three stage strategy consists of associating one cluster to each local maximum of the estimated density [53] , [93], and to filter out spurious (i.e. small) ones. We now briefly review these steps.

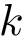
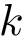
The first task is the density estimation. Assume that a nearest neighbors graph (NNG) has been built, so that each sample is linked to a number of its nearest neighbors, say its $k$ nearest neighbors. Intuitively, the density about a sample is inversely proportional to the distances to the nearest neighbors. 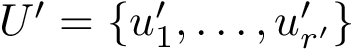Formally, denoting $k$ the number of nearest neighbors and $V_d$ the volume of the unit ball in $\mathbb{R}^d$, the local density at sample $c_i$ can be estimated as [22] :

$ \hat{f_n}(c) = \frac{1}{n\ V_d} \biggl(\frac{\sum_{j=1}^{k_n} j^{2/d}}{\sum_{j=1}^{k_n}(\dCalC{c}{n^j(c)})^2}\biggr)^{d/2} $

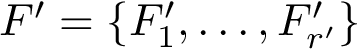
To define clusters, consider the lifted NNG obtained by endowing each sample with the previous estimated density. We define a cluster as the catchment basin (watershed) associated with a local maximum of the estimated density [52] . Along the way, spurious local maxima are filtered out using topological persistence [52] .
Prosaically, this process is analogous to that used in topography to define a peak on a mountain range: a peak $p$ is persistent if the elevation drop to the saddle leading to a higher peak, say $q$, is at least some user defined value. If not, the peak $p$ may be considered as a secondary peak of $q$. The user is referred to the package Morse_theory_based_analyzer for further details.

Due to the high dimensionality of configuration spaces of molecular systems, the estimate of Eq. (eq-estimated-density) is typically small. For such cases, persistence diagrams used to perform the simplification (see again the package Morse_theory_based_analyzer ) are best plotted in log-log scale.


Computing pairwise distances

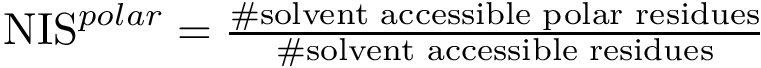
Computing pairwise distances between (selected) conformations, so as e.g. to run a dimensionality reduction algorithm such as multi-dimensional scaling or Isomap. Such low dimensional embeddings are indeed highly convenient to visualize the relative position of a set of conformations, e.g. low lying local minima.

To this end, we proceed in two steps:

  • First, all conformations are aligned in the same coordinate system, as specified by Eq. eq-aligned-conformations.

  • Second, pairwise Euclidean distances are computed between these conformations. The resulting distance matrix is then easily converted into a Gram matrix, from which multi-dimensional scaling can be executed [116].

Input: Specifications and File Types

The input is a list of conformations of the same molecule, and can be provided with several format:

  • PDB files: the input is a file listing PDB files of the same molecule
  • Conformation file: the input is a file listing each conformation as a D-dimensional point, i.e the dimension of the conformation followed by the (x, y, z) coordinates of all the atoms, just separated by a blank 
    6 x11 y11 z11 x12 y12 z12
6 x21 y21 z21 x22 y22 z22
6 x31 y31 z31 x32 y32 z32
...
  • Gromacs xtc file: the input is a file generated by the Gromacs software

It is also possible to provide an XML archive containing a boost graph representing the precomputed nearest neighbours graph (in order to skip the sometimes time consuming construction of the nng). All analysis are optional, so that they have to be specified in the command-line. For example, running analysis over the sampling diversity is done using the option –sampling-diversity. Note that all other analysis require the computation of the nng, meaning that the option –nng-builder should be used. Thus, a calculation is launched as follows:

> sbl-conf-ensemble-analysis-lrmsd.exe --points-file data/bln69_sampling.txt --sampling-diversity --pairwise-distances --nng-builder --num-neighbors 10 --mst --mtb --directory results --verbose --output-prefix --log
The main options of the program $\sblCEAL$ are:
–points-file string: plain text file listing all conformations as D-dimensional points
–sampling-diversity: run Sampling Diversity Analysis
–nng-builder: run the NNG Builder
–num-neighbors int: Target number of neighbors for each vertex
–mst: run Minimal Spanning Tree Analysis
–mtb: run Morse Theory Based Analysis


File Name

Description

BLN69 conformations file

Sampling done from sbl-landexp-hybrid-BH-TRRT-BLN.exe

Input files for the run described in section Input: Specifications and File Types .

Output: Specifications and File Types

PreviewFile Name

Description

General: log file, sampling diversity and sampling sparsity

Log file

Log file containing high level information on the run of $\sblCEAL$

Analysis xml file

Global analysis serialized using Boost into an XML archive

Module pairwise distances

Distances plain text file

Matrix of pairwise distances

Module NNG builder

NNG xml file

NNG serialized using Boost into an XML archive

Module MTB analysis: persistence based clustering

Morse Smale Witten chain complex xml file

Morse Smale Witten chain complex serialized using Boost into an XML archive

Stable manifold partition xml file

XML archive listing the samples repartition by persistent basin

Disconnectivity forest image file

Disconnectivity forest drawn in eps file format

Sorted basins plain text file

List of all basins sorted by persistence

Persistence diagram plot script

Gnuplot script for the persistence diagram

Persistence diagram image

Persistence diagram drawn by gnuplot in pdf file format

Persistences plain text file

List of all finite persistences

Persistence histogram plot script

R script for the persistence histogram

Persistence histogram image

Persistence histogram drawn by R in pdf file format

Output files for the runs described in section Input: Specifications and File Types, classified by modules – see Fig. fig-cea-workflow .

Algorithms and Methods

Sampling diversity

Computing these measures requires performing a registration of each conformation into a unique coordinate system, as specified in Eq. (eq-aligned-conformations).

Using the first conformation $c_1$ as reference, one can transform every other conformation by applying to it the rigid transform defining the $\lrmsd$ between $c_i$ and $c_1$.

Sampling sparsity via spanning trees

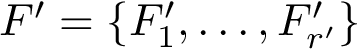
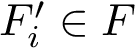
Extracting the MST out of a connected graph is a classical problem in computer science. We use Prim's algorithm, which iteratively attaches one node not connected yet, namely that using the shortest edge available which does not create a cycle.

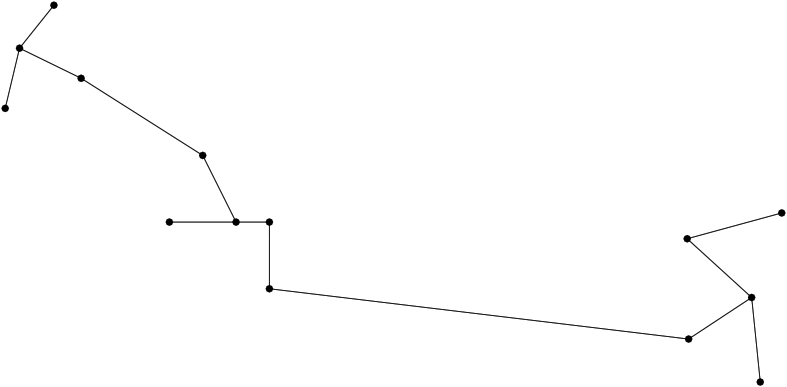A minimum spanning tree (MST) connecting conformations
The MST is computed once all conformations have been registered in the same coordinate system. The distribution of edge lengths provides information on the sampling density.

Persistence Based Clustering

Once the density has been estimated (Eq. eq-estimated-density), the persistence based clustering is carried out using the algorithms implemented in the package Morse_theory_based_analyzer. See also the module MTBA in the workflow of section Algorithms and Methods.

  • Changing the representation used for conformations.

  • Changing the distance between conformations.

In order to derive such versions, there are two important ingredients, that are the workflow class, and its traits class, as we shall see now.

The Traits Class

T_Conformational_ensemble_analysis_traits:

The Workflow Class

T_Conformational_ensemble_analysis_workflow: