 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: F. Cazals and J. Herrmann and E. Sarti
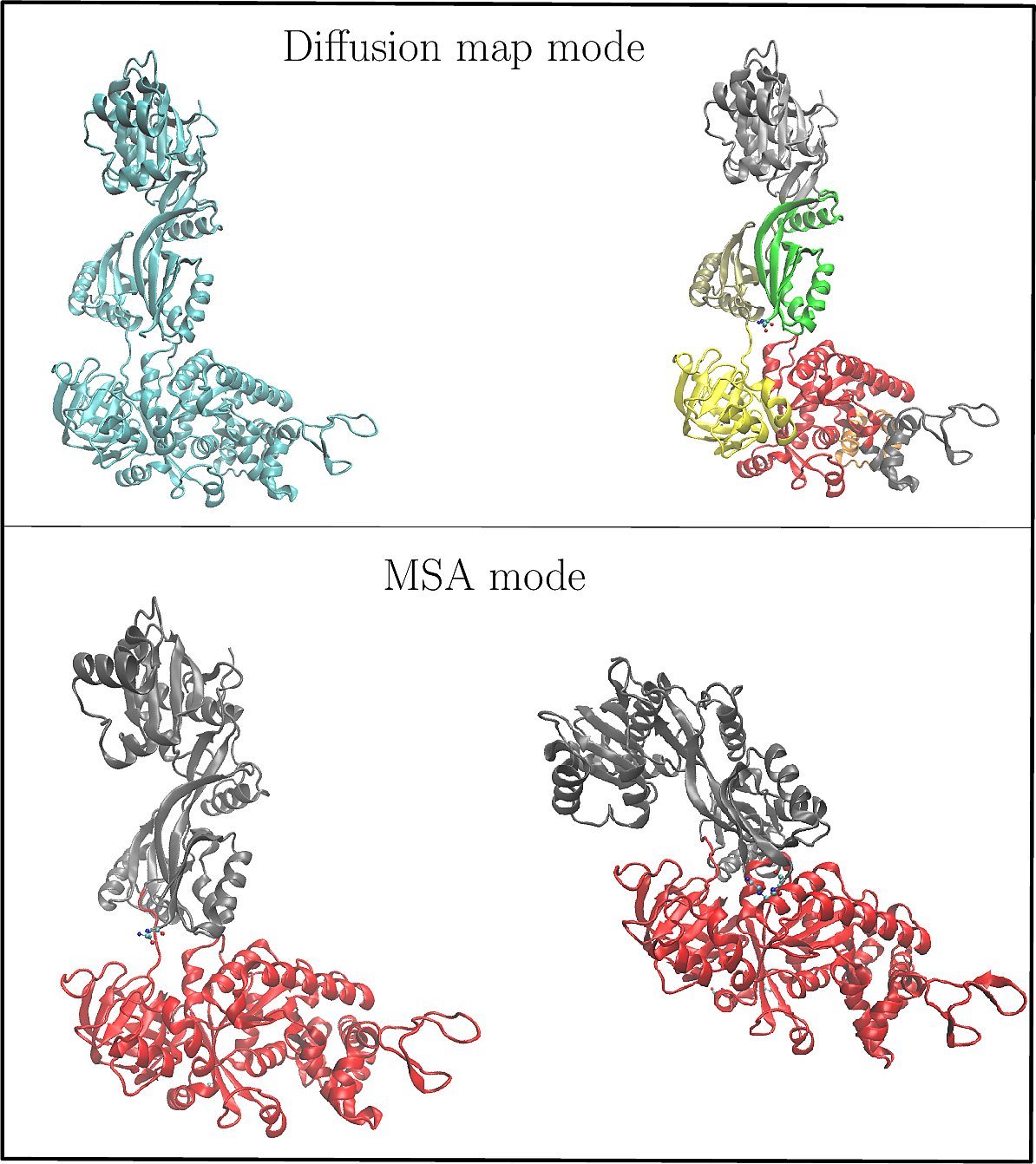
Defining domains within a polypeptide chain or protein amounts to maximizing intra-domain interactions while minimizing inter-domain interactions. This problem is closely related to graph partitioning techniques, and in particular spectral clustering [188].
The 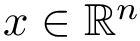
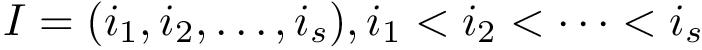
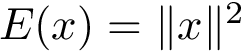
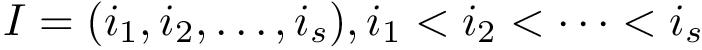
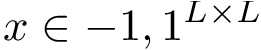
akin to the standard deviation of their mutual distance:
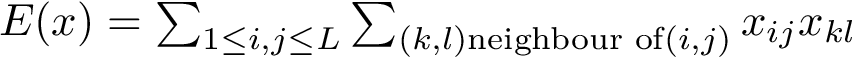
This fluctuation is turned into a similarity 


This package implements 
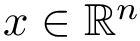
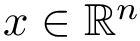
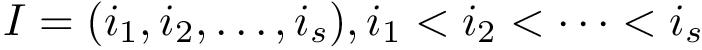
Background. We first provide some key elements.

Modes ENM and DM require a PDB/mmCIF file and the specification of a chain. These two modes use stiffness constants to encode pairwise contacts between residues. The default values are as follows:



Note that two amino acids may interact in different ways. For example, two a.a. on the same generatrix of a 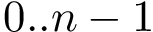





Mode MSA requires a multiple sequence alignment in FASTA format, as well as a file giving access to the structures processed. A position in the MSA is termed valid provided that no dash is present in that column, and all residues have been resolved in that structure. See below for details.
For a fixed value of 

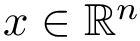




The main options of 
NB: run 
Output. We noted above that 





As illustrated in the notebook below, each line contains 5 numbers:
k,distance_stdev,ave_ratio_distances_NN1_NN2,norm_ave_ratio_distances_NN1_NN2,BIC




The SBL provides VMD, PyMOL, and Web plugins for sbl-spectraldom-run.py. Launch the VMD plugin from the SBL catalog under the Extensions menu, start the PyMOL plugin by running sbl_spectraldom in the PyMOL command line, and open the Web plugin from the SBL web plugins launcher page (served locally via sbl-web-plugins-launcher). All three plugins expose the same GUI and capabilities.
 |
| sbl-spectraldom plugin user interface. The user interface for the sbl-spectraldom plugin. The typical workflow is: Step 1: Set mode. Step 2: Provide input files (required files are different for different modes). Step 3: Set parameters for computation (leave it empty will use default value). Step 4: Choose an output directory (optional, a default is provided). Step 5: Launch the computation. Step 6: Inspect the results in the viewer. Step 7: Review the quality scores plot in the GUI. Step 8: (Optional) Use the update panel to view the results of different k values in the viewer. |
We now review the main steps of the algorithm, see [159] and [cazals2025simpler]. The user is also referred to Section Implementation for more details on the C++ classes involved.
We record contacts between pairs of residues, identified by their sequence numbers.



We now explain how the weights 
Mode Spectraldom_ENM. Following [13], an elastic network model (ENM) is built from covalent and non covalent contacts. The corresponding normal modes are computed, from which distance fluctuations for pairs of residues are obtained [13]. Denote 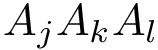



Mode Spectraldom_DM. As noted above, each pair of neighboring / interacting residues is assigned one or several stiffness values. In case of duplicate values for two residues, the max value is used – mode 
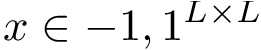


We take 
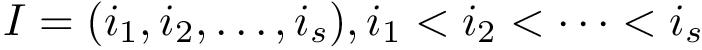

The corresponding matrix 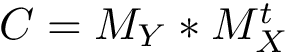
Mode Spectraldom_MSA. The multiple sequence alignment (MSA) mode handles the case of molecules with similar structures and disimilar sequences. Given a MSA, the atomic distance fluctuation of Eq. eq-fluct is computed from the distances observed in the structures.
The similarity matrix 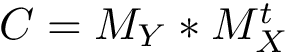
Consider the edge weighted undirected graph whose vertices are the individual residues, and whose edge weights are the 
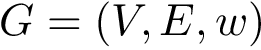
Consider the usual unnormalized Laplacian 


Then, one clusters the normalized rows of the 



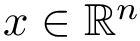




Fixed value of k. For a fixed value of 
Assume there are 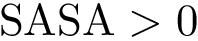
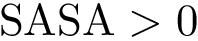


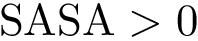


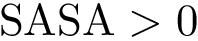

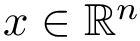


Repeats. For a fixed value of k, we perform 
Range for k and repeats. Consider now a range of values for ![$k \in [\kmin, \kmax]$](form_1340.png)
![$k \in [\kmin, \kmax]$](form_1340.png)


Quality plot. The quality plot is the box plot of the score Eq. eq-spectrusscore.

The following comments are in order regarding all parameters used:

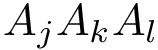
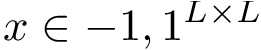

The implementation requires a diverse set of pieces, which we now briefly present.
Filters for residues in structures. The class SBL::CSB::T_Chains_residues_contiguous_indexer is used to record the residues present in the structures associated with the sequences of the MSA. Contiguous indices for resids are the contiguous integers which reference the resids, irrespective of gaps.
Multiple sequence alignments. Consider a MSA of length 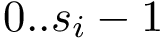
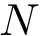
In order for atomic fluctuations to be computed using the same number of pairs (i.e. the binomial coefficient 
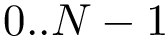
The class SBL::CSB::T_Multiple_sequence_alignment_DS is the data structure to handle MSA; it provides in particular the following two mappings:
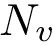
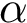
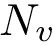

The previous class overlooks the presence of residues in the structures associated to the sequences of the MSI.
The class SBL::CSB::T_Multiple_sequence_alignment_DS_filtered has the same interface as SBL::CSB::T_Multiple_sequence_alignment_DS, except that it implements an extra check based on residues associated with a MSA position:
In practice, this latter check is provided by the class SBL::CSB::T_Chains_residues_contiguous_indexer. (Recall that this class contains a map from a residue sequence number (minus 1) to contiguous indices.)
Representation of polypeptide chains. The class SBL::CSB::T_Polypeptide_chain_representation from the package Protein_representation is used to access all pieces of information on polypeptide chains (covalent neighbors, atomic coordinates).
Contacts. Given a polypeptide chain, consider the following classes of contacts, defined as interacting residues
The class SBL::CSB::T_Polypeptide_chain_contacts_finder finds all such contacts, and provides them as pairs of residue sequence numbers –in (min, max) order. The search of non covalent contacts uses the spatial search engine from CGAL, based on Kd trees.
Instantiating this class uses the local class SBL::CSB::T_Point_xyz_with_atom , which contains the point used for spatial search (CGAL), and also knows the atom from the polypeptide chain representation.
Elatic Network Model and pairwise interactions. Given one polypeptide chain, the class SBL::CSB::T_Elastic_network_model implements the ENM model from [13] , providing in particular a calculation of anisotropic fluctuations associated with normal modes.
As usual, the structure processed may have missing residues at the C-ter and/or N-ter, and also within the structure. Also, its residue sequence numbers may start with negative values. On the other hand, indices in Eigen start at 0. Therefore, residue sequence numbers are converted to contiguous indices using the class SBL::CSB::T_Chains_residues_contiguous_indexer.
An ENM model can be seen as a graph whose vertices are residues, connected by edges.
The 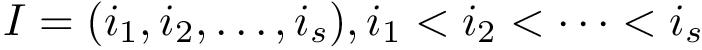
Contacts are sought between residue identified by their sequence numbers. These contacts are also converted to contiguous indices which can be used in Eigen matrices – Eigen indices start at 0.
Linear algebra operations are carried out using the Eigen library.
Clustering and spectral clustering. Spectral clustering is implemented in the class SBL::GT::T_Spectral_clustering, which is parameterized by a traits class provide an edge weighted boost graph. The weight 
The class SBL::GT::T_Spectral_clustering internally uses the generic version of 

Prefactors for kmeans. Prefactors are used in Eq. eq-spectrusscore . They are simply computed by running 


Spectraldom. We finally arrive at the class T_Spectraldom which implements the aforementioned three modes. Given that the DM and ENM modes use a single structure but not MSA, we use the following design pattern to handle the three modes coherently and comply with Defs. def-valid-msa-none and def-valid-msa-struct-none :
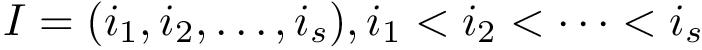
The Spectraldom traits class requires two types:
Back to structures from clusters. Let 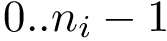
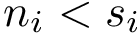
Main executable: 

Main script: sbl-spectraldom-run.py: a script calling 
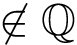
Reducing fragmentation: sbl-spectraldom-defrag.py: a script used to remove fragmentation of the domains identified. See paper [cazals2025simpler] for details.
Handling prefactors. To compute and manipulate prefactors involved in the scores 


Using these, proceed as follows:
// 1. Generate prefactors.csv sbl-spectraldom-generate-prefactor.exe --min_k 2 --max_k 20 // 2. Generate kmeans-prefactors.hpp, which contains a lookup table scripts/sbl-spectraldom-prefactor-header-writer.py -f build/prefactors.csv // 3. Compile again sbl-spectraldom.exe

See the following jupyter demos:
This notebook shows how to lauch the commands and comments on the outpout. It shows the quality plot obtained, but does not perform an interactive visualization of the structures -- which should be done with VMD or pymol. To run the notebook, a number of executables / scripts from the SBL must be available from one's PATH:
To find domains:
To perform flexible alignments
To compare the domains obtained against structural similarities identified by the flexible aligner Kpax:
To reduce the fragmentation of domains using the D-family-matching algorithm
import os, subprocess
from SBL_pytools import SBL_pytools
py = subprocess.run("which python3", shell=True, stdout=subprocess.PIPE).stdout.decode('utf-8').strip()
spectraldom_run_exe = subprocess.run("which sbl-spectraldom-run.py", shell=True, stdout=subprocess.PIPE).stdout.decode('utf-8').strip()
# We use sbl-spectraldom-run.py to run sbl-spectraldom.exe on chain A of 1ggg.pdb
# NB: the script dumps the command invoking sbl-spectraldom.exe
cmd = "%s %s --pdb-fpath data/DB-molecular-motions/1wdn.pdb --load-chains A --output-dir 1ggg-1wdn" % (py, spectraldom_run_exe)
#cmd = "sbl-spectraldom-run.py --pdb-fpath data/DB-molecular-motions/1wdn.pdb --load-chains A --output-dir 1ggg-1wdn"
print(cmd)
os.system(cmd)
ofile = SBL_pytools.find_file_in_output_directory("quality-score-plot.pdf", "1ggg-1wdn")
print("Quality plot file:", ofile)
SBL_pytools.show_pdf_file(ofile, 200)
/usr/bin/python3 /user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom-run.py --pdb-fpath data/DB-molecular-motions/1wdn.pdb --load-chains A --output-dir 1ggg-1wdn Pdb files found : Collected data/DB-molecular-motions/1wdn.pdb A +++ Running spectraldom in mode Spectraldom_DM Spectraldom mode DM/ENM: valid length and num residues are 223 223 residues ->Polypeptide_chain_contacts_finder... ...covalent_contacts num contacts 445 ...non_covalent_contacts contacts with distance threshold 10.00 is 4148 ->ENM::convert_contact_maps_to_triplets_ijstiff... ...stiffness CT_COV=10.00 : processing 445 contacts ...stiffness CT_NCOV=1.00 : processing 4148 contacts ...ENM check: num Calphas is 223 ...ENM::fill_DM_weights_matrix_from_residue_contacts in stiffness mode Stiffness_mode_max, matrix size 223 x 223 End compute_graph with 223 vertices and 4148 edges Spectral_clustering::compute_least_k_eigenvals ...Spectraldom: running k_means for k = 2 3 4 5 6 7 8 9 10 ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-best.csv ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-repeats.csv ---Spectraldom done ---Spectraldom done
/usr/local/lib64/python3.11/site-packages/Bio/PDB/StructureBuilder.py:89: PDBConstructionWarning: WARNING: Chain A is discontinuous at line 2187. warnings.warn(
['/user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom.exe', '--kmin', '2', '--kmax', '10', '--dmax-contacts', '10', '--mode', 'DM', '--filename', 'data/DB-molecular-motions/1wdn.pdb', '--load-chains', 'A', '--stiffness-cov', '10', '--stiffness-ncov', '1', '--dzero', '4.5', '--output-dir', '1ggg-1wdn']
/user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom.exe --kmin 2 --kmax 10 --dmax-contacts 10 --mode DM --filename data/DB-molecular-motions/1wdn.pdb --load-chains A --stiffness-cov 10 --stiffness-ncov 1 --dzero 4.5 --output-dir 1ggg-1wdn
#i################################################################################
+++ Spectraldom-run.py analysis...
#i################################################################################
K values for local maxima: [2, 5, 8]
Best clusterings are: ['1ggg-1wdn/spectraldom-clustering-1ggg-A-k2.txt', '1ggg-1wdn/spectraldom-clustering-1ggg-A-k5.txt', '1ggg-1wdn/spectraldom-clustering-1ggg-A-k8.txt']
=== Quality plot dumped:
okular 1ggg-1wdn/1ggg-1wdn-quality-score-plot.pdf
pdb-list here: [('data/DB-molecular-motions/1wdn.pdb', '1wdn', 'A')]
data/DB-molecular-motions/1wdn.pdb
pdbid:data/DB-molecular-motions/1wdn.pdb model idx:0 chain_id:A aa_in_primary_seq:226 aa_in_struct:223 resid_min:4 resid_max:226 resid_span:223
226 ; ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k10.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k2.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k2.spec
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k3.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k4.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k5.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k5.spec
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k6.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k7.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k8.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k8.spec
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k9.txt
=== (vmd) Commands for local maxima--in order of decreasing score:
vmd -e 1ggg-1wdn/vmd-1wdn-A-k2.vmd
vmd -e 1ggg-1wdn/vmd-1wdn-A-k5.vmd
vmd -e 1ggg-1wdn/vmd-1wdn-A-k8.vmd
--- Spectraldom-run.py analysis done
=== (rmsdcomb) Command to run the combined RMSD calculation:
sbl-rmsd-flexible-proteins-kpax.exe -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k2.spec --load-chains A -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k5.spec --load-chains A -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k8.spec --load-chains A
=== (dfam) Command to run DFAM on pairs of consecutive local maxima
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k10.txt -f 1ggg-1wdn/dfam-1wdn-A-k2.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k2.txt -f 1ggg-1wdn/dfam-1wdn-A-k3.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k3.txt -f 1ggg-1wdn/dfam-1wdn-A-k4.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k4.txt -f 1ggg-1wdn/dfam-1wdn-A-k5.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k5.txt -f 1ggg-1wdn/dfam-1wdn-A-k6.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k6.txt -f 1ggg-1wdn/dfam-1wdn-A-k7.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k7.txt -f 1ggg-1wdn/dfam-1wdn-A-k8.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k8.txt -f 1ggg-1wdn/dfam-1wdn-A-k9.txt --diameter-constraint 2 --num-iterations 100
Quality plot file: 1ggg-1wdn/1ggg-1wdn-quality-score-plot.pdf
GPL Ghostscript 10.02.1 (2023-11-01)
Copyright (C) 2023 Artifex Software, Inc. All rights reserved.
This software is supplied under the GNU AGPLv3 and comes with NO WARRANTY:
see the file COPYING for details.
Processing pages 1 through 1.
Page 1
# Note that the previous python command executes the following -- parameters removed when default options are used
# We re-execute the command and display the scores obtained
cmd = "sbl-spectraldom.exe --mode DM --filename data/DB-molecular-motions/1wdn.pdb --load-chains A --output-dir 1ggg-1wdn"
os.system(cmd)
SBL_pytools.show_txt_file("scores-best.csv", "1ggg-1wdn")
Pdb files found : Collected data/DB-molecular-motions/1wdn.pdb A +++ Running spectraldom in mode Spectraldom_DM Spectraldom mode DM/ENM: valid length and num residues are 223 223 residues ->Polypeptide_chain_contacts_finder... ...covalent_contacts num contacts 445 ...non_covalent_contacts contacts with distance threshold 10.00 is 4148 ->ENM::convert_contact_maps_to_triplets_ijstiff... ...stiffness CT_COV=10.00 : processing 445 contacts ...stiffness CT_NCOV=1.00 : processing 4148 contacts ...ENM check: num Calphas is 223
...Total num of contacts irrespective of type is 4593
...ENM::fill_DM_weights_matrix_from_residue_contacts in stiffness mode Stiffness_mode_max, matrix size 223 x 223 End compute_graph with 223 vertices and 4148 edges Spectral_clustering::compute_least_k_eigenvals ...Spectraldom: running k_means for k = 2 3 4 5 6 7 8 9 10 ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-best.csv ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-repeats.csv ---Spectraldom done ---Spectraldom done ++Showing file 1ggg-1wdn/scores-best.csv k,distance_stdev,ave_ratio_distances_NN1_NN2,norm_ave_ratio_distances_NN1_NN2,BIC 2,0.193751,11.7061,3.64167,1771.54 3,0.290992,6.14169,3.11373,1767.03 4,0.428361,3.73126,2.26465,1627.85 5,0.404445,4.06242,2.71721,1802.58 6,0.426511,3.50872,2.47955,1884.71 7,0.44494,3.27514,2.39112,1955.24 8,0.44334,3.49367,2.60198,2082.8 9,0.474657,3.38504,2.56302,2073.6 10,0.468722,3.14924,2.41573,2218.93 --Done
# 1. Align chains A of and show the resulting FASTA file
pdb_align_exe = subprocess.run("which sbl-pdb-align.py", shell=True, stdout=subprocess.PIPE).stdout.decode('utf-8').strip()
cmd = "%s %s -f data/DB-molecular-motions/1ggg.pdb data/DB-molecular-motions/1wdn.pdb --chains A A --output-dir 1ggg-1wdn" % (py, pdb_align_exe)
print(cmd)
os.system(cmd)
SBL_pytools.show_txt_file( "1ggg-1wdn.fasta", "1ggg-1wdn")
# 2. Run spectraldom
cmd = f"{py} {spectraldom_run_exe} --msa-fpath 1ggg-1wdn/1ggg-1wdn.fasta --structures-fpath 1ggg-1wdn/1ggg-1wdn.txt --output-dir 1ggg-1wdn"
print(cmd)
os.system(cmd)
qplot = SBL_pytools.find_file_in_output_directory("quality-score-plot.pdf", "1ggg-1wdn")
print("Quality plot file:", qplot)
SBL_pytools.show_pdf_file(qplot, 200)
/usr/bin/python3 /user/fcazals/home/projects/proj-soft/sbl/scripts/sbl-pdb-align.py -f data/DB-molecular-motions/1ggg.pdb data/DB-molecular-motions/1wdn.pdb --chains A A --output-dir 1ggg-1wdn pdb_id1ggg.pdb and chain A: Sequence has length: 226 pdb_id1wdn.pdb and chain A: Sequence has length: 226 +++Seq align with Bio.pairwise2 num alignments with scores: 1 [1164.0] Dumped txt file 1ggg-1wdn/1ggg-1wdn.txt Dumped fasta file 1ggg-1wdn/1ggg-1wdn.fasta +++Struct align, num residues chain_1:220 chain_2:222 intersection:220 lRMSD for the id alignment using 220 residues: 5.34 Dumped file data/DB-molecular-motions/1wdn-aligned.pdb PDB files: data/DB-molecular-motions/1ggg.pdb data/DB-molecular-motions/1wdn-aligned.pdb vmd -e 1ggg-1wdn/1ggg-A--1ggg-A.vmd ++Showing file 1ggg-1wdn/1ggg-1wdn.fasta >data/DB-molecular-motions/1ggg.pdb_A ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK >data/DB-molecular-motions/1wdn.pdb_A ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK --Done /usr/bin/python3 /user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom-run.py --msa-fpath 1ggg-1wdn/1ggg-1wdn.fasta --structures-fpath 1ggg-1wdn/1ggg-1wdn.txt --output-dir 1ggg-1wdn Pdb files found : Collected data/DB-molecular-motions/1ggg.pdb A Collected data/DB-molecular-motions/1wdn.pdb A +++ Running spectraldom in mode Spectraldom_MSA Spectraldom mode MSA: valid length and alignment length are 220 226 residues Spectraldom::initialize_sparse_fluctuation_matrix upper triangular used/unused/total/n*n: 1281/22809/24090/48400 Distance threshold used for contacts dmax=10.00 MSA Calpha_dist upper triangular matrix of dim 220 and with with binom(n,2) = 1281 entries MSA fluctuations computed: 1281 pairs out of 220x220=48400 possible ones T_Spectraldom::compute_similarity_matrix_from_fluctuations_vai:: fluctuation mean/median are 0.48/0.25 End compute_graph with 220 vertices and 1281 edges Spectral_clustering::compute_least_k_eigenvals ...Spectraldom: running k_means for k = 2 3 4 5 6 7 8 9 10 ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-best.csv ...Spectraldom: dumping scores /home/fcazals/projects/proj-soft/sbl/Applications/Spectral_domain_explorer/demos/Spectral_domain_explorer/1ggg-1wdn/scores-repeats.csv ---Spectraldom done ---Spectraldom done
/usr/local/lib64/python3.11/site-packages/Bio/PDB/StructureBuilder.py:89: PDBConstructionWarning: WARNING: Chain A is discontinuous at line 3924. warnings.warn( /usr/local/lib64/python3.11/site-packages/Bio/PDB/StructureBuilder.py:89: PDBConstructionWarning: WARNING: Chain B is discontinuous at line 4004. warnings.warn( /usr/local/lib64/python3.11/site-packages/Bio/PDB/StructureBuilder.py:89: PDBConstructionWarning: WARNING: Chain A is discontinuous at line 2187. warnings.warn(
['/user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom.exe', '--kmin', '2', '--kmax', '10', '--dmax-contacts', '10', '--mode', 'MSA', '--msa-fpath', '1ggg-1wdn/1ggg-1wdn.fasta', '--structures-fpath', '1ggg-1wdn/1ggg-1wdn.txt', '--output-dir', '1ggg-1wdn']
/user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-spectraldom.exe --kmin 2 --kmax 10 --dmax-contacts 10 --mode MSA --msa-fpath 1ggg-1wdn/1ggg-1wdn.fasta --structures-fpath 1ggg-1wdn/1ggg-1wdn.txt --output-dir 1ggg-1wdn
#i################################################################################
+++ Spectraldom-run.py analysis...
#i################################################################################
K values for local maxima: [2, 5, 9]
Best clusterings are: ['1ggg-1wdn/spectraldom-clustering-1ggg-A-k2.txt', '1ggg-1wdn/spectraldom-clustering-1ggg-A-k5.txt', '1ggg-1wdn/spectraldom-clustering-1ggg-A-k9.txt']
=== Quality plot dumped:
okular 1ggg-1wdn/1ggg-1wdn-quality-score-plot.pdf
pdb-list here: [('data/DB-molecular-motions/1ggg.pdb', '1ggg', 'A'), ('data/DB-molecular-motions/1wdn.pdb', '1wdn', 'A')]
data/DB-molecular-motions/1ggg.pdb
pdbid:data/DB-molecular-motions/1ggg.pdb model idx:0 chain_id:A aa_in_primary_seq:226 aa_in_struct:220 resid_min:5 resid_max:224 resid_span:220
226 ; ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK
pdbid:data/DB-molecular-motions/1ggg.pdb model idx:0 chain_id:B aa_in_primary_seq:226 aa_in_struct:220 resid_min:5 resid_max:224 resid_span:220
226 ; ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k10.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k2.txt
Dumped 1ggg-1wdn/domains-1ggg-A-k2.spec
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k3.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k4.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k5.txt
Dumped 1ggg-1wdn/domains-1ggg-A-k5.spec
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k6.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k7.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k8.txt
(dfam) Dumped 1ggg-1wdn/dfam-1ggg-A-k9.txt
Dumped 1ggg-1wdn/domains-1ggg-A-k9.spec
=== (vmd) Commands for local maxima--in order of decreasing score:
vmd -e 1ggg-1wdn/vmd-1ggg-A-k2.vmd
vmd -e 1ggg-1wdn/vmd-1ggg-A-k5.vmd
vmd -e 1ggg-1wdn/vmd-1ggg-A-k9.vmd
data/DB-molecular-motions/1wdn.pdb
pdbid:data/DB-molecular-motions/1wdn.pdb model idx:0 chain_id:A aa_in_primary_seq:226 aa_in_struct:223 resid_min:4 resid_max:226 resid_span:223
226 ; ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k10.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k2.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k2.spec
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k3.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k4.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k5.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k5.spec
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k6.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k7.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k8.txt
(dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k9.txt
Dumped 1ggg-1wdn/domains-1wdn-A-k9.spec
=== (vmd) Commands for local maxima--in order of decreasing score:
vmd -e 1ggg-1wdn/vmd-1wdn-A-k2.vmd
vmd -e 1ggg-1wdn/vmd-1wdn-A-k5.vmd
vmd -e 1ggg-1wdn/vmd-1wdn-A-k9.vmd
--- Spectraldom-run.py analysis done
=== (rmsdcomb) Command to run the combined RMSD calculation:
sbl-rmsd-flexible-proteins-kpax.exe -f 1ggg.pdb --domain-labels 1ggg-1wdn/domains-1ggg-A-k2.spec --load-chains A -f 1ggg.pdb --domain-labels 1ggg-1wdn/domains-1ggg-A-k5.spec --load-chains A -f 1ggg.pdb --domain-labels 1ggg-1wdn/domains-1ggg-A-k9.spec --load-chains A -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k2.spec --load-chains A -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k5.spec --load-chains A -f 1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k9.spec --load-chains A
=== (dfam) Command to run DFAM on pairs of consecutive local maxima
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k10.txt -f 1ggg-1wdn/dfam-1wdn-A-k2.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k2.txt -f 1ggg-1wdn/dfam-1wdn-A-k3.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k3.txt -f 1ggg-1wdn/dfam-1wdn-A-k4.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k4.txt -f 1ggg-1wdn/dfam-1wdn-A-k5.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k5.txt -f 1ggg-1wdn/dfam-1wdn-A-k6.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k6.txt -f 1ggg-1wdn/dfam-1wdn-A-k7.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k7.txt -f 1ggg-1wdn/dfam-1wdn-A-k8.txt --diameter-constraint 2 --num-iterations 100
sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k8.txt -f 1ggg-1wdn/dfam-1wdn-A-k9.txt --diameter-constraint 2 --num-iterations 100
Quality plot file: 1ggg-1wdn/1ggg-1wdn-quality-score-plot.pdf
GPL Ghostscript 10.02.1 (2023-11-01)
Copyright (C) 2023 Artifex Software, Inc. All rights reserved.
This software is supplied under the GNU AGPLv3 and comes with NO WARRANTY:
see the file COPYING for details.
Processing pages 1 through 1.
Page 1
cmd = "sbl-kpax-iterative-alignment.exe -f data/DB-molecular-motions/1ggg.pdb -f data/DB-molecular-motions/1wdn.pdb --load-chains A --load-chains A -v 2"
os.system(cmd)
Running: sbl-kpax-iterative-alignment.exe -f data/DB-molecular-motions/1ggg.pdb -f data/DB-molecular-motions/1wdn.pdb --load-chains A --load-chains A -v 2 Protein representation loader Statistics: Number of loaded PDB files: 2 Details for each file: -- file 1 data/DB-molecular-motions/1ggg.pdb: -- -- File exists: Yes -- -- File is valid: Yes -- -- Number of models: 1 -- -- Number of loaded atoms (of model with lowest index): 1714 -- -- Number of loaded SS bonds: 0 -- -- Number of discarded atoms based on model id (all models): 0 -- -- Number of discarded atoms based on chain id (all models): 1793 -- -- Number of discarded atoms based on b factor beeing too high (all models): 0 -- -- Number of discarded waters (all models): 159 -- -- Number of discarded hetatoms (all models): 159 -- -- Number of discarded hydrogens (all models): 0 -- -- Number of discarded alternate location atoms (all models): 0 -- -- Number of actually discarded atoms (all models): 1873 -- file 2 data/DB-molecular-motions/1wdn.pdb: -- -- File exists: Yes -- -- File is valid: Yes -- -- Number of models: 1 -- -- Number of loaded atoms (of model with lowest index): 1740 -- -- Number of loaded SS bonds: 0 -- -- Number of discarded atoms based on model id (all models): 0 -- -- Number of discarded atoms based on chain id (all models): 9 -- -- Number of discarded atoms based on b factor beeing too high (all models): 0 -- -- Number of discarded waters (all models): 122 -- -- Number of discarded hetatoms (all models): 122 -- -- Number of discarded hydrogens (all models): 0 -- -- Number of discarded alternate location atoms (all models): 0 -- -- Number of actually discarded atoms (all models): 131 Covalent Structure File Loader statistics: -- -- Number of molecular covalent structures: 2 -- Molecular covalent structure 0: -- -- Number of particles: 7150 -- -- Number of embedded particles: 1714 -- -- Number of bonds: 7212 -- -- Number of embedded bonds: 1744 -- -- Number of disulfide bonds: 0 -- Molecular covalent structure 1: -- -- Number of particles: 3593 -- -- Number of embedded particles: 1740 -- -- Number of bonds: 3623 -- -- Number of embedded bonds: 1771 -- -- Number of disulfide bonds: 0 Protein Representation Loader statistics: Number of loaded proteins: 2 Details for each protein : -- structure 1: -- -- Number of chains: 1 -- -- Number of residues: 220 -- -- Number of particles: 3575 -- -- Number of embedded particles: 1714 -- -- Number of bonds: 3606 -- -- Number of embedded bonds: 1744 -- structure 2: -- -- Number of chains: 1 -- -- Number of residues: 223 -- -- Number of particles: 3575 -- -- Number of embedded particles: 1740 -- -- Number of bonds: 3606 -- -- Number of embedded bonds: 1771 Iterative alignment Starting module SBL::Modules::T_Alignment_structures_module...
Seeder_DP_score:alignment size:221
Statistics: Alignment length: 164 Alignment score : 74.435674 Alignment identity percentage: 0.378049 Alignment similarity percentage: 0.445122 Alignment lRMSD : 3.275461 Alignment dRMSD : 2.395408 Report... Ending module SBL::Modules::T_Alignment_structures_module... End Run General Statistics: Times elapsed for computations (in seconds): -- Iterative alignment: 2.172181 Total: 2.172181
0
cmd="sbl-rmsd-flexible-proteins-kpax.exe -f data/DB-molecular-motions/1ggg.pdb --domain-labels 1ggg-1wdn/domains-1ggg-A-k2.spec --load-chains A -f data/DB-molecular-motions/1wdn.pdb --domain-labels 1ggg-1wdn/domains-1wdn-A-k2.spec --load-chains A --directory-output 1ggg-1wdn"
os.system(cmd)
SBL_pytools.show_txt_file("rmsd-flexible-proteins-kpax__labels_lrmsd.txt", "1ggg-1wdn")
++Showing file 1ggg-1wdn/sbl-rmsd-flexible-proteins-kpax__labels_lrmsd.txt Label comparison between chain A of and chain A of -- one line: label lRMSD #amino acids Dom-0 3.809 124 Dom-1 4.062 96 Weighted lRMSD 3.921 involving a total of 220 amino acids --Done
defrag_exe = subprocess.run("which sbl-spectraldom-defrag.py", shell=True, stdout=subprocess.PIPE).stdout.decode('utf-8').strip()
cmd = f"%s %s -r 1ggg-1wdn -s data/DB-molecular-motions/1wdn.pdb -c A" % (py, defrag_exe)
os.system(cmd)
Peaks: [2, 5] sbl-cmp-clust-dfam.exe -f 1ggg-1wdn/dfam-1wdn-A-k2.txt -f 1ggg-1wdn/dfam-1wdn-A-k5.txt --diameter-constraint 2 --num-iterations 100 WARNING: VoI modified !! Now it's normalized by 2log(K) Postprocessing_Metaclusters_VoI -0.0 data/DB-molecular-motions/1wdn.pdb pdbid:data/DB-molecular-motions/1wdn.pdb model idx:0 chain_id:A aa_in_primary_seq:226 aa_in_struct:223 resid_min:4 resid_max:226 resid_span:223 226 ; ADKKLVVATDTAFVPFEFKQGDLYVGFDVDLWAAIAKELKLDYELKPMDFSGIIPALQTKNVDLALAGITITDERKKAIDFSDGYYKSGLLVMVKANNNDVKSVKDLDGKVVAVKSGTGSVDYAKANIKTKDLRQFPNIDNAYMELGTNRADAVLHDTPNILYFIKTAGNGQFKAVGDSLEAQQYGIAFPKGSDELRDKVNGALKTLRENGTYNEIYKKWFGTEPK (dfam) Dumped 1ggg-1wdn/dfam-1wdn-A-k0.txt === (vmd) Commands for local maxima--in order of decreasing score:
/usr/local/lib64/python3.11/site-packages/Bio/PDB/StructureBuilder.py:89: PDBConstructionWarning: WARNING: Chain A is discontinuous at line 2187. warnings.warn(
0