 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: F. Cazals and T. Dreyfus and C. Robert and A. Roth

In this package, we consider the problem of sampling a landscape, that is a height function defined as the real valued multivariate function. In biophysics, we notice, though, that this function typically codes the potential energy of a molecular system, so that the landscape is the potential energy landscape (PEL).
The algorithms presented fall in the realm of Monte Carlo based methods, in a broad sense. The precise meaning of sampling shall depend on the specific algorithms presented, as one may want in particular to:
Locate the low lying local minima of the function, with potentially a focus on the global minimum.
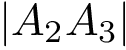
We actually provide a generic framework to develop such algorithms, providing instantiations for classical algorithms as well as algorithms developed recently.
Of particular interest in the sequel are the following three algorithms:
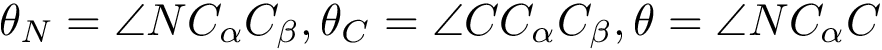
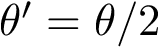
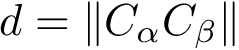
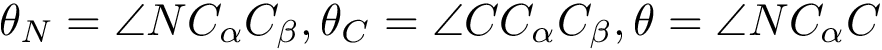
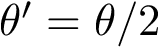
Practically, our main focus is on landscapes encoding the potential energy of a molecular system. Yet, our algorithms also handle the case of a multivariate real-valued function void of biophysical meaning. The ability to handle such diverse cases owes to a generic framework. We illustrate it by providing explorer in three settings:
For a protein model known as BLN69, defined over a configuration space of dimension 3x69=207, see section BLN69,
For small peptides such as pentalanine using the Amber force field, defined over a configuration space of variable dimension (3x53=159 for pentalanine),
Needless to stress that these are simple examples, and that instantiations of our exploration algorithms are easily derived by instantiating our generic classes.
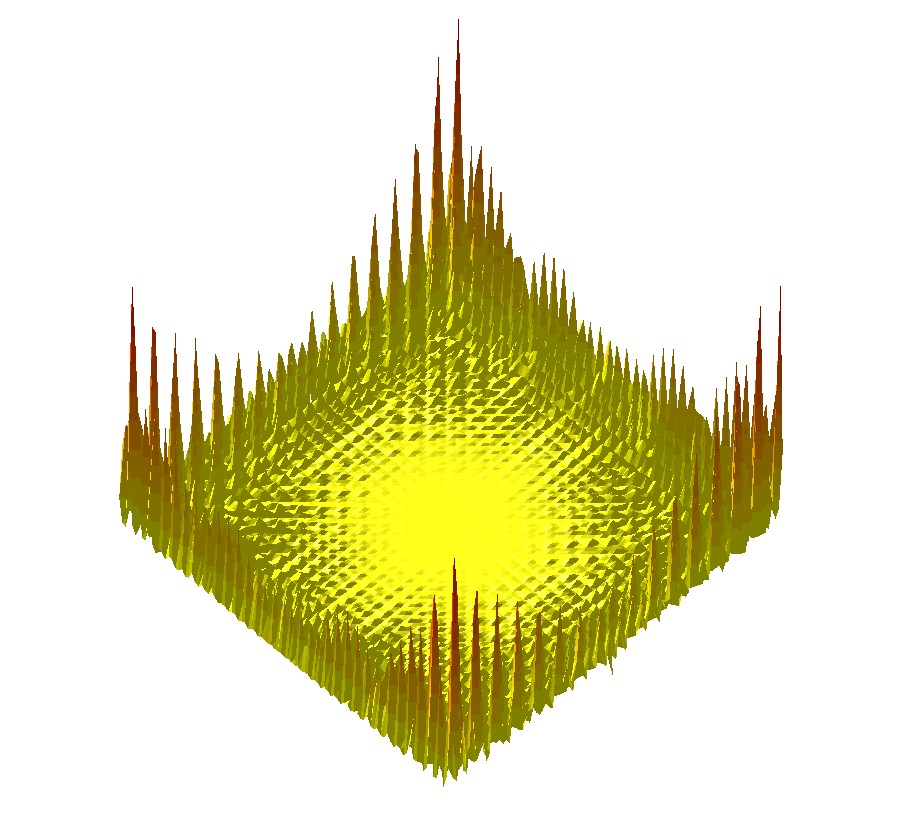 | ||
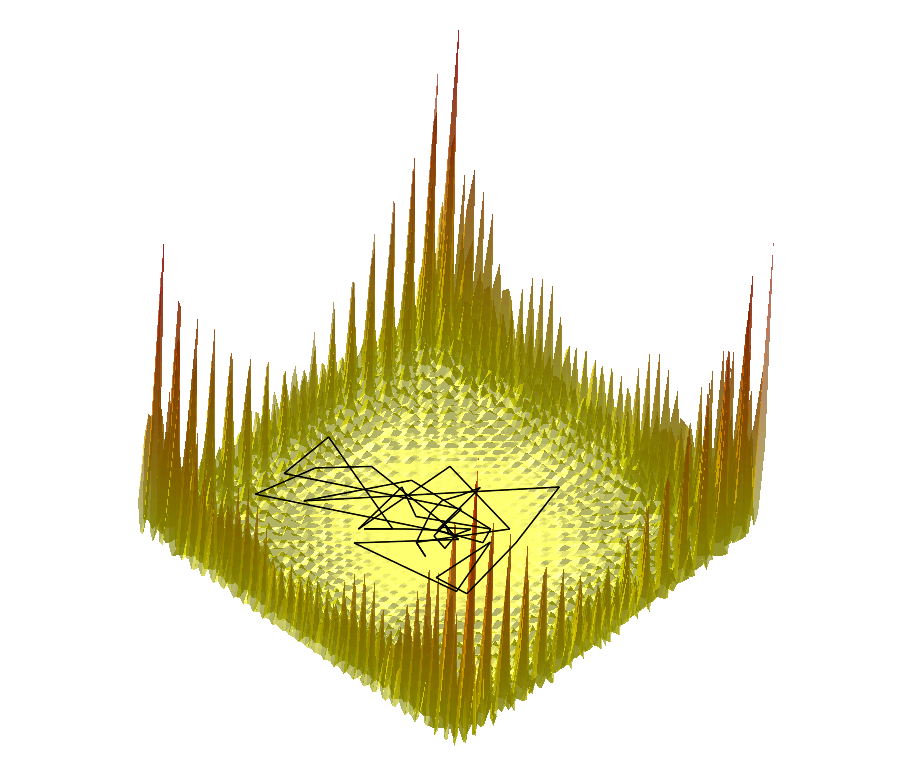 | 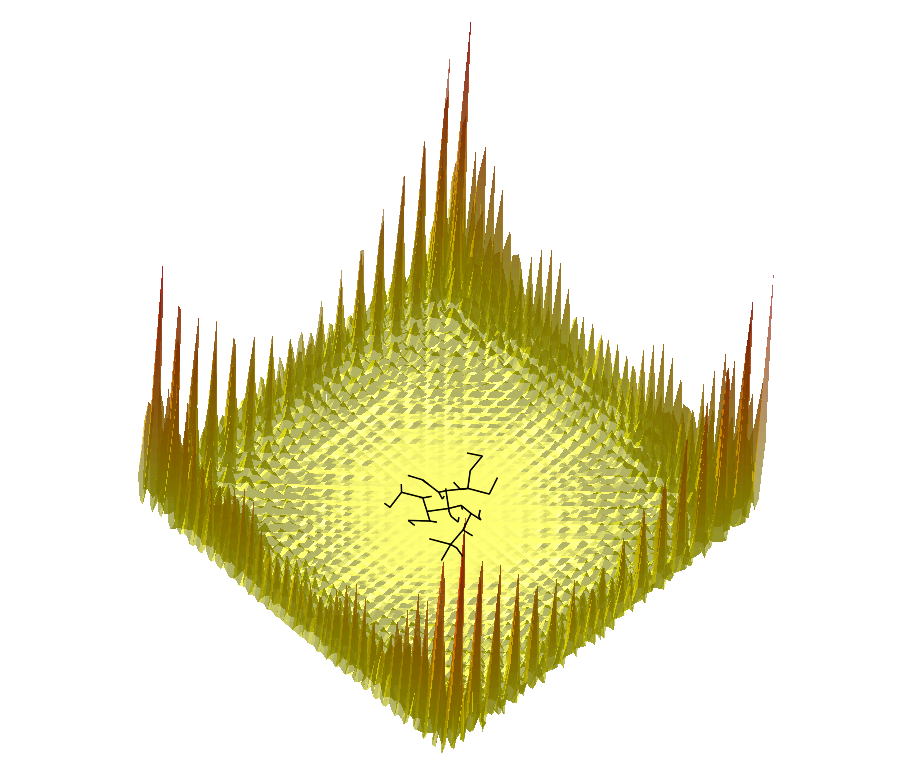 | 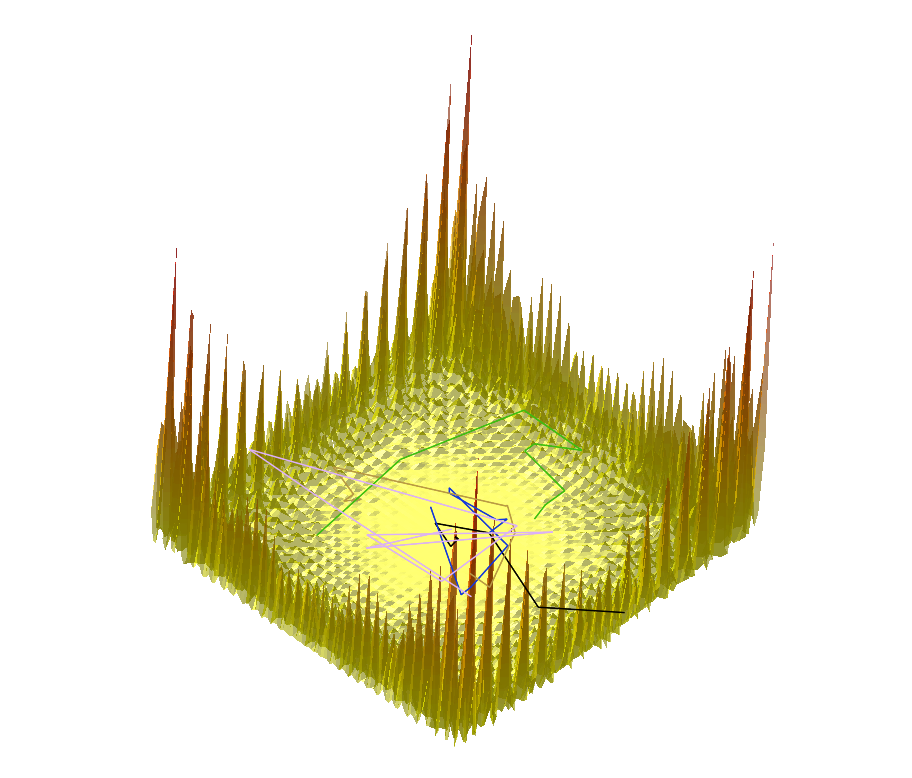 |
Comparing the explorations on the trigonometric terrain Top.Trigonometric terrain to be explored : Bottom. From Left to Right : Basins Hopping, TRRT and Hybrid. 50 minima (samples for TRRT) were generated. For TRRT, the initial displace delta was 0.5, while for Basins Hopping and Hybrid, it was 0.0001. For the Hybrid algorithm, Basins Hopping is used 10 times, then TRRT is used once : the consecutive minima generated by Basins Hopping are linked with rays of the same color. | ||
We first introduce a generic algorithm, thanks to which we shall instantiate all our algorithms.
Generic algorithm. A generic template (Algorithm alg-landexp-generic) describes the three aforementioned algorithms, and a number of variants. In addition to a stop condition (stating e.g. whether the number of conformations desired has been reached), this template consists of six main steps, namely:
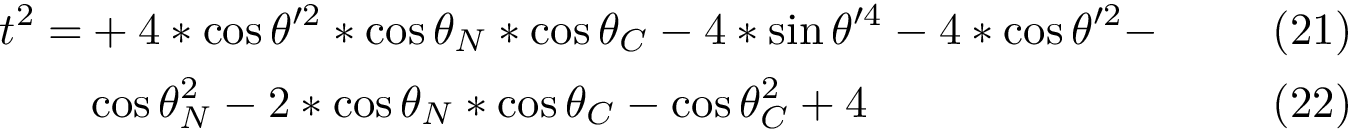
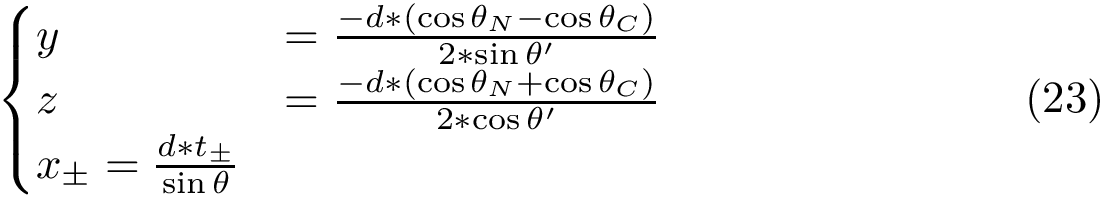
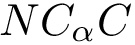
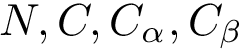
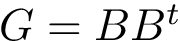

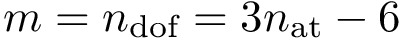
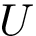
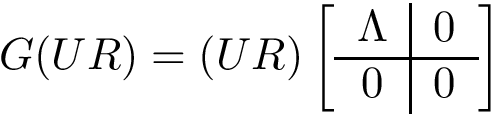
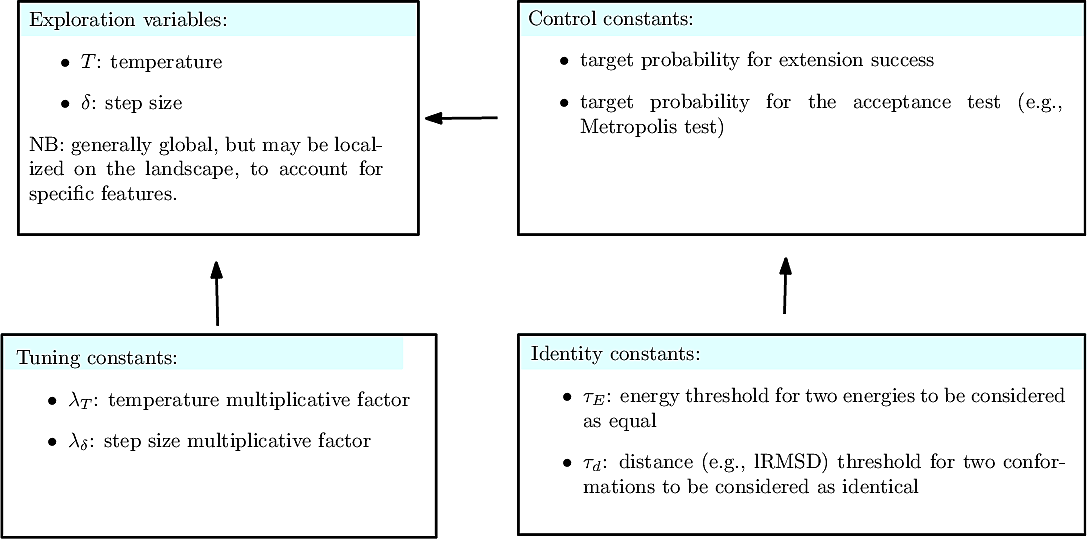
Parameters of the algorithm. By parameters of an algorithm, we refer to the variables and constants which shape its behavior. We distinguish four types of parameters (Fig. fig-landexp-explo-params):
Exploration variables: the core variables governing the exploration. The typical such variables are the temperature 
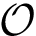
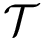
Tuning constants: multiplicative values used to evolve the exploration variables.
Control constants: the constants controlling how exploration variables are evolved. The typical constants are:
Exploration variables: target probability for the success of an extension.
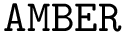
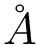
 |
| Exploration parameters Parameters i.e. variables and constants used by the algorithms. |
Details for 
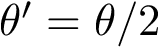
Details for 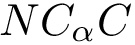
To perform an extension, see function 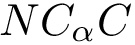
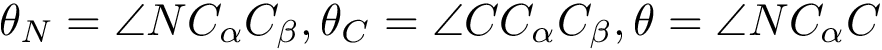
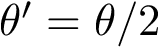
Because the extension is in general an expensive operations, an adaptation mechanism for the parameters governing the move set is called for, whence the function 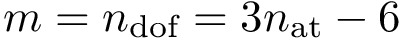
Details for 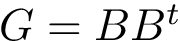
Details for 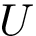
Yet, several default tuning modes are offered:
the default method consists on decreasing the temperature each time a sample is accepted, and increasing the temperature after a number of consecutive failures.
the probability method attempts to reach a given target acceptance ratio for the acceptance test. In this mode, every 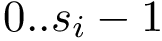
Details for 
In recording conformations, we face two cases which are detailed below:
Without filtering data structure: the case of 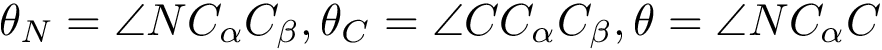
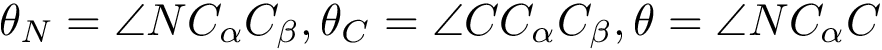
rm -f $1_uniq.txt; touch $1_uniq.txt;
rm -f $1_energies_uniq.txt; touch $1_energies_uniq.txt;
zero=0
i=1
while read p; do
count=$(grep -c "$p" "$1_uniq.txt")
if [ "$count" -eq "$zero" ]; then
echo "$p" >> "$1_uniq.txt"
sed "${i}q;d" "$1_energies.txt" >> "$1_energies_uniq.txt"
fi
((i++))
done < $1.txt
Indeed, this does not guarantee anymore the number of different minima / samples that have been visited.
With filtering data structure: the case of 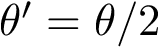
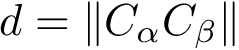
As mentioned above, filtering consists in identifying duplicates, at a sub-linear cost with respect to the conformations already identified. We distinguish filtering on the energy and on distances.
Filtering on energy commonly consists of checking that the energy of a newly found conformation differs by an amount 
Filtering on energies is in general not sufficient though, since the set, in conformational space, of conformations having a prescribed energy is generically a 
To filter on distances (e.g., using the least root-mean-square deviation, 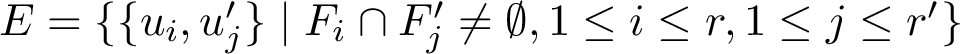
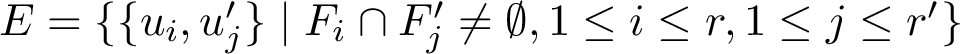
Details for 
the number of samples criterion : the algorithm stops when a number of registered conformations is reached.
the landmarks criterion: the algorithm stops once given specified landmarks have been visited—up to a distance criterion.
the quenched to landmarks criterion: each sample is quenched, and the algorithm halts when the local minima specified have been visited—up to a distance criterion.
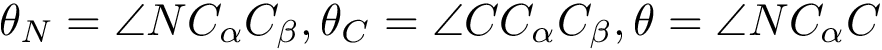
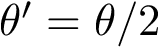
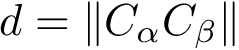
Instantiation for 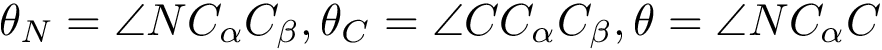
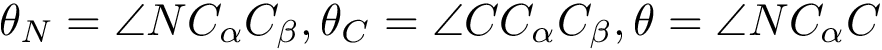
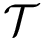
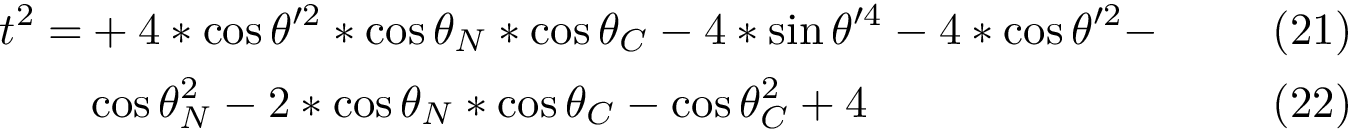
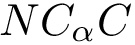
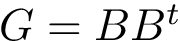

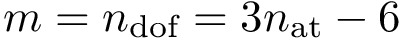
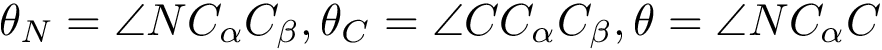
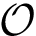
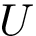
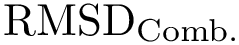
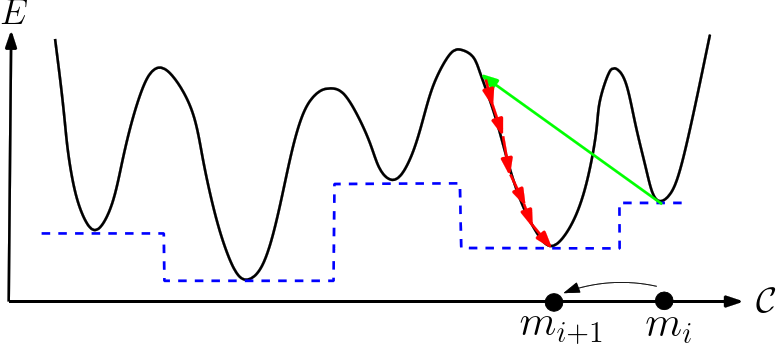 |
| The basin hopping algorithm The algorithm performs a walk in the space of local minima. Upon generating a new conformation by applying a move set to a local minimum |
BH may be used to explore any model (mathematical function, toy protein model BLN, regular atomic model, etc). Since every such model yields a different executable, this executable is referred to as sbl-landexp-BH-NAME-OF-MODEL.exe in the sequel.
The Jupyter notebook provided in this user manual uses several such executables.
Main options.
Input.
Main output.
Optional output.
Comments.
Instantiation for 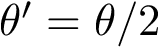
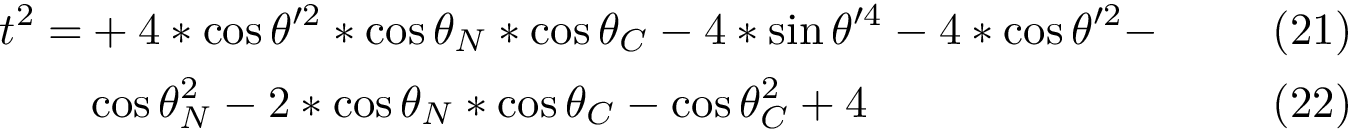
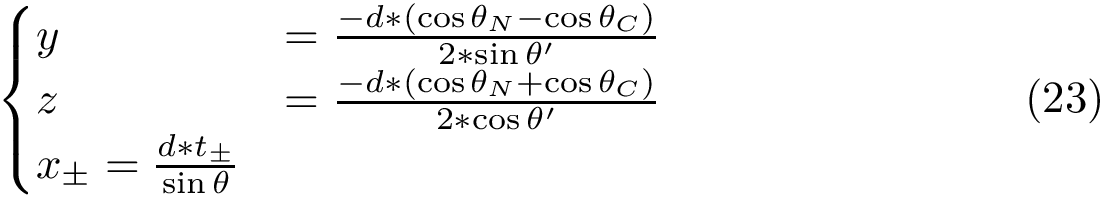
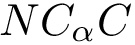
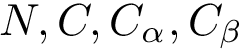
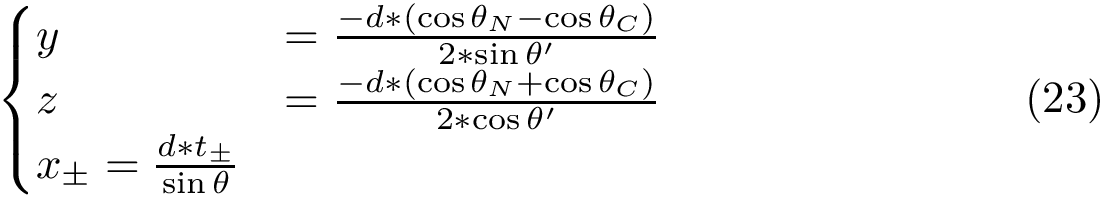
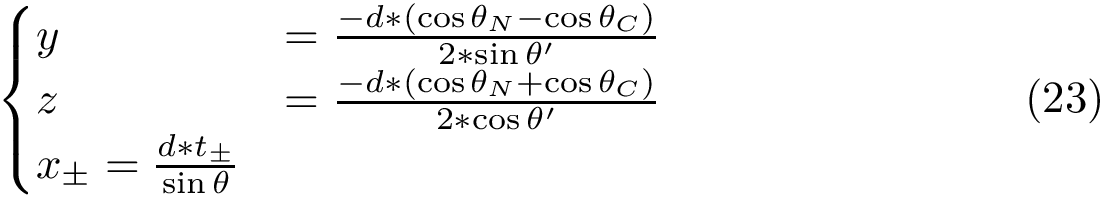
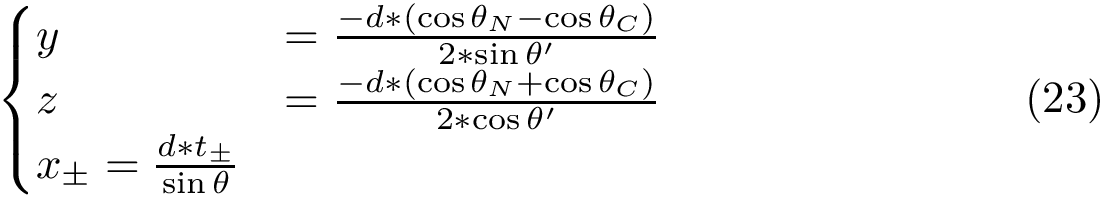
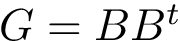

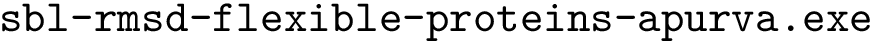
NB: the previous is sufficient when using an interpolation scheme to extend the point selected. (If the euclidean distance is used, by convexity of Voronoi regions, any point on the line-segment ![$[p_n,p_i]$](form_745.png)
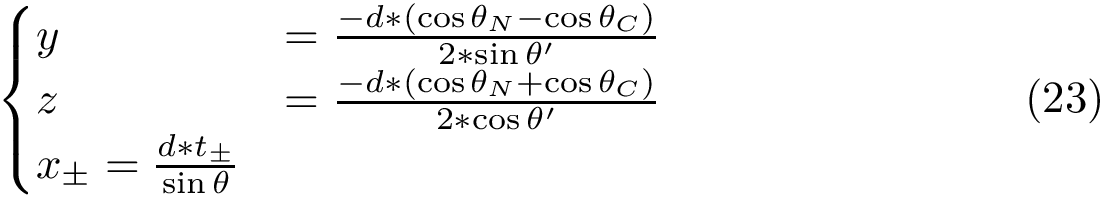
temperature adaptation taking into account the maximal energy variation of the conformational ensemble generated
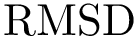
TRRT may be used to explore any model (mathematical function, toy protein model BLN, regular atomic model, etc). Since every such model yields a different executable, this executable is referred to as sbl-landexp-TRRT-NAME-OF-MODEL.exe in the sequel.
The Jupyter notebook provided in this user manual uses several such executables.
Main options.
Input.
Main output.
Identical to that of Basin-hopping, see above.
Optional output. Comments.
Intuitively, our hybrid algorithm may be seen as a variant of 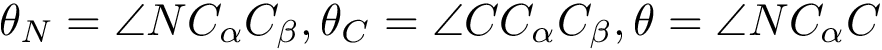
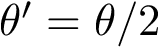
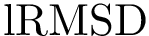
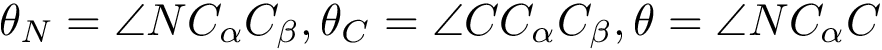
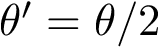
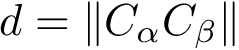
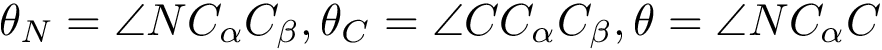
More precisely, 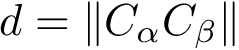
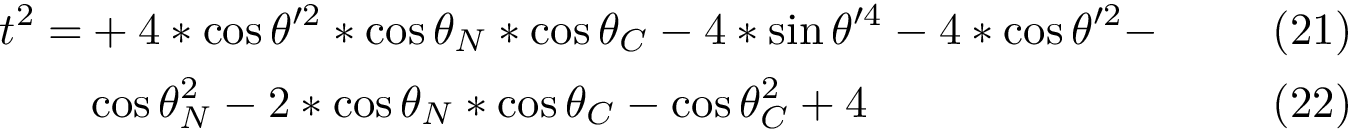
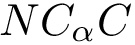
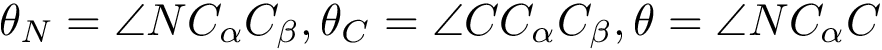
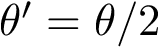
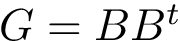
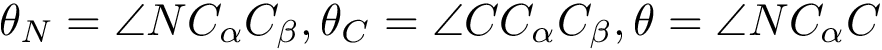

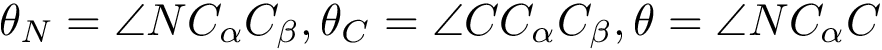
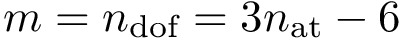
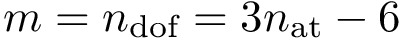
The following important remarks are in order:
The switch parameter 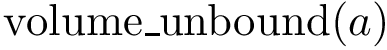
For the extension strategy, using a move set (rather than the interpolation in 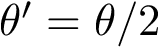
In the parameter update step, resetting the parameters upon starting a new thread is also critical, as this allows locally adapting the parameters to the landscape. Because 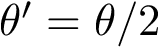
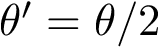
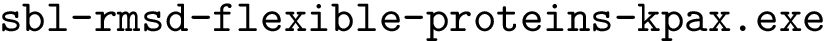
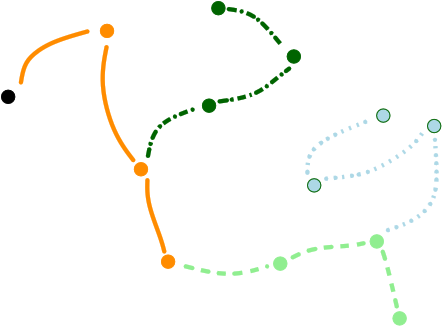 |
| The |
Hybrid may be used to explore any model (mathematical function, toy protein model BLN, regular atomic model, etc). Since every such model yields a different executable, this executable is referred to as sbl-landexp-hybrid-NAME-OF-MODEL.exe in the sequel.
The Jupyter notebook provided in this user manual uses several such executables.
Main options.
Input.
In dealing with atomic molecular models in general and proteins in particular, the following are also needed:
Main output. Whatever the system, the output files are as described previously:
Identical to that of Basin-hopping and TRRT, see above.
Optional output.
Comments.
All algorithms presented in this package follow the generic template of fig. alg-landexp-generic.
They use different ingredients, including (i) calculation of the potential energy (see packages Molecular_covalent_structure, Molecular_potential_energy) (ii) evaluation of the gradient of a real-value function (see package Real_value_function_minimizer), and (iii) spatial data structures for nearest neighbor searches (see package Spatial_search).
Note that the computation of the gradient is only semi-automatized, as mentioned in Remark. 1 of section A generic / template algorithm . In particular, the user should provide its own implementation of the gradient of the energy function, whatever is the source. An option is to use an automatic differentiation tool such as Tapenade to generate this gradient.
In addition to the usual external libraries used in the SBL (CGAL, Boost, Eigen), this package is using two other external libraries :
The programs of Landscape_explorer described above are based upon generic C++ classes, so that additional versions can easily be developed.
In order to derive other versions, there are two important ingredients, that are the workflow class, and its traits class.
T_Landscape_explorer_traits:
T_Landscape_explorer_workflow:
See the following jupyter notebook:
The exploration of an energy landscape may focus on different features:
* the extent explored
* the identification of (deep) local minima
* the identification of saddle points / transition points
In the following, we illustrate three different methods, which in a nutshell may be characterized by:
* Basin-hopping: focus on local minima -- see below
* Rapidly exploring random trees: focus on the extent visited and transition states
* Hybrid: mix between BH and T-RRT
Results are presented for the following systems:
* a complex trigonometric function defined
* BLN69, a toy protein model, whose conformation requires 3x69=207 Cartesian coordinates
* Penta-alanine, aka Ala5import re
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import squareform
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
# A Function to be used later to retrieve specific output files
def find_file_in_output_directory(str, odir):
cmd = "find %s -name *%s" % (odir,str)
return os.popen(cmd).readlines()[0].rstrip()
def plot_dendogram_of_conformations(distances):
# read the n(n-1)/2 distances and compute n
lines = open(distances, "r").readlines()
s = len(lines)
n = int((1+math.sqrt(1+8*s))/2)
# load distances into np array
mat = np.zeros((n,n))
for line in lines:
aux = re.split("\s", line.rstrip())
mat[int(aux[0]), int(aux[1])] = float(aux[2])
mat[int(aux[1]), int(aux[0])] = float(aux[2])
# plot dendogram
dists = squareform(mat)
linkage_matrix = linkage(dists, "single")
dendrogram(linkage_matrix, labels= list(range(0,n+1)))
plt.title("Conformations: dendogram based on lrmsd")
plt.show()
$ f(x,y)=(x\sin(20y)+y\sin(20x))^2\cosh(\sin(10x)x)+(x\cos(10y)-y\sin(10x))^2\cosh(\cos(20y)y)$
import matplotlib.pyplot as plt
from PIL import Image
fig, ax = plt.subplots(1, 3, figsize=(100,100))
images = ["fig/bh-trigo-50.png", "fig/trrt-trigo-50.png", "fig/hybrid-trigo-50.png"]
for i in range(0,3):
ax[i].set_xticks([]); ax[i].set_yticks([])
ax[i].imshow( Image.open(images[i]) )
print("Displayed")
The options of the runTrigo method in the next cell are:
import re #regular expressions
import sys #misc system
import os
import pdb
import shutil # python 3 only
def runTrigo(algorithm, initSample = None, movesetMode = "global", delta = 5, temperature = 2., \
tempMode = "probability", nbSamples = 10):
odir = "tmp-results-trigo-%s" % algorithm
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
program = None
if algorithm == "BH":
program = "sbl-landexp-BH-trigo-terrain.exe"
elif algorithm == "TRRT":
program = "sbl-landexp-TRRT-trigo-terrain.exe"
elif algorithm == "hybrid":
program = "sbl-landexp-hybrid-BH-TRRT-trigo-terrain.exe"
# check executable exists and is visible
exe = shutil.which(program)
if not exe:
sys.exit("Executable %s not found, exiting" % program)
print(("Using executable %s\n" % exe))
if initSample:
cmd = "%s -v1 -l --init-sample=%s \
--moveset-mode=%s --temperature=%f \
--temperature-tuning-mode=%s --nb-samples=%d --directory=%s" \
% (program, initSample, movesetMode, temperature, tempMode, nbSamples, odir)
else:
cmd = "%s -v1 -l --moveset-mode=%s \
--temperature=%f --temperature-tuning-mode=%s \
--nb-samples=%d --directory=%s" \
% (program, movesetMode, temperature, tempMode, nbSamples, odir)
if algorithm != "TRRT":
cmd += " --adaptive-displace-delta=%d" % delta
print(("Executing %s\n" % cmd))
os.system(cmd)
cmd = "ls %s" % odir
ofnames = os.popen(cmd).readlines()
print(("All output files in %s:" % odir),ofnames)
print("Marker : Calculation Started")
runTrigo("BH", initSample = "data/origin-2D.txt")
#runTrigo("TRRT", initSample = "data/origin-2D.txt")
#runTrigo("hybrid", initSample = "data/origin-2D.txt")
print("Marker : Calculation Ended")
# Retrieve the file containing the minima and samples
odir = "tmp-results-trigo-BH"
samples = find_file_in_output_directory("samples.txt", odir)
samples_energies = find_file_in_output_directory("samples_energies.txt", odir)
print("Number of samples:", os.popen( ("wc -l %s" % samples)).readlines())
minima = find_file_in_output_directory("minima.txt", odir)
minima_energies = find_file_in_output_directory("minima_energies.txt", odir)
print("Number of local minima:", os.popen( ("wc -l %s" % minima)).readlines())
Recall that BLN69 is a toy protein model made of 69 pseudo-amino acids which are either hydrophoBic, hydrophiLic,or Neutral:
from IPython.display import Image
Image(filename='fig/bln69-visu7305.jpg')
The options of the runBLN69 method in the next cell are:
import re #regular expressions
import sys #misc system
import os
import pdb
import shutil # python 3 only
def runBLN69(algorithm, ffParameters = "data/bln69.xml", initSample = None, movesetMode = "atomic", delta = 5, temperature = 2., \
tempMode = "probability", nbSamples = 10):
odir = "tmp-results-BLN-%s" % algorithm
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
program = None
if algorithm == "BH":
program = "sbl-landexp-BH-BLN.exe"
elif algorithm == "TRRT":
program = "sbl-landexp-TRRT-BLN.exe"
elif algorithm == "hybrid":
program = "sbl-landexp-hybrid-BH-TRRT-BLN.exe"
# check executable exists and is visible
exe = shutil.which(program)
if not exe:
sys.exit("Executable %s not found, exiting" % program)
print(("Using executable %s\n" % exe))
if initSample:
cmd = "%s -v1 -l --sampling-viewer vmd --ff-parameters-filename=%s --init-sample=%s \
--moveset-mode=%s --temperature=%f \
--temperature-tuning-mode=%s --nb-samples=%d --directory=%s" \
% (program, ffParameters, initSample, movesetMode, temperature, tempMode, nbSamples, odir)
else:
cmd = "%s -v1 -l --sampling-viewer vmd --ff-parameters-filename=%s --moveset-mode=%s \
--temperature=%f --temperature-tuning-mode=%s \
--nb-samples=%d --directory=%s" \
% (program, ffParameters, movesetMode, temperature, tempMode, nbSamples, odir)
if algorithm != "TRRT":
cmd += " --adaptive-displace-delta=%d" % delta
print(("Executing %s\n" % cmd))
os.system(cmd)
cmd = "ls %s" % odir
ofnames = os.popen(cmd).readlines()
print(("All output files in %s:" % odir),ofnames)
print("Marker : Calculation Started")
#runBLN69("BH", initSample = "data/bln69_global_minimum.txt")
runBLN69("TRRT", initSample = "data/bln69_global_minimum.txt")
#runBLN69("hybrid", initSample = "data/bln69_global_minimum.txt")
print("Marker : Calculation Ended")
# Retrieve the file containing the minima and samples
odir = "tmp-results-BLN-TRRT"
samples = find_file_in_output_directory("samples.txt", odir)
samples_energies = find_file_in_output_directory("samples_energies.txt", odir)
print("Number of samples:", os.popen( ("wc -l %s" % samples)).readlines())
minima = find_file_in_output_directory("minima.txt", odir)
minima_energies = find_file_in_output_directory("minima_energies.txt", odir)
print("Number of local minima:", os.popen( ("wc -l %s" % minima)).readlines())
# NB: since TRRT generates samples rather than local minima;we thus compute distances between samples
exe = shutil.which("sbl-lrmsd-all-pairs.exe")
if not exe:
print("Executable sbl-lrmsd-all-pairs.exe not found; get it from the package Molecular_distances.")
os.system( ("%s --points-file tmp-results-BLN-TRRT/sbl-landexp-TRRT-BLN__samples.txt") % exe )
plot_dendogram_of_conformations("all_distances.txt")
Let us first visuzalize this penta-peptide
from IPython.display import Image
Image(filename='fig/ala5-two-visualizations.png')
The options of the runAla5 method in the next cell are:
import re #regular expressions
import sys #misc system
import os
import pdb
import shutil # python 3 only
def runAla5(algorithm, pdb, ffType = "amber", ffParameters = "data/amber.xml", initSample = None, movesetMode = "atomic", delta = 5, temperature = 2., \
tempMode = "probability", nbSamples = 10):
odir = "tmp-results-ala5-%s" % algorithm
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
program = None
if algorithm == "BH":
program = "sbl-landexp-BH-atomic.exe"
elif algorithm == "TRRT":
program = "sbl-landexp-TRRT-atomic.exe"
elif algorithm == "hybrid":
program = "sbl-landexp-hybrid-BH-TRRT-atomic.exe"
# check executable exists and is visible
exe = shutil.which(program)
if not exe:
sys.exit("Executable %s not found, exiting" % program)
print(("Using executable %s\n" % exe))
if initSample:
cmd = "%s -v1 -l --sampling-viewer vmd --cs-pdb-files=%s --ff-type=%s --ff-parameters-filename=%s --init-sample=%s \
--moveset-mode=%s --temperature=%f \
--temperature-tuning-mode=%s --nb-samples=%d --directory=%s" \
% (program, pdb, ffType, ffParameters, initSample, movesetMode, temperature, tempMode, nbSamples, odir)
else:
cmd = "%s -v1 -l --sampling-viewer vmd --cs-pdb-files=%s --ff-type=%s --ff-parameters-filename=%s --moveset-mode=%s \
--temperature=%f --temperature-tuning-mode=%s \
--nb-samples=%d --directory=%s" \
% (program, pdb, ffType, ffParameters, movesetMode, temperature, tempMode, nbSamples, odir)
if algorithm != "TRRT":
cmd += " --adaptive-displace-delta=%d" % delta
print(("Executing %s\n" % cmd))
os.system(cmd)
cmd = "ls %s" % odir
ofnames = os.popen(cmd).readlines()
print(("All output files in %s:" % odir),ofnames)
print("Marker : Calculation Started")
#runAla5("BH", pdb="data/ala5.pdb", initSample = "data/ala5.txt")
#runAla5("TRRT", pdb="data/ala5.pdb", initSample = "data/ala5.txt")
runAla5("hybrid", pdb="data/ala5.pdb", initSample = "data/ala5.txt", nbSamples = 50)
print("Marker : Calculation Ended")
# Retrieve selected files
odir = "tmp-results-ala5-hybrid"
samples = find_file_in_output_directory("samples.txt", odir)
samples_energies = find_file_in_output_directory("samples_energies.txt", odir)
print("Number of samples:", os.popen( ("wc -l %s" % samples)).readlines())
minima = find_file_in_output_directory("minima.txt", odir)
minima_energies = find_file_in_output_directory("minima_energies.txt", odir)
print("Number of local minima:", os.popen( ("wc -l %s" % minima)).readlines())
Note that sbl-lrmsd-all-pairs.exe from Molecular_distances
exe = shutil.which("sbl-lrmsd-all-pairs.exe")
if not exe:
print("Executable sbl-lrmsd-all-pairs.exe not found; get it from the package Molecular_distances.")
os.system( ("%s --points-file tmp-results-ala5-hybrid/sbl-landexp-hybrid-BH-TRRT-atomic__minima.txt") % exe)
plot_dendogram_of_conformations("all_distances.txt")