Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Table of Contents

Authors: F. Cazals and T. Dreyfus and D. Mazauric and C. Roth

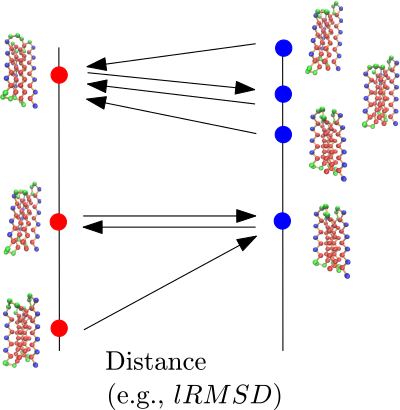
Conformational_ensemble_comparison

This package provides methods to compare, from a geometric/structural standpoint, two ensembles of conformations.

Goals

Consider two conformational ensembles, also called samplings, as defined in section Conformational ensembles – aka samplings . Let 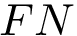$\dCalC{\cdot}{\cdot}$ be some distance between two conformations.

This package offers methods two compare these two ensembles in different ways:

  • comparing the two ensembles using minimum spanning forests,
  • computing the symmetric difference and the intersection between two samplings,

  • computing the Hausdorff distance between ensembles

These functionalities are provided in the program 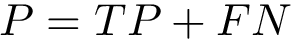$\sblCECL$.

Using sbl-conf-ensemble-comparison-lrmsd.exe

Pre-requisites

Minimum spanning forests

A standard problem in analyzing ensembles of conformations consists of comparing two such ensembles. For example, one may wish to compare two sets of local minima, or two sets of structures selected for their relevance in a particular context.

To perform such an assessment, consider two sets of conformations, denoted for convenience 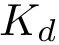$R$ (say the reference set), and $C$. In the sequel, we consider a comparison criterion involving one distance for each conformation from $C$ and $R$.

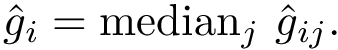
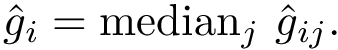
We do so by computing a minimal spanning forest of a weighted complete bipartite graph induced by the two sets 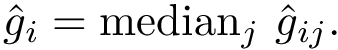$C$ and $R$. More precisely, the nodes represent the conformations and there is an edge between every node representing a conformation $c\in C$ and every node representing a conformation $r\in R$. The weight of an edge is the distance $\dCalC{r}{c}$. The problem then consists of computing a minimum weight subset of edges such that every node of the bipartite graph is incident to at least one edge of this subset. This means that every conformation is associated with at least another one. More precisely, considering the aforementioned spanning forest as directed, each conformation is constrained to have exactly one outgoing edge, connecting it to the nearest conformation.

Note that the following pieces of information are returned:

  • High level statistics: the sum of weights of oriented arcs.

  • Low level statistics: the list of oriented edges and their weight that is a list of triples.

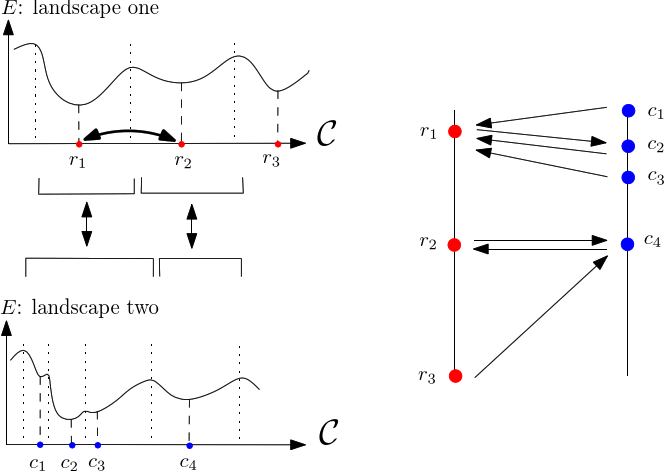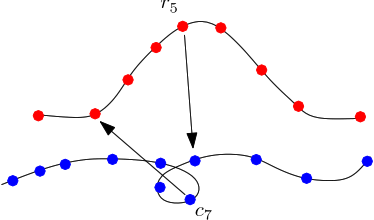
Comparing sets of minima using a Minimum Oriented Spanning Forest (MSF)
Each conformation from a sampling picks the nearest neighbor in the second set. Note that the process is not symmetric: $r_3$ picks $c_4$, but $c_4$ picks $r_2$.

Hausdorff distance between ensembles

To get a global criterion, we introduce the so-called Hausdorff distance, a 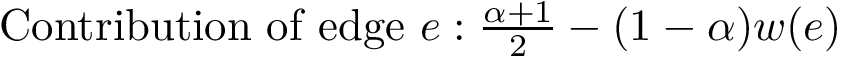$\max\min$ type criterion.

Consider the previous sets of conformations 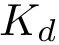$R$ and $C$. To assess the coverage of the set $R$ by $C$, we compute for every sample $r\in R$ its nearest neighbor in $C$:

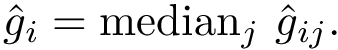
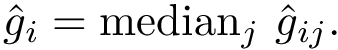
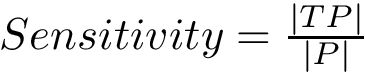
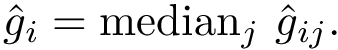
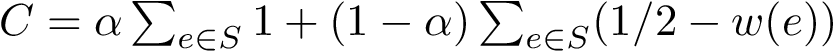
$ \forall r\in R: d(r, C) = \min_{c\in C} \dCalC{r}{c}. $

We then report the following triple:

$ \text{min}_{r\in R} d(r,R), \text{median}_{r\in R} d(r,R), \text{max}_{r\in R} d(r,R). $

Note that the third entry in Eq. (eq-hausdorff-triple) is the so-called one-sided Hausdorff distance between $R$ and $C$ – the sample from $R$ which is the most isolated from $C$.

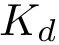
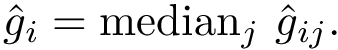
One sided Hausdorff distance
Given two sets of conformations, one seeks for each of them the sample located furthest in the second sampling. Maximizing this distance yields the one sided Hausdorff distance.

Intersection and symmetric difference

Given two samplings 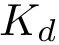$R$ and $C$, two useful operations are to compute

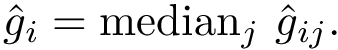
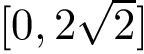
  • the intersection $R\cap C$,

  • the symmetric difference $R\Delta C$: $R\backslash C$ and $C\backslash R$.

Note that the previous set operations are performed up to a user-specified tolerance 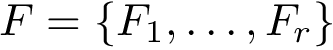$tol$ on the distance $\dCalC{\cdot}{\cdot}$.

Input: Specifications and File Types

The input is two conformational ensembles of the same molecule, and can be provided with several format:

  • Conformation file: the input is a file listing each conformation as a D-dimensional point, i.e the dimension of the conformation followed by the (x, y, z) coordinates of all the atoms, just separated by a blank 
    6 x11 y11 z11 x12 y12 z12
6 x21 y21 z21 x22 y22 z22
6 x31 y31 z31 x32 y32 z32
...
  • Gromacs xtc file: the input is a file generated by the Gromacs software

All comparisons are optional, so that they have to be specified in the command-line. For example, running Hausdorff comparison is done using the option –Hausdorff. Thus, a calculation is launched as follows:

> sbl-conf-ensemble-comparison-lrmsd.exe --points-file data/bln69_sampling.txt --points-file data/bln69_10_lowest_minima.txt --Hausdorff --symmetric-difference --identity-threshold 0.01 --exact-search --directory results --verbose --output-prefix --log
The main options of the program $\sblCECL$ are:
–points-file string: plain text file listing all conformations of one ensemble as D-dimensional points
–Hausdorff: run Hausdorff distance based comparison
–symmetric-difference: run comparison by computing intersection and symmetric difference ofthe two ensembles
–identity-threshold float(= 0.00001): threshold under which two conformations are considered identical
–exact-search: run brut force algorithm for searching nearest neighbors


File Name

Description

BLN69 conformations file Sampling done from sbl-landexp-hybrid-BH-TRRT-BLN.exe
BLN69 conformations file

Ten lowest local minima of BLN69 obtained by an external sampling method

Input files for the run described in section Input: Specifications and File Types .

Output: Specifications and File Types

PreviewFile Name

Description

General: log file

Log file

Log file containing high level information on the run of $\sblCECL$

Module MSF analysis: Minimum spanning forest

Conformation matches text file

List of edges of the MSF with the distance between the selected conformations

Module symmetric difference analysis: intersection and symmetric difference

Conformation matches text file

List the pair of indices of conformations that match

Output files for the runs described in section Input: Specifications and File Types, classified by modules – see Fig. fig-cec-workflow .

Algorithms and Methods

Minimum spanning forests

It is easily shown that an optimal subset of edges induces a forest; i.e., a subgraph without cycles. A simple algorithm consists of choosing, for every node, the incident edge with the smallest weight. This strategy corresponds to the first step of 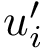$\text{\boruvka}$'s algorithm for computing a minimum spanning tree in a graph [134] . (See also Boruvka's algorithm.) Note that if the weights are not all different, a correction step is necessary in order to avoid cycles.

Two strategies are offered to compute the nearest neighbor of each sample:

  • Brute force: a linear scan is used to find the exact nearest neighbor.

  • Approximate: data structures to perform approximate nearest neighbor searches are used, see package Spatial_search

Hausdorff distance between ensembles

The nearest neighbor of each sample is computed during the MSF calculations. This information is used to compute the Hausdorff triple of Eq. eq-hausdorff-triple.

Programmer's Workflow

The programs of Conformational_ensemble_comparison described above are based upon generic C++ classes, so that additional versions can easily be developed.

In order to derive other versions, there are two important ingredients, that are the workflow class, and its traits class.

The Traits Class

T_Conformational_ensemble_comparison_traits:

The Workflow Class

T_Conformational_ensemble_comparison_interface_workflow: