User Manual

Table of Contents

• Introduction
• Algorithms
• Implementation and functionalities
• Design and classes
• Examples

Rotation_3

Authors: F. Cazals and T.O'Donnell

Introduction

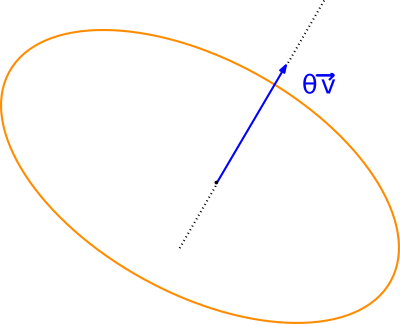
There are several ways to define and parameterize 3D rotations, see e.g. Wiki/rotation in 3D and Wiki/rotation matrix :

• Euler angles: the rotation is decomposed into three simpler rotations
• Angle-axis: the rotation is parameterized by a rotation around an arbitrary axis. (Nb: the set of all rotations is typically referred to as the -ball.)
• Matrices representing the special orthogonal group SO(3).
• Quaternions, which generalize complex numbers in 3D.

This package provides various parameterization of rotations using these formalisms, using low level classes from Eigen.

Algorithms

Implementation and functionalities

The reader is referred to [8] as well as rotations 3D formalism and rotation matrix .

We also note in passing that there exist various metrics between 3D rotation, see [114] and [98] .

Design and classes

3D Rotations are performed on points trough a single overloaded functor templated by a number type: SBL::GT::T_Rotation_3

This class takes in as input from one to three angular radii values followed by the same number of orthogonal axes around which the corresponding rotations are applied. If no axes are given the unity vectors x y and z are used by default(in this order). Varying representations of 3 dimensional rotation can be obtained through methods of SBL::GT::T_Rotation_3:

• Quaternions (Eigen::Quaternion<NT>)
• Angle and axis(Eigen::AngleAxis<NT>)
• 3D rotation matrix(Eigen::Matrix<NT,3,3>)

The functor operator needs an iterator input for points and an iterative output to apply the rotation directly. Finally if on top of all the previous parameters a center of rotation is supplied then the points will be centered before rotation is applied.

Examples

The following examples shows how to rotate a set of randomly drawn 3D points: