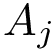Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Table of Contents

Iterative_alignment

Authors: F. Cazals and T. Dreyfus and R. Tetley

Introduction

Structural alignments.

Given two structures, a structural alignment is a matching between structural motifs within these structures. The problem has many variants, depending on (i) the representation used, (ii) the score optimized, and (iii) the optimization algorithm used.

As typical examples, one may cite:

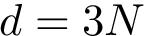
  • $\text{\apurva}$ is a structural aligner based on contact maps, favoring long and flexible alignments [11] – see Apurva.
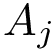
  • $\text{\kpax}$ is a structural aligner based on a geometric representation of the backbone, favoring a geometric measure known as the G-score [151] .

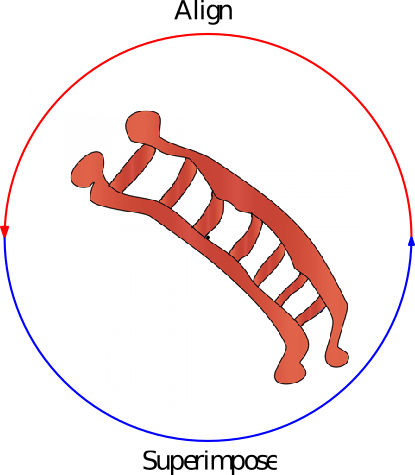
Iterative alignments. Iterative alignments [24] , [151] consists in iteratively finding the alignment for fixed positions of the conformations–via dynamic programming, and finding optimal superimposition given the alignment–the classical rigid superimposition problem. The process is typically iterated until a fixed point or a cycle is reached. Such alignments are especially interesting when seeded with our motifs, for two reasons.

Performing a structural alignment has two components:

  • Pairing amino-acids,
  • Performing a rigid superimposition given a pairing.

Each step is easy given the result of the other one:

  • Paring amino-acids given fixed positions for the molecules can be solved via dynamic programming.
  • Performing a rigid superimposition given a pairing can be solved by computing the rigid motion minimizing the RMD deviation – using say a SVD calculation.

The complexity actually comes from solving these two steps at once. To do so, a classical strategy consists in interleaving the DP two operations just discussed.

This is used in the fuzzy alignment from [24] , and also for 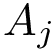$\text{\kpax}$ [151] .

Alignments and statistics. The companion package Alignment_engines provides tools to compute statistics on various alignments.

Implementation and functionalities

The Iterative_alignment package provides a number of novel classes to ease the instantiation of novel aligners – see e.g. the package Kpax .

  • SBL::CSB::T_Iterative_aligner<class StructureType , class SeederType , class ScoreComputer > This class provides the aligner itself. The user must provide an alignment structure type through the parameter StructureType (also see the package Alignment_engines), as well as a seeder ( SeederType ) and a score computer ( ScoreComputer ). Note that this package provides a default instantiation of the aligner in the Kpax algorithm.
  • SBL::CSB::T_Seeder_DP_score<class StructureType , ScoreComputer > The Kpax algorithm [151] also uses a DP approach to compute the alignment seed. This class provides a generic implementation of this approach, allowing users to build their own seeder by providing a StructureType and ScoreComputer which will use a different score than Kpax.
  • SBL::CSB::T_Canonize_conformation<class CovalentStructure , ConformationType > This class provides a functor allowing to compute canonized conformations (as explained in [151] . The parameter CovalentStructure is the representation of the polypeptide chain covalent structure, and ConformationType is the representation of its 3-dimensionnal conformation.

Examples

The classes from this package and those from the package Alignment_engines are used to implement the $\text{\kpax}$ algorithm, see Kpax .