Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Lie_group_interpolation

Authors: F. Cazals and A. Jha

Introduction

Algorithms

Implementation and functionalities


Classes.

SBL::GT::T_SE3_representation

Internally represented by a 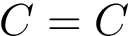$3x3$ rotation matrix, and the translation vector.

SBL::GT::T_SO3_representation : inherits from SBL::GT::T_SE3_representation; add in particular distances for rotations, see [108]

SBL::GT::T_SE3_motion : between 2 given frames

Consider an initial frame 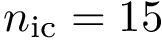$(c_1, F_1)$ – with $c_1$ the frame location/origin and $F_1$ the orthonormal basis in matrix form; likewise, let $(c_2, F_2)$ be a target frame.

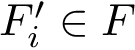
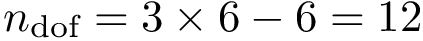
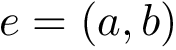
The rotation matrix 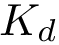$R$ bringing $F_1$ onto $F_2$ reads as $R = F_2 \transpose{F_1}$. Therefore, the transformation mapping a point $x$ from the first frame into the second one satisfies

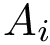
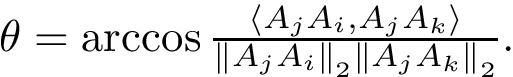
\begin{equation}x' = R(x-c_1) + c_2 \end{equation}

or equivalently

\begin{equation}x' = F_2 \transpose{F_1} (x-c_1) + c_2. \end{equation}

The previous formulae is easily understood:

  • the product $\transpose{F_1} (x-c_1) $ expresses the vector $x-c_1$ in the base $F_1$,
  • the product with $F_2$ rewrites the previous vector in the base $F_2$,
  • the addition of $c_2$ make the origin of $F_1$ coincide with that of $F_2$.

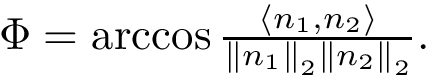
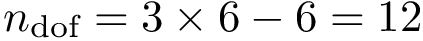
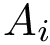
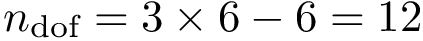
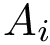
SBL::GT::T_Trajectory : position of a point in a frame moved by a SE3 motion


Critical operations /numerics. The major mathematical operations involved in interpolation are the matrix exponential and logarithms, for which closed form expressions are known [84] [83] . These closed form expressions involve the usage of trigonometric functions, which are evaluated using the number type CGAL::Gmpfr number type.

Furthermore,

  • The get_theta function, which operates on a skew-symmetric matrix, is supposed to deliver a number \eql{}. This property is asserted.
  • The case $\theta=\pi$, as discussed in [84] is problematic – see paragraph after Eq. (11). To be polished.
Trigonometric internal calculations deliver numbers of type CGAL::Gmpfr. Internally, interval arithmetic calculations are carried out – with MPFI or Boost, see SBL::GT::Trigonometric_interval_kernel.


A useful resource to navigate between the various representations available for rotations is the rotations converter .


Using

The program 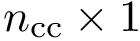$\text{\codecx{sbl-lie-interpolator.exe}}$ offers functionalities to interpolate between two rigid motions.


Input. A spec file with 2 points on SE3, using the following syntax:

screw motion via one translation + one rotation screw motion via the specification of two frames

// Syntax for translation only: 
letter t + 3 numbers denoting the translation vector (x,y,z)
t tx tx tz


// Syntax for quaternion representation: 
letter q + 3 numbers denoting the translation component + 4 numbers denoting the quaternion 
component
q tx ty tz qu qv qw qz

// Syntax for angle axis representation: 
letter a + 3 numbers denoting the translation component + 3 numbers denoting the unit vector 
+ 1 number denoting the angle
a tx ty tz ux uy uz alpha

// Syntax for angle axis (polar): 
letter a + 3 numbers denoting the translation component + 2 numbers denoting the angles 
(theta,phi) for the unit vector + 1 number denoting the angle
a tx ty tz theta phi alpha

// Syntax for frame presentation: 2 frames; each represented by its center + 2 vectors
(it is assumed that the third vector is the cross product of the first two vectors)
f px1 py1 pz1 ux1 uy1 uz1 vx1 vy1 vz1  qx2 qy2 qz2  ux2 uy2 uz2 vx2 vy2 vz2

// Syntax for 2-vector specification of rotation: letter f + 3  numbers denoting the center of frame 1 
+ 3 numbers denoting the center of frame 2 + 2 numbers denoting the angles for the first vector of frame 1 
+ 2 numbers denoting the angles for the second vector of frame 2 + 2 numbers denoting the angles for 
the first vector of frame 2 + 2 numbers denoting the angles for the second vector of frame 2
(it is assumed that the third vector is the cross product of the first two vectors)
f px1 py1 pz1 qx2 qy2 qz2 u_theta1 u_phi1 v_theta1 v_phi1 u_theta2 u_phi2 v_theta2 v_phi2

// Comments can be added by starting the line with a #
# Comment-Line


Output. File for meshlab

pi/2 rotation

t 0 0 0
f 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 -1 0 0
f 0 0 0 1 0 0 0 1 0 0 0 0 -1 1 0 1 1 0
f 1 2 3 1 0 0 0 1 0 2 3 5 -1 0 0 0 1 0


Interpolating between two rigid motions, each defined by a frame in this case. Ply file generated with the command 
./sbl-lie-interpolator.exe --input data/moving-between-two-frames.txt --n 100