 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: A. Sales-de-Queiroz and G. Sales Santa Cruz and A. Jean-Marie and D. Mazauric and J. Roux and F. Cazals
Single cell RNA sequencing. Single cell RNA sequencing (scRNAseq) consists of (i) dissociating cells in a tissue, (ii) performing cell isolation, (iii) extracting mRNA and amplifying them, and (iv) counting the number of transcripts on a per gene basis.
Ideally, scRNAseq allows one to bridge the gap between expression profiles a single cell phenotypes. This endeavor is however especially challenging for two main reasons; first, the cells processed may occupy a wide variety of cell states; second, the low mRNA counts on a per cell basis are such that a number of genes may be missed – the drop-out phenomenon.
A classical analysis performed on scRNAseq is the identification of deferentially expressed genes. A number of different techniques have been developed for it, see [194].

A complementary type of analysis ambitions to understand which DE genes interact with a specific molecular pathway, e.g. that of apoptosis. More specifically, consider the following triple:
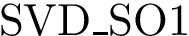
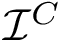
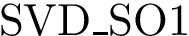
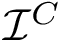
In this work, we address the problem of prioritizing the genes in 
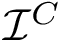
The tool developed to do so is called 
In the following, we provide an intuitive presentation of 
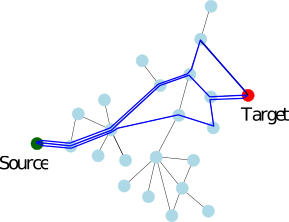
We consider a PPIN whose vertices are the individual molecules, and whose edges represent pairwise interactions. Such a network is modeled by a vertex-weighted edge-weighted directed graph 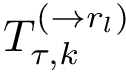
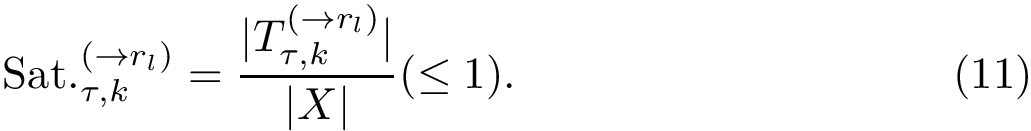
To present the formalism, the two sets of nodes are denoted 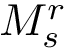
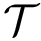

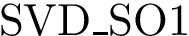
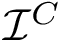
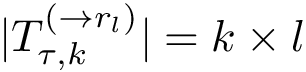
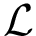
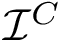
Consider:
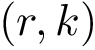
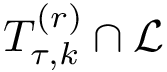
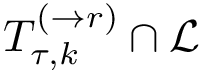
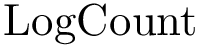
We assume that the reader/user is acquainted with the following concepts, see e.g. [27] :
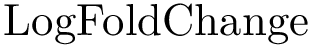
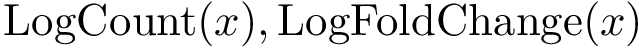
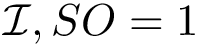
Random walks on graphs are best studied using the framework of Markov chains. Recall that a Markov chain is a stochastic processes visiting states. In our case, the states are the vertices of the graph, and the transition probabilities are encoded in a transition matrix, whose non null entries correspond to the edges 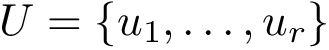
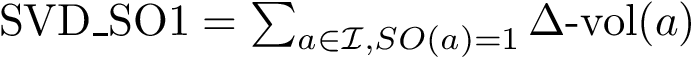
Hit vectors and hit scores.. After a number of steps of the random walk:
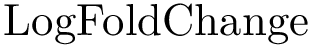
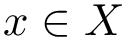


![\begin{equation}\grwsd[M^{r}_{S'}]^{i} = (\grwsd[M^{r}_{S'}]^{i}(v_{1}),\dots,\grwsd[M^{r}_{S'}]^{i}(v_{n}) ),
\end{equation}](form_598.png)
![$\grwsd[M^{r}_{S'}]^{0}(u) = 0$](form_599.png)
![$\grwsd[M^{r}_{S'}]^{0}(u) = \frac{1}{|S'|}$](form_601.png)

Under suitable hypothesis, the previous quantities admit a limit when 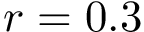

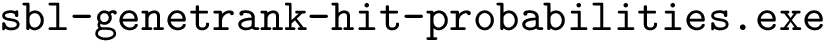
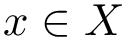

![$\grwsd[M^{r}_{S'}] = (\grwsd[M^{r}_{S'}](t_{1}),\dots,\grwsd[M^{r}_{S'}](t_{k}))$](form_606.png)
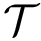
Note that in the previous definition, 
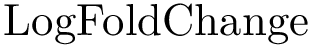

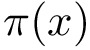

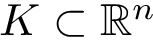
![$\grwsd[M]{t}$](form_612.png)
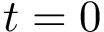
Finally, we define the hit score, based on the hit probability, and the centrality of a node measured by ![$\grwsd[M]{t}$](form_612.png)
![$r \in [0,1]$](form_613.png)
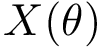
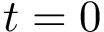
![\begin{equation}\scoredir{s}{t} = \grwsd[M^{r}_s]{t} / \grwsd[M]{t},
\end{equation}](form_614.png)

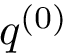

Instances (PPIN, 
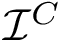
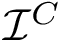
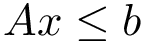
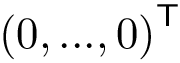
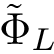
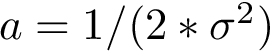
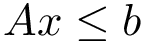
Symmetry. To analyse the (lack of) symmetry between paths joining 
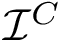

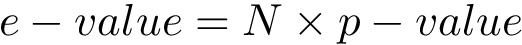
Using the hit scores in the two directions 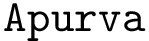
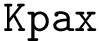
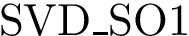
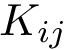
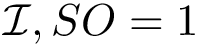
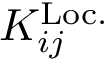
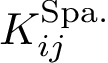
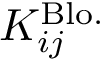


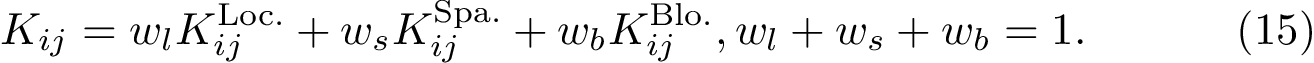
Note that when 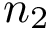
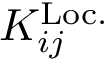
To assess the stability of this ranking, we proceed as follows. Consider a set of values 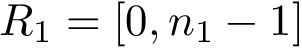
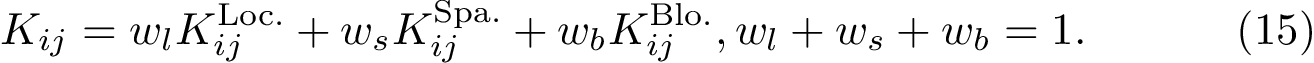
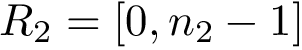
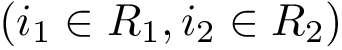
We now use this set to qualify the speed at which we discover the sources in 
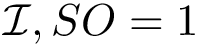
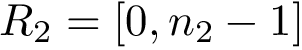
In the absence of overlap between consecutive 

We note in passing that the previous sets can be used to define how many hits in a given reference list of genes 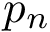
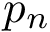
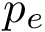

Expression levels and fold-changes for genes in 
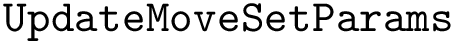
Score radar plots. The difficulty in working with values 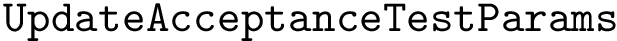

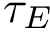

Each gene score radar plot is defined as follows:
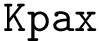

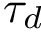
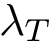
Score radar scatter plot. Displaying all individual score radar plots in the 
NB: While the Markov chain and score calculations in identifier-type agnostic, the generation of gene radars, and gene radar scatters, assumes that the identifiers used are protein identifiers, and could fail if another type of identifier is used.
Genes versus proteins. In the sequel, we manipulate genes and proteins. The following formats are used:
Protein Protein Interaction Network – PPIN. The PPIN file should be a tab-separated file of interactions, where each interaction has the two protein identifiers, and a weight ![$(0, 1]$](form_653.png)
NB: These interactions are bidirectional ie give rise to arcs in both directions, whence two non null entries in the Markov chain transition matrix.
Gene set 
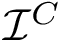
Example: 5 sources used [68]
Example: 51 sources used [68]
Markov models and hit scores..
We compute hit scores (Def. def-hit-score) using the C++ 
For a given restart rate, we output a csv file containing the scores 
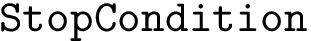

Example: results file for the whole MINT PPIN, obtained for 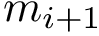
Reranked gene lists. Our final product is the set of top genes defined by 
These set depend on three parameters:
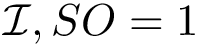
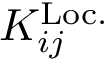

We output such lists in plain txt files.
Radar plots.
We assume a MA plot file, containing triples (gene id, logFC, logCPM).
The radar plots are obtained using this file and the reranked gene list file.
 |
| Example radar plot. |
 |
| The radar scatter plot combining the individual radar plots. |
The package proves two executables compiled from C++ programs, and three python scripts. We now briefly describe these programs, and refer the user to the Jupyter notebook for example calls.
C++ based executables.
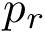
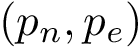
Python scripts.
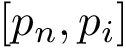
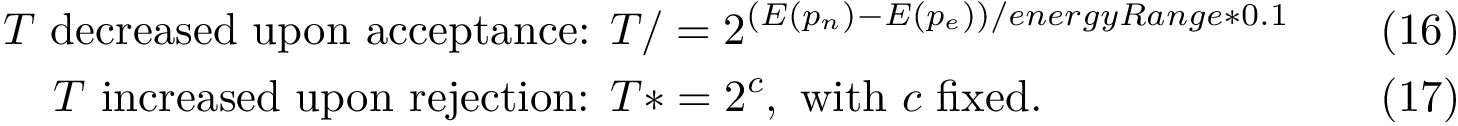


As noticed above, Markov models rely on the C++ 
To use this package, proceed as follows:
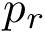
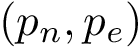
See the following jupyter notebook:
import os
import subprocess
import shutil
from SBL import SBL_pytools
from SBL_pytools import SBL_pytools as sblpyt
from SBL import SBL_Genetrank_application
from SBL_Genetrank_application import Genetrank_application
from SBL import SBL_Genetrank_gene_to_protein
from SBL_Genetrank_gene_to_protein import *
genes = [line.rstrip() for line in open("data/proteins-targets-apoptosis-49-entries.in").readlines()]
print(genes)
translator = Genetrank_GeneProteinTranslator('hsapiens', direction='protein2gene')
translations = translator.translate(genes)
print(translations)
translations.summary()
['O43464', 'P19438', 'Q07817', 'O43521', 'D3DV04', 'P20333', 'Q13489', 'Q6FH21', 'P55211', 'O95831', 'Q13794', 'Q15628', 'Q8IX12', 'P98170', 'P55957', 'Q8WZ73', 'Q86W13', 'O14763', 'Q13618', 'Q07812', 'P62877', 'Q13546', 'Q9UMX3', 'P55210', 'O14798', 'Q9BXH1', 'O15392', 'Q13158', 'Q9NZS9', 'P21580', 'Q92843', 'O15519', 'P08574', 'P42575', 'P10415', 'O00198', 'O00220', 'Q92851', 'Q8WXG6', 'Q16611', 'Q13323', 'Q96LC9', 'Q13490', 'Q9NR28', 'P42574', 'Q14790', 'Q9UBN6', 'P25445', 'O14727'] Succesful Translations: O43464: HTRA2 P19438: TNFRSF1A Q07817: BCL2L1 O43521: BCL2L11 P20333: TNFRSF1B Q13489: BIRC3 P55211: CASP9 O95831: AIFM1 Q13794: PMAIP1 Q15628: TRADD Q8IX12: CCAR1 P98170: XIAP P55957: BID Q8WZ73: RFFL O14763: TNFRSF10B Q13618: CUL3 Q07812: BAX P62877: RBX1 Q13546: RIPK1 Q9UMX3: BOK P55210: CASP7 O14798: TNFRSF10C Q9BXH1: BBC3 O15392: BIRC5 Q13158: FADD Q9NZS9: BFAR P21580: TNFAIP3 Q92843: BCL2L2 O15519: CFLAR P08574: CYC1 P42575: CASP2 P10415: BCL2 O00198: HRK O00220: TNFRSF10A Q92851: CASP10 Q8WXG6: MADD Q16611: BAK1 Q13323: BIK Q96LC9: BMF Q13490: BIRC2 Q9NR28: DIABLO P42574: CASP3 Q14790: CASP8 P25445: FAS O14727: APAF1 Ambiguous Translations: Unable to Translate: D3DV04 Q6FH21 Q86W13 Q9UBN6 Of 49 identifiers: 45 successfully translated 0 ambiguously translated 4 unable to be translated
from SBL import SBL_Genetrank_application
from SBL_Genetrank_application import Genetrank_application
from SBL import SBL_pytools
from SBL_pytools import *
odir = "test5s"
if os.path.exists(odir):
pass
#os.system( ("rm -rf %s" % odir))
os.system( ("mkdir -p %s" % odir))
ppin_file_path = 'data/MINT-human-august2020.in'
sources_file_path = 'data/proteins-sources-5-entries.in'
targets_file_path = 'data/proteins-targets-apoptosis-49-entries.in'
pathways_dir_path = '/tmp/pathways'
os.mkdir(pathways_dir_path)
app = Genetrank_application(odir)
app.add_ppin_file(ppin_file_path)
app.add_sources_file(sources_file_path)
app.add_targets_file(targets_file_path)
app.add_pathways_dir(pathways_dir_path)
app.add_restart_probability(0.01)
app.add_restart_probability(0.3)
app.generate_inputs()
app.instantiate_simulations()
def odir_tree(highlight_pattern='^'):
cmd = "tree %s | grep --color=always -e '^' -e '%s'" % (odir, highlight_pattern)
tree = ''.join(os.popen(cmd).readlines())
return tree
Uses the executable sbl-genetrank-Markov-models.exe to generate the Markov Chain .mcl transition matrix files to be used by MARMOTE. These files are one per source, named mcr_<internal_source_id>.mcl. markov_chain.mcl contains the normalization Markov Chain's transition matrix.
source_idx.txt, target_idx.txt, and map_protein_name_idx.txt are also produced to be used to cross-reference the identifiers used internally by the executable with the protein identifiers.
app.generate_markov_chains()
print(odir_tree('*.mcl'))
Creating directory for r=0.01 (cmd=mkdir -p test5s/r0.01)
Creating directory for r=0.30 (cmd=mkdir -p test5s/r0.30)
Generating Markov Chains (one for each source)...
PPIN = MINT-human-august2020
SOURCES = proteins-sources-5-entries
TARGETS = proteins-targets-apoptosis-49-entries
r = 0.01
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-Markov-models.exe -g data/MINT-human-august2020.in -p /tmp/pathways -s data/proteins-sources-5-entries.in -t data/proteins-targets-apoptosis-49-entries.in -r 0.01 -o test5s/r0.01
Generating Markov Chains (one for each source)...
PPIN = MINT-human-august2020
SOURCES = proteins-sources-5-entries
TARGETS = proteins-targets-apoptosis-49-entries
r = 0.30
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-Markov-models.exe -g data/MINT-human-august2020.in -p /tmp/pathways -s data/proteins-sources-5-entries.in -t data/proteins-targets-apoptosis-49-entries.in -r 0.30 -o test5s/r0.30
...Markov Chains generated.
(they can be found at test5s/r0.30/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30)
...Markov Chains generated.
(they can be found at test5s/r0.01/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01)
Creating directory for r=0.01 (cmd=mkdir -p test5s/r0.01)
Creating directory for r=0.30 (cmd=mkdir -p test5s/r0.30)
Generating Markov Chains (one for each source)...
Generating Markov Chains (one for each source)... PPIN = MINT-human-august2020
SOURCES = proteins-targets-apoptosis-49-entries
TARGETS = proteins-sources-5-entries
r = 0.01
PPIN = MINT-human-august2020
SOURCES = proteins-targets-apoptosis-49-entries
TARGETS = proteins-sources-5-entries
r = 0.30
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-Markov-models.exe -g data/MINT-human-august2020.in -p /tmp/pathways -s data/proteins-targets-apoptosis-49-entries.in -t data/proteins-sources-5-entries.in -r 0.01 -o test5s/r0.01 Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-Markov-models.exe -g data/MINT-human-august2020.in -p /tmp/pathways -s data/proteins-targets-apoptosis-49-entries.in -t data/proteins-sources-5-entries.in -r 0.30 -o test5s/r0.30
...Markov Chains generated.
(they can be found at test5s/r0.30/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30)
...Markov Chains generated.
(they can be found at test5s/r0.01/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01)
test5s
├── figures
│ └── r0.30
├── r0.01
│ ├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_2437.mcl
│ │ ├── mcr_3187.mcl
│ │ ├── mcr_3480.mcl
│ │ ├── mcr_420.mcl
│ │ ├── mcr_679.mcl
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ └── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_10406.mcl
│ ├── mcr_10715.mcl
│ ├── mcr_1560.mcl
│ ├── mcr_2123.mcl
│ ├── mcr_2292.mcl
│ ├── mcr_2743.mcl
│ ├── mcr_2777.mcl
│ ├── mcr_2823.mcl
│ ├── mcr_2995.mcl
│ ├── mcr_3584.mcl
│ ├── mcr_3585.mcl
│ ├── mcr_385.mcl
│ ├── mcr_4131.mcl
│ ├── mcr_4132.mcl
│ ├── mcr_4158.mcl
│ ├── mcr_4407.mcl
│ ├── mcr_4686.mcl
│ ├── mcr_4930.mcl
│ ├── mcr_4932.mcl
│ ├── mcr_5157.mcl
│ ├── mcr_5201.mcl
│ ├── mcr_5251.mcl
│ ├── mcr_5252.mcl
│ ├── mcr_5266.mcl
│ ├── mcr_5296.mcl
│ ├── mcr_5326.mcl
│ ├── mcr_5499.mcl
│ ├── mcr_551.mcl
│ ├── mcr_560.mcl
│ ├── mcr_5668.mcl
│ ├── mcr_5770.mcl
│ ├── mcr_699.mcl
│ ├── mcr_722.mcl
│ ├── mcr_7333.mcl
│ ├── mcr_8055.mcl
│ ├── mcr_8223.mcl
│ ├── mcr_8226.mcl
│ ├── mcr_858.mcl
│ ├── mcr_868.mcl
│ ├── mcr_9210.mcl
│ ├── mcr_9945.mcl
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── r0.30
├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_2437.mcl
│ ├── mcr_3187.mcl
│ ├── mcr_3480.mcl
│ ├── mcr_420.mcl
│ ├── mcr_679.mcl
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30
├── map_protein_name_idx.txt
├── markov_chain.mcl
├── mcr_10406.mcl
├── mcr_10715.mcl
├── mcr_1560.mcl
├── mcr_2123.mcl
├── mcr_2292.mcl
├── mcr_2743.mcl
├── mcr_2777.mcl
├── mcr_2823.mcl
├── mcr_2995.mcl
├── mcr_3584.mcl
├── mcr_3585.mcl
├── mcr_385.mcl
├── mcr_4131.mcl
├── mcr_4132.mcl
├── mcr_4158.mcl
├── mcr_4407.mcl
├── mcr_4686.mcl
├── mcr_4930.mcl
├── mcr_4932.mcl
├── mcr_5157.mcl
├── mcr_5201.mcl
├── mcr_5251.mcl
├── mcr_5252.mcl
├── mcr_5266.mcl
├── mcr_5296.mcl
├── mcr_5326.mcl
├── mcr_5499.mcl
├── mcr_551.mcl
├── mcr_560.mcl
├── mcr_5668.mcl
├── mcr_5770.mcl
├── mcr_699.mcl
├── mcr_722.mcl
├── mcr_7333.mcl
├── mcr_8055.mcl
├── mcr_8223.mcl
├── mcr_8226.mcl
├── mcr_858.mcl
├── mcr_868.mcl
├── mcr_9210.mcl
├── mcr_9945.mcl
├── source_idx.txt
├── source_names.txt
└── target_idx.txt
8 directories, 112 files
Uses the executable sbl-genetrank-hit-probabilities.exe to calculate the pairwise hit probabilities which are written to hit-vectors.txt and the centrality for normalization, written to normalization-distribution.txt
app.calculate_hit_probabilities()
print(odir_tree())
Calculating Hit Probability Vectors...
Calculating Hit Probability Vectors...
PPIN = MINT-human-august2020
SOURCES = proteins-sources-5-entries
TARGETS = proteins-targets-apoptosis-49-entries
r = 0.30 PPIN = MINT-human-august2020
SOURCES = proteins-sources-5-entries
TARGETS = proteins-targets-apoptosis-49-entries
r = 0.01
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-hit-probabilities.exe -i test5s/r0.30/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30 -o test5s/r0.30/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30 | grep Status
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-hit-probabilities.exe -i test5s/r0.01/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01 -o test5s/r0.01/MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01 | grep Status
...Hit Probabilities Calculated.
Source Target Hit Probability
0 O00429 O00220 0.002966
1 O15304 O00220 0.003361
2 P13196 O00220 0.003144
3 P30050 O00220 0.003933
4 P38919 O00220 0.003893
...Hit Probabilities Calculated.
Source Target Hit Probability
0 O00429 O00220 0.001218
1 O15304 O00220 0.003362
2 P13196 O00220 0.001755
3 P30050 O00220 0.011149
4 P38919 O00220 0.015557
Calculating Hit Probability Vectors...
PPIN = MINT-human-august2020
SOURCES = proteins-targets-apoptosis-49-entries
TARGETS = proteins-sources-5-entries
r = 0.01
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-hit-probabilities.exe -i test5s/r0.01/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01 -o test5s/r0.01/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01 | grep Status
Calculating Hit Probability Vectors...
PPIN = MINT-human-august2020
SOURCES = proteins-targets-apoptosis-49-entries
TARGETS = proteins-sources-5-entries
r = 0.30
Running cmd=/home/asq/Dev/inria/projects/sbl/Applications/Genetrank/src/build/sbl-genetrank-hit-probabilities.exe -i test5s/r0.30/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30 -o test5s/r0.30/MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30 | grep Status
...Hit Probabilities Calculated.
Source Target Hit Probability
0 O00429 O00220 0.130106
1 O15304 O00220 0.020702
2 P13196 O00220 0.234095
3 P30050 O00220 0.293829
4 P38919 O00220 0.320440
...Hit Probabilities Calculated.
Source Target Hit Probability
0 O00429 O00220 0.078315
1 O15304 O00220 0.005530
2 P13196 O00220 0.076769
3 P30050 O00220 0.419885
4 P38919 O00220 0.417971
test5s
├── figures
│ └── r0.30
├── r0.01
│ ├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01
│ │ ├── hit-vectors.txt
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_2437.mcl
│ │ ├── mcr_3187.mcl
│ │ ├── mcr_3480.mcl
│ │ ├── mcr_420.mcl
│ │ ├── mcr_679.mcl
│ │ ├── normalization-distribution.txt
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ └── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_10406.mcl
│ ├── mcr_10715.mcl
│ ├── mcr_1560.mcl
│ ├── mcr_2123.mcl
│ ├── mcr_2292.mcl
│ ├── mcr_2743.mcl
│ ├── mcr_2777.mcl
│ ├── mcr_2823.mcl
│ ├── mcr_2995.mcl
│ ├── mcr_3584.mcl
│ ├── mcr_3585.mcl
│ ├── mcr_385.mcl
│ ├── mcr_4131.mcl
│ ├── mcr_4132.mcl
│ ├── mcr_4158.mcl
│ ├── mcr_4407.mcl
│ ├── mcr_4686.mcl
│ ├── mcr_4930.mcl
│ ├── mcr_4932.mcl
│ ├── mcr_5157.mcl
│ ├── mcr_5201.mcl
│ ├── mcr_5251.mcl
│ ├── mcr_5252.mcl
│ ├── mcr_5266.mcl
│ ├── mcr_5296.mcl
│ ├── mcr_5326.mcl
│ ├── mcr_5499.mcl
│ ├── mcr_551.mcl
│ ├── mcr_560.mcl
│ ├── mcr_5668.mcl
│ ├── mcr_5770.mcl
│ ├── mcr_699.mcl
│ ├── mcr_722.mcl
│ ├── mcr_7333.mcl
│ ├── mcr_8055.mcl
│ ├── mcr_8223.mcl
│ ├── mcr_8226.mcl
│ ├── mcr_858.mcl
│ ├── mcr_868.mcl
│ ├── mcr_9210.mcl
│ ├── mcr_9945.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── r0.30
├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_2437.mcl
│ ├── mcr_3187.mcl
│ ├── mcr_3480.mcl
│ ├── mcr_420.mcl
│ ├── mcr_679.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30
├── hit-vectors.txt
├── map_protein_name_idx.txt
├── markov_chain.mcl
├── mcr_10406.mcl
├── mcr_10715.mcl
├── mcr_1560.mcl
├── mcr_2123.mcl
├── mcr_2292.mcl
├── mcr_2743.mcl
├── mcr_2777.mcl
├── mcr_2823.mcl
├── mcr_2995.mcl
├── mcr_3584.mcl
├── mcr_3585.mcl
├── mcr_385.mcl
├── mcr_4131.mcl
├── mcr_4132.mcl
├── mcr_4158.mcl
├── mcr_4407.mcl
├── mcr_4686.mcl
├── mcr_4930.mcl
├── mcr_4932.mcl
├── mcr_5157.mcl
├── mcr_5201.mcl
├── mcr_5251.mcl
├── mcr_5252.mcl
├── mcr_5266.mcl
├── mcr_5296.mcl
├── mcr_5326.mcl
├── mcr_5499.mcl
├── mcr_551.mcl
├── mcr_560.mcl
├── mcr_5668.mcl
├── mcr_5770.mcl
├── mcr_699.mcl
├── mcr_722.mcl
├── mcr_7333.mcl
├── mcr_8055.mcl
├── mcr_8223.mcl
├── mcr_8226.mcl
├── mcr_858.mcl
├── mcr_868.mcl
├── mcr_9210.mcl
├── mcr_9945.mcl
├── normalization-distribution.txt
├── source_idx.txt
├── source_names.txt
└── target_idx.txt
8 directories, 120 files
Scores are calculated by the Genetrank_simulation_result class within SBL_Genetrank_simulation.py using the results from the previous step. Pairwise scores are written to <sources_file_name>_<targets_file_name>_pairwise_scores.csv
app.calculate_scores()
print(odir_tree())
test5s
├── figures
│ └── r0.30
├── r0.01
│ ├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01
│ │ ├── hit-vectors.txt
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_2437.mcl
│ │ ├── mcr_3187.mcl
│ │ ├── mcr_3480.mcl
│ │ ├── mcr_420.mcl
│ │ ├── mcr_679.mcl
│ │ ├── normalization-distribution.txt
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ ├── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01
│ │ ├── hit-vectors.txt
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_10406.mcl
│ │ ├── mcr_10715.mcl
│ │ ├── mcr_1560.mcl
│ │ ├── mcr_2123.mcl
│ │ ├── mcr_2292.mcl
│ │ ├── mcr_2743.mcl
│ │ ├── mcr_2777.mcl
│ │ ├── mcr_2823.mcl
│ │ ├── mcr_2995.mcl
│ │ ├── mcr_3584.mcl
│ │ ├── mcr_3585.mcl
│ │ ├── mcr_385.mcl
│ │ ├── mcr_4131.mcl
│ │ ├── mcr_4132.mcl
│ │ ├── mcr_4158.mcl
│ │ ├── mcr_4407.mcl
│ │ ├── mcr_4686.mcl
│ │ ├── mcr_4930.mcl
│ │ ├── mcr_4932.mcl
│ │ ├── mcr_5157.mcl
│ │ ├── mcr_5201.mcl
│ │ ├── mcr_5251.mcl
│ │ ├── mcr_5252.mcl
│ │ ├── mcr_5266.mcl
│ │ ├── mcr_5296.mcl
│ │ ├── mcr_5326.mcl
│ │ ├── mcr_5499.mcl
│ │ ├── mcr_551.mcl
│ │ ├── mcr_560.mcl
│ │ ├── mcr_5668.mcl
│ │ ├── mcr_5770.mcl
│ │ ├── mcr_699.mcl
│ │ ├── mcr_722.mcl
│ │ ├── mcr_7333.mcl
│ │ ├── mcr_8055.mcl
│ │ ├── mcr_8223.mcl
│ │ ├── mcr_8226.mcl
│ │ ├── mcr_858.mcl
│ │ ├── mcr_868.mcl
│ │ ├── mcr_9210.mcl
│ │ ├── mcr_9945.mcl
│ │ ├── normalization-distribution.txt
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ └── proteins-sources-5-entries_proteins-targets-apoptosis-49-entries-pairwise_scores.csv
└── r0.30
├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_2437.mcl
│ ├── mcr_3187.mcl
│ ├── mcr_3480.mcl
│ ├── mcr_420.mcl
│ ├── mcr_679.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
├── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_10406.mcl
│ ├── mcr_10715.mcl
│ ├── mcr_1560.mcl
│ ├── mcr_2123.mcl
│ ├── mcr_2292.mcl
│ ├── mcr_2743.mcl
│ ├── mcr_2777.mcl
│ ├── mcr_2823.mcl
│ ├── mcr_2995.mcl
│ ├── mcr_3584.mcl
│ ├── mcr_3585.mcl
│ ├── mcr_385.mcl
│ ├── mcr_4131.mcl
│ ├── mcr_4132.mcl
│ ├── mcr_4158.mcl
│ ├── mcr_4407.mcl
│ ├── mcr_4686.mcl
│ ├── mcr_4930.mcl
│ ├── mcr_4932.mcl
│ ├── mcr_5157.mcl
│ ├── mcr_5201.mcl
│ ├── mcr_5251.mcl
│ ├── mcr_5252.mcl
│ ├── mcr_5266.mcl
│ ├── mcr_5296.mcl
│ ├── mcr_5326.mcl
│ ├── mcr_5499.mcl
│ ├── mcr_551.mcl
│ ├── mcr_560.mcl
│ ├── mcr_5668.mcl
│ ├── mcr_5770.mcl
│ ├── mcr_699.mcl
│ ├── mcr_722.mcl
│ ├── mcr_7333.mcl
│ ├── mcr_8055.mcl
│ ├── mcr_8223.mcl
│ ├── mcr_8226.mcl
│ ├── mcr_858.mcl
│ ├── mcr_868.mcl
│ ├── mcr_9210.mcl
│ ├── mcr_9945.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── proteins-sources-5-entries_proteins-targets-apoptosis-49-entries-pairwise_scores.csv
8 directories, 122 files
from SBL import SBL_Genetrank_simulation_statistics
from SBL_Genetrank_simulation_statistics import Genetrank_simulation_visualizations
r03_simulation = app.get_simulation(ppin_file_path, sources_file_path, targets_file_path, pathways_dir_path, 0.3)
r03_simulation_visualizations = Genetrank_simulation_visualizations(r03_simulation)
r03_simulation_visualizations.generate_gene_score_radar('SIVA1', show=True)
app.logFC_logCPM_file = 'data/CellFate-LogCPM-LogFC-pval-FDR-mmc4.xls'
app.generate_gene_score_radar_scatter_plots()
print(odir_tree())
findfont: Font family ['normal'] not found. Falling back to DejaVu Sans. findfont: Font family ['normal'] not found. Falling back to DejaVu Sans. findfont: Font family ['normal'] not found. Falling back to DejaVu Sans. findfont: Font family ['normal'] not found. Falling back to DejaVu Sans. findfont: Font family ['normal'] not found. Falling back to DejaVu Sans.
test5s
├── figures
│ ├── r0.01
│ │ └── score_radar_scatter.pdf
│ └── r0.30
│ └── score_radar_scatter.pdf
├── r0.01
│ ├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.01
│ │ ├── hit-vectors.txt
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_2437.mcl
│ │ ├── mcr_3187.mcl
│ │ ├── mcr_3480.mcl
│ │ ├── mcr_420.mcl
│ │ ├── mcr_679.mcl
│ │ ├── normalization-distribution.txt
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ ├── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.01
│ │ ├── hit-vectors.txt
│ │ ├── map_protein_name_idx.txt
│ │ ├── markov_chain.mcl
│ │ ├── mcr_10406.mcl
│ │ ├── mcr_10715.mcl
│ │ ├── mcr_1560.mcl
│ │ ├── mcr_2123.mcl
│ │ ├── mcr_2292.mcl
│ │ ├── mcr_2743.mcl
│ │ ├── mcr_2777.mcl
│ │ ├── mcr_2823.mcl
│ │ ├── mcr_2995.mcl
│ │ ├── mcr_3584.mcl
│ │ ├── mcr_3585.mcl
│ │ ├── mcr_385.mcl
│ │ ├── mcr_4131.mcl
│ │ ├── mcr_4132.mcl
│ │ ├── mcr_4158.mcl
│ │ ├── mcr_4407.mcl
│ │ ├── mcr_4686.mcl
│ │ ├── mcr_4930.mcl
│ │ ├── mcr_4932.mcl
│ │ ├── mcr_5157.mcl
│ │ ├── mcr_5201.mcl
│ │ ├── mcr_5251.mcl
│ │ ├── mcr_5252.mcl
│ │ ├── mcr_5266.mcl
│ │ ├── mcr_5296.mcl
│ │ ├── mcr_5326.mcl
│ │ ├── mcr_5499.mcl
│ │ ├── mcr_551.mcl
│ │ ├── mcr_560.mcl
│ │ ├── mcr_5668.mcl
│ │ ├── mcr_5770.mcl
│ │ ├── mcr_699.mcl
│ │ ├── mcr_722.mcl
│ │ ├── mcr_7333.mcl
│ │ ├── mcr_8055.mcl
│ │ ├── mcr_8223.mcl
│ │ ├── mcr_8226.mcl
│ │ ├── mcr_858.mcl
│ │ ├── mcr_868.mcl
│ │ ├── mcr_9210.mcl
│ │ ├── mcr_9945.mcl
│ │ ├── normalization-distribution.txt
│ │ ├── source_idx.txt
│ │ ├── source_names.txt
│ │ └── target_idx.txt
│ └── proteins-sources-5-entries_proteins-targets-apoptosis-49-entries-pairwise_scores.csv
└── r0.30
├── MINT-human-august2020_proteins-sources-5-entries_proteins-targets-apoptosis-49-entries_r0.30
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_2437.mcl
│ ├── mcr_3187.mcl
│ ├── mcr_3480.mcl
│ ├── mcr_420.mcl
│ ├── mcr_679.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
├── MINT-human-august2020_proteins-targets-apoptosis-49-entries_proteins-sources-5-entries_r0.30
│ ├── hit-vectors.txt
│ ├── map_protein_name_idx.txt
│ ├── markov_chain.mcl
│ ├── mcr_10406.mcl
│ ├── mcr_10715.mcl
│ ├── mcr_1560.mcl
│ ├── mcr_2123.mcl
│ ├── mcr_2292.mcl
│ ├── mcr_2743.mcl
│ ├── mcr_2777.mcl
│ ├── mcr_2823.mcl
│ ├── mcr_2995.mcl
│ ├── mcr_3584.mcl
│ ├── mcr_3585.mcl
│ ├── mcr_385.mcl
│ ├── mcr_4131.mcl
│ ├── mcr_4132.mcl
│ ├── mcr_4158.mcl
│ ├── mcr_4407.mcl
│ ├── mcr_4686.mcl
│ ├── mcr_4930.mcl
│ ├── mcr_4932.mcl
│ ├── mcr_5157.mcl
│ ├── mcr_5201.mcl
│ ├── mcr_5251.mcl
│ ├── mcr_5252.mcl
│ ├── mcr_5266.mcl
│ ├── mcr_5296.mcl
│ ├── mcr_5326.mcl
│ ├── mcr_5499.mcl
│ ├── mcr_551.mcl
│ ├── mcr_560.mcl
│ ├── mcr_5668.mcl
│ ├── mcr_5770.mcl
│ ├── mcr_699.mcl
│ ├── mcr_722.mcl
│ ├── mcr_7333.mcl
│ ├── mcr_8055.mcl
│ ├── mcr_8223.mcl
│ ├── mcr_8226.mcl
│ ├── mcr_858.mcl
│ ├── mcr_868.mcl
│ ├── mcr_9210.mcl
│ ├── mcr_9945.mcl
│ ├── normalization-distribution.txt
│ ├── source_idx.txt
│ ├── source_names.txt
│ └── target_idx.txt
└── proteins-sources-5-entries_proteins-targets-apoptosis-49-entries-pairwise_scores.csv
9 directories, 124 files
Unless stated otherwise, packages of the SBL are distributed under the following specific license SBL license.
The 