Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Frechet_mean_S1

Authors: F. Cazals and T. O'Donnell

Introduction

Centers of mass and their generalization.

The celebrated center of mass of a point set in a Euclidean space is the (a) point minimizing the sum of squared Euclidean to points in this set.

Similarly, the 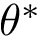$\text{Fr\'echet}$ mean (resp. p-mean) of a point set is a metric space is the point minimizing the sum of squared distances (resp. p-th powers of distances) to a finite point set.

This package provides a method to compute these quantities for points located on the unit circle 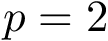$S^1$, following the algorithm from [50] .

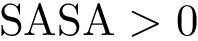
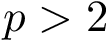
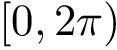
Definitions. Consider $n$ angles $ \Theta_0 = { \theta_1,\dots, \theta_n }$. Also consider the embedding on an angle onto the unit circle, that is $X(\theta)=\transpose{(\cos\theta,\sin\theta)}$.

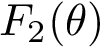
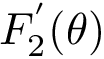
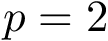
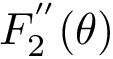
The geodesic distance between the two points $X(\theta)$ and $X(\theta_i)$ on $S^1$, denoted $d(\cdot,\cdot)$, satisfies

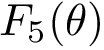
\begin{equation}d(X(\theta), X(\theta_i)) = 2 \arcsin\frac{\vvnorm{X(\theta)-X(\theta_i}}{2}. \end{equation}

This distance is also directly expressed using the angles:

\[d(X(\theta), X(\theta_i)) = \min( \fabs{\theta-\theta_i}, 2\pi - \fabs{\theta-\theta_i}). \]

For an integer 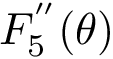$p\geq 1$, consider the function involving the p-th powers of distances to all points, that is

\[\label{eq:Fp} F_p(\theta) = \sum_{i=1,\dots,n} f_i(\theta), \text{ with } f_i(\theta)=d^p(X(\theta), X(\theta_i)). \]

Consider the minimum of this function, that is

\[\label{eq:Fp-min} \theta^* = \arg\min_{\theta\in[0,2\pi)} F_p(\theta). \]

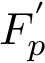
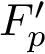
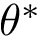
The value $\theta^*$ obtained for $p=2$, corresponds to the $\text{Fr\'echet}$ mean. For $p>2$, the minimum is the so-called p-mean.

Illustrations.

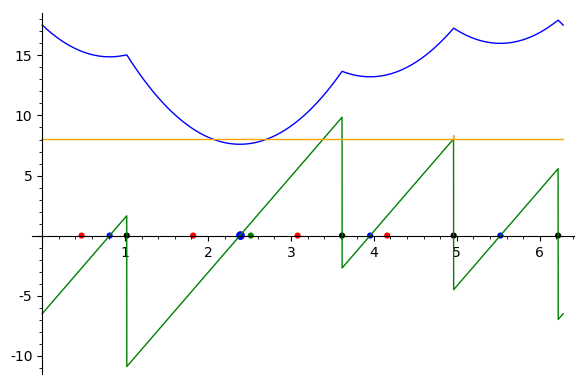Sum of square distances function

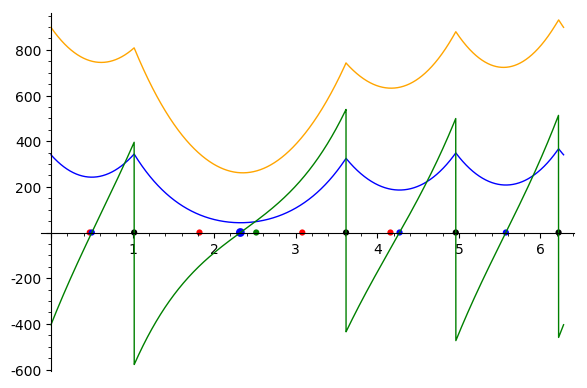Sample points are in red, their antipodal points on the $[0,2\pi)$ circle are in black, minimas are in blue and the larger blue dot is the global minima. In blue $F_2(\theta)$, In green $F^{'}_2(\theta)$ and in yellow $F^{''}_2(\theta)$.

Sum of distances to the power 5 function
Sample points are in red, their antipodal points on the $[0,2\pi)$ circle are in black, minimas are in blue and the larger blue dot is the global minima. In blue $F_5(\theta)$, In green $F^{'}_5(\theta)$ and in yellow $F^{''}_5(\theta)$.

Algorithm

In short, the algorithm [50] subdivides the unit circle into interval namely circle arcs defined by data points and their antipodal values. This set of angles is denoted $\Theta$. These intervals are such that there is at most one local minimum of $F_p$ on each interval. To spot these local minima efficiently, the algorithm maintains a polynomial expression of the function $F_p$ and its derivative $F^{'}_p$. In short, the steps are:

  • Construct the set $\Theta$
  • Sorting angles in $\Theta$
  • For all intervals in I:
  • Identifying the intervals where $F'_p$ vanishes
  • Computing the unique root of $F'_p$ on such intervals
  • Evaluating $F_p$ at local minima, to maintain the global minimum
  • Maintaining the polynomials $F_p$ and $F'_p$ at angles in $\Theta$

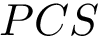
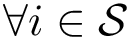
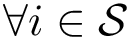
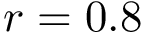
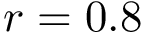
Albeit simple, the algorithm is numerically challenging since it deals with piecewise polynomials with transcendental coefficients (involving $\pi$).

Implementation

Following the classical design pattern in computational geometry, this package provides a generic implementation, templated by a kernel providing number types and associated predicates and constructions.

The main class is SBL::GT::T_Frechet_mean_S1.

Two kernels are provided:

  • SBL::GT::Inexact_predicates_kernel_for_frechet_mean: naive kernel using floating point representations. Therefore, no guarantee on predicates and constructions.
  • SBL::GT::Lazy_exact_predicates_kernel _for_frechet_mean: kernel using a representation of angles and functions $F_p, F_p^{'}$ using interval arithmetic. This representation guarantees exact predicates.

Note that in our case, an erroneous evaluation of predicates may yield the loss or erroneous identification of a local minimum.

Executables

This package provides two executables:

  • sbl-Frechet-mean-using-exact-predicates
  • sbl-Frechet-mean-using-inexact-predicates

This corresponds to the two above mentionned kernels.

Jupyter demo

See the following jupyter notebook:

  • Jupyter notebook file
  • centroid-circle
    In [34]:
    import re  #regular expressions
import sys #misc system
import os
import shutil
#import shutil # python 3 only

#input filename  and output directory
odir = "results"
if not os.path.exists(odir):    
    os.system("mkdir results")
#choose value of p
p=4
angles_file="data/angles.txt" #file containing angles
weights_file="data/weights.txt" #file containing weights
exe_file="sbl-Frechet-mean-using-real-value-NT.exe" #App to compute minimas (sbl-Frechet-mean-using-interval-NT.exe is another option)

# run command(-r is used for specifiying radii input data -a to get all minimas)
cmd = "./%s -f %s -w %s -r -p %d -a -o %s" % (exe_file,angles_file,weights_file,p,odir)
os.system(cmd)
    Out[34]:
    0
    In [35]:
    # load visualisation script and instanciate using data and corresponding minimas
minimas_file="results/angles_local_minima.txt"
load("centroid-circle.sage")
algo = Project()
algo.load_angles(angles_file,False)
algo.load_weights(weights_file)
algo.load_minimas(minimas_file,False)
algo.run(p)

    [1.11764, 4.06681, 5.02666, 4.5149, 0.483089, 4.84806, 6.04743, 0.819754, 1.1358, 4.96215, 5.69144, 0.0488152, 5.8986, 1.04386, 6.1123, 5.30732, 0.492397, 1.57468, 2.25474, 1.01543, 1.08929, 4.58526, 0.147255, 5.77245, 0.00841053, 5.79457, 5.29714, 4.62587, 5.73067, 0.812386]
[1.11764, 4.06681, 5.02666, 4.5149, 0.483089, 4.84806, 6.04743, 0.819754, 1.1358, 4.96215, 5.69144, 0.0488152, 5.8986, 1.04386, 6.1123, 5.30732, 0.492397, 1.57468, 2.25474, 1.01543, 1.08929, 4.58526, 0.147255, 5.77245, 0.00841053, 5.79457, 5.29714, 4.62587, 5.73067, 0.812386]
[1.11764, 4.06681, 5.02666, 4.5149, 0.483089, 4.84806, 6.04743, 0.819754, 1.1358, 4.96215, 5.69144, 0.0488152, 5.8986, 1.04386, 6.1123, 5.30732, 0.492397, 1.57468, 2.25474, 1.01543, 1.08929, 4.58526, 0.147255, 5.77245, 0.00841053, 5.79457, 5.29714, 4.62587, 5.73067, 0.812386]

== Std dev angle from resultant: angle:350.956005808192 var:1.11094971447841


== Running with: num points: 8 exponent: 4
('Angle defining the Frechet mean:', 6.17846555205993, 354.000000000000)
('std dev angle from geo:', 354.000000000000, 1.11137569356359)

    here

    done with formal expressions
[1.14926234641021, 1.40848734641021, 1.46397234641021, 1.59537234641021, 1.76351234641021, 1.85281234641021, 2.02030734641021, 2.16063734641021, 2.35778734641021, 2.56946234641021, 2.60996734641021, 2.64191734641021, 2.70499234641021, 2.83142234641021, 2.93827234641021, 3.06035526500000, 3.17020551858979, 3.23962775358979, 3.45676465358979, 3.62933565358979, 3.79398415358979, 3.95766265358979, 4.05918465358979, 4.17123765358979, 4.20816765358979, 4.24505765358979, 4.26831265358979, 4.49683265358979, 5.05630265358979, 0.0383646928204140]
    In [36]:
    #change value of p
p=5
# rerun command(-r is used for specifiying radii input data)
cmd = "./%s -f %s -w %s -r -p %d -a -o %s" % (exe_file,angles_file,weights_file,p,odir)
algo.run(p)

    == Std dev angle from resultant: angle:350.956005808192 var:1.11094971447841


== Running with: num points: 8 exponent: 5
('Angle defining the Frechet mean:', 6.19591884457987, 355.000000000000)
('std dev angle from geo:', 355.000000000000, 1.11206960096516)

    here

    done with formal expressions
[1.14926234641021, 1.40848734641021, 1.46397234641021, 1.59537234641021, 1.76351234641021, 1.85281234641021, 2.02030734641021, 2.16063734641021, 2.35778734641021, 2.56946234641021, 2.60996734641021, 2.64191734641021, 2.70499234641021, 2.83142234641021, 2.93827234641021, 3.06035526500000, 3.17020551858979, 3.23962775358979, 3.45676465358979, 3.62933565358979, 3.79398415358979, 3.95766265358979, 4.05918465358979, 4.17123765358979, 4.20816765358979, 4.24505765358979, 4.26831265358979, 4.49683265358979, 5.05630265358979, 0.0383646928204140]