 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: R. Tetley and F. Cazals and D. Mazauric
While clustering is ubiquitous in data science, with selected methods provided in the package Cluster_engines, picking a particular clustering algorithm and tuning its parameters is in general a non trivial task.
In order to alleviate this task, this package provides methods to compare two clusterings, by computing a mapping between the clusters of these clusterings. In doing so, groups of clusters called meta-clusters are formed within each clustering, and a 1-to-1 correspondence between these meta-clusters is provided. (We note in passing that our mapping goes beyond a 1-to-1 matching between the clusters [126], [75] .)
The following comments are in order:
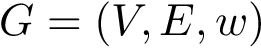
In the sequel, we formalize the clustering comparison problem in a manner answering the two needs just discussed, and document the classes provided. For comparison purposes, this package also provides an implementation of the variation of information (VI) [137] , a metric based on information theoretical concepts.
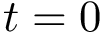
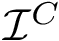
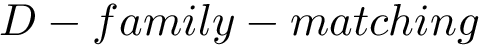
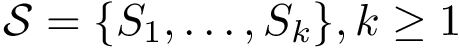
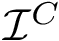
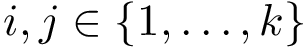
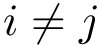
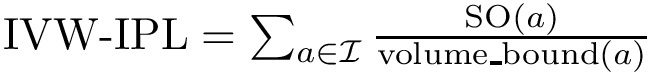
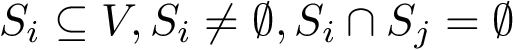
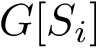
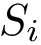
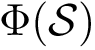
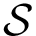
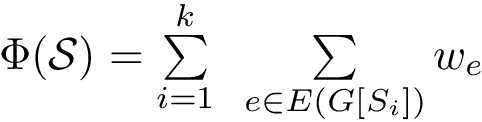
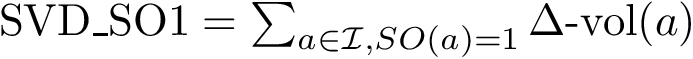
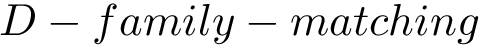
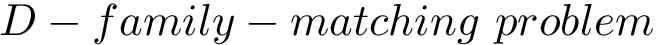
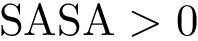
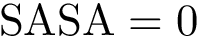
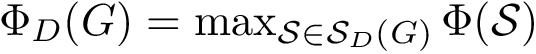
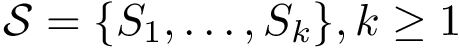
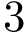
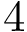
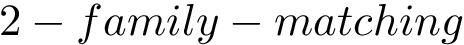
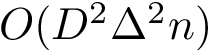
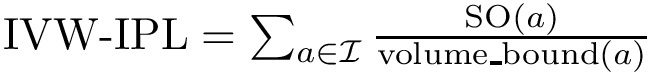

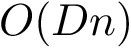
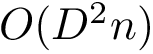

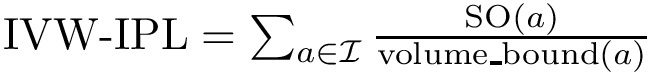
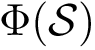
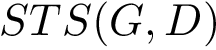
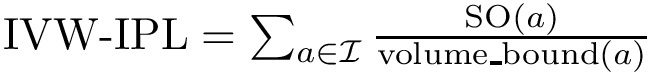
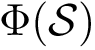
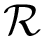
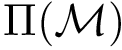
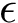
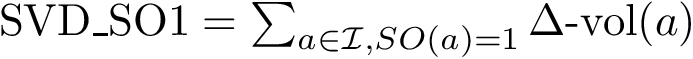
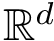
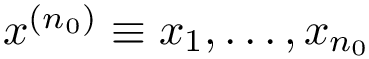
![$G[S_{i}]$](form_300.png)
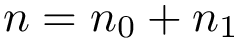
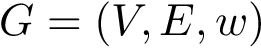
The score 
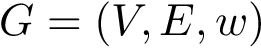
![$\scoreDFM{\mathcal{S}} = \sum\limits_{i=1}^{k}~ \sum\limits_{e \in E(G[S_{i}])} w_{e}$](form_304.png)
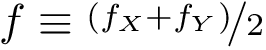
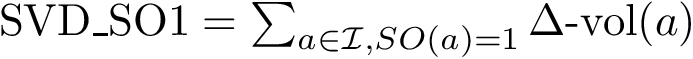
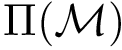
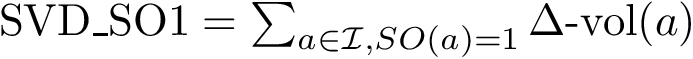
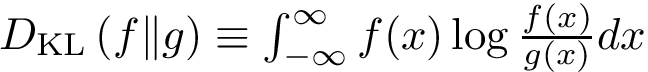
Intuitively, the D-family-matching problem involves computing disjoint subset of nodes (clusters of clusters, or meta-clusters) such that the inconsitencies are minimized (clusters which are in the same meta-cluster have a minimum number of divergent points).
The decision version of the 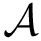
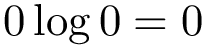
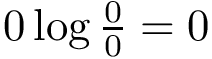
The 
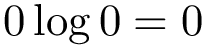
There exist polynomial time algorithms for certain classes of graphs. Denoting 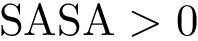
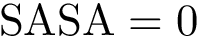
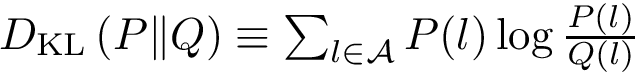
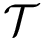
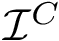
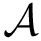
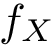
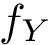
The implemented algorithms follows the generic design presented in [49] .
![\begin{algorithm}\begin{algorithmic}[1]
\Require{An intersection graph $G = (V,E,w)$, an integer $D \geq 1$, a property $\Pi$, a spanning tree generator $\mathcal{R}$, and an algorithm~$\mathcal{A}$.}
\State $\mathcal{M} := \emptyset$, $\lambda := 0$
\While{$\neg~\Pi(\mathcal{M})$}
\State $\lambda : = \lambda + 1$; Compute the spanning tree $T^{\lambda} := \mathcal{R}(G,\lambda)$
\State Compute $\mathcal{S}^{\lambda}$ by using Algorithm~$\mathcal{A}(G,T^{\lambda},D)$; $\mathcal{M} := \mathcal{M} \cup \mathcal{S}^{\lambda}$
\EndWhile
\Return $\mathcal{S} \in \mathcal{M}$ of maximum score
\end{algorithmic}
\caption{Generic algorithm for the $D$-\FM~problem.}
\end{algorithm}](form_316.png)
We implemented a version of the previous algorithm called 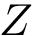
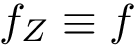
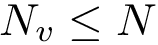
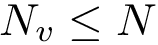
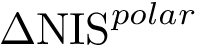
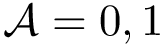
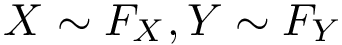
The package is centered around the generic the algorithm discussed above.
This example loads two input clusterings and computes their 3-family matching using random spanning trees or a minimum spanning tree.
This package provides two executables to compare clusterings:
Main options. The main options are:
Input. The two input clusterings. Format specified in the package Cluster_engines .
Main output.
Consists of three files:
See the following jupyter notebook:
from SBL import sbl_jupyter as sblj
help(sblj)
We provide a simple example using the executable sbl-cmp-clust-dfam.exe.
The main options of the cmpClusters in the next cell are:
import re #regular expressions
import sys #misc system
import os
import pdb
import shutil # python 3 only
import matplotlib.pyplot as plt
import matplotlib.image as mplimg
def cmp_clusters(cluster1, cluster2, method = "dfam"):
odir = "results-toy-%s" % method
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
# check executable exists and is visible
exe = shutil.which("sbl-cmp-clust-%s.exe" % method)
if exe:
print(("Using executable %s\n" % exe))
cmd = "sbl-cmp-clust-%s.exe -f %s -f %s -d %s --log" % (method, cluster1, cluster2,odir)
print(cmd)
os.system(cmd)
cmd = "ls %s/*" % odir
ofiles = os.popen(cmd).readlines()
print("All output files:",ofiles)
# we also generate the graph connecting clusters withig meta-clusters, see graph below
if(method=="dfam"):
cmd = "dot -Tpdf %s/sbl-d-family-matching__graph.dot -o %s/graph.pdf" % (odir,odir)
os.system(cmd)
sblj.tools.convert_pdf_to_png( ("%s/graph.pdf" % odir), 150 )
img=mplimg.imread( ("%s/graph.png" % odir) )
plt.xticks([]); plt.yticks([])
imgplot = plt.imshow(img)
#find the log file and display log file
#log = open( ("%s/log.txt") % odir).readlines()
#for line in log: print(line.rstrip())
else:
print("Executable not found")
print("Marker : Calculation Started")
#cmp_clusters("data/cluster_1.txt","data/cluster_2.txt", "VI")
cmp_clusters("data/cluster_1.txt","data/cluster_2.txt")
print("Marker : Calculation Ended")
In the following, we use sbl-cmp-clust-dfam.exe to compare clusterings produced by kmeans. See the package Clustering_engines for the clustering algorithms.
import os
import pdb
import sys
from SBL import PALSE
from PALSE import *
#cluster the input data (contained in the .txt file) set into 5 cluster using k-means++
points_files = ["data/points-N200-d50.txt", "data/points-N200-d50.txt"]
k_values = [10, 20]
def run_with_diameter_constraint(D_max):
odir = "results-%s" % D_max
if os.path.exists(odir):
os.system("rm -rf %s" % odir)
os.system( ("mkdir %s" % odir) )
# Step 1: prepare the individual clusterings of the datasets
clusters_files = [] # files containing cluters
centers_files = [] # files containing cluster centers
for i in range(0, len(points_files)):
cmd = "sbl-cluster-k-means-euclid.exe --k-means-selector=plusplus\
--points-file %s --k-means-k %d -o -d %s" % (points_files[i], k_values[i], odir)
print("Executing ",cmd)
os.system(cmd)
cmd = "find %s -name \"*k_%s__clusters.txt\"" % (odir, k_values[i])
clusters_files.append( os.popen(cmd).readlines()[0].rstrip() )
cmd = "find %s -name \"*k_%s__centers.txt\"" % (odir, k_values[i])
centers_files.append( os.popen(cmd).readlines()[0].rstrip() )
# Step 1b: plot clusterings and collect the images
for i in range(0, len(points_files)):
cmd = "sbl-clusters-display.py -f %s -c %s -C %s -o %s" % (points_files[i], clusters_files[i], centers_files[i], odir)
os.system(cmd)
# collect the plots
cmd = "find %s -name \"*centers.png\"" % odir
lines = os.popen(cmd).readlines()
images = [line.rstrip() for line in lines]
# Step 2: compute the D-family matchig with the constraint D_max given
# Nb: we use 100 iterations by default.
cmd = "sbl-cmp-clust-dfam.exe -f %s -f %s --diameter-constraint %d --num-iterations 100 -d %s" % (clusters_files[0], clusters_files[1], D_max, odir)
print("Clustering comparison command:",cmd)
os.system(cmd)
# Step 3: create a clustering file from the meta-cluster mapping and the original cluster file
cmd = "find %s -name \"*clust1_meta_clusters.txt\"" % odir
meta_cluster_file = os.popen(cmd).readlines()[0].rstrip()
#print(meta_cluster_file)
cmd = "sbl-map-meta-clusters.py -c %s -m %s -o %s/final-clustering.txt" % (clusters_files[0], meta_cluster_file,odir)
os.system(cmd)
cmd = "sbl-clusters-display.py -f %s -c %s/final-clustering.txt -o %s" % (points_files[0],odir,odir)
print("Cluster display command for meta clustering:",cmd)
os.system(cmd)
# Step 4: display all results
cmd = "find %s -name \"*final-clustering.png\"" % odir
final_png = os.popen(cmd).readlines()[0].rstrip()
images.append(final_png)
sblj.tools.show_row_n_images(images, 50)
# Step 5 : palse
database = PALSE_xml_DB()
database.load_from_directory(odir, ".*family_matching")
# total score
score = database.get_all_data_values_from_database("d_family_matching/solution/best_solution/score", int)[0][0]
# stats on meta-clusters
meta_cluster_sizes = database.get_all_data_values_from_database("d_family_matching/solution/best_solution/meta_cluster_sizes/item", int)[0]
print("Score of the matching:",score)
print("Num meta clusters:", len(meta_cluster_sizes))
print("Num of clusters in each meta-clusters:",meta_cluster_sizes)
return odir
In particular, we analyze the incidence of the maximum diameter constraint. Given that the original input file contains 1000 points, note that the total score (num. of points found in meta-clusters) converges rapidly to the maximum possible balue when increasing D_max.
NB: caption for figures:
run_with_diameter_constraint(2)
run_with_diameter_constraint(4)
run_with_diameter_constraint(8)
The reader is referred to [49] for a detailed comparison of VI against the scores yielded by our comparison strategy.