User Manual

Union_find

Authors: F. Cazals and T. Dreyfus

Introduction

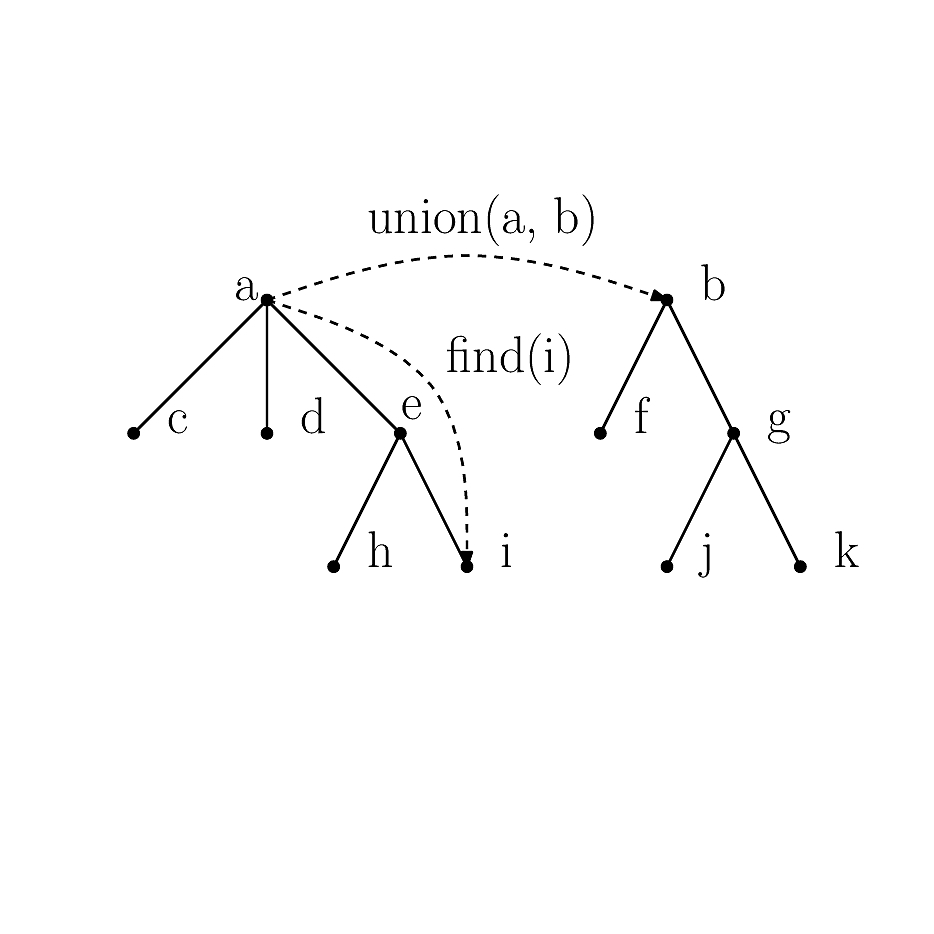
The Union-Find (UF) algorithm maintains dynamically the connected components of an evolving graph, called independent sets in the sequel, upon addition of new edges, thanks to a Union-Find data structure (UF DS). The vertices of this graph may carry a piece of information called the attribute in the sequel.

Union-Find is based on the following three operations:

• make_set: creates a new independent set with one vertex.

• union_sets: merge the independent sets containing two given vertices.

• find_set: returns the independent set of a given vertex.

The key building blocks of the reference UF algorithm are as follows:

• each independent set is represented by a tree whose root is called the leader of the independent set. Each vertex points to its father, the father of the leader being NULL.

• the maintenance of the trees upon addition of new edges uses two strategies known as path-compression and union-by-rank.

Details can be found e.g. in the book Introduction to algorithms, by Cormen-Leiserson-Rivest-Stein [62] .

In addition to the aforementioned basic Union-Find operations, we also provide the following extensions:

• Algorithms: methods to process a list of edges, each of them possibly triggering a union_set operation on the vertices of the edge.

• Leaders: methods to maintain (and iterate on) the list of leaders.

• Independent set iterators: methods to maintain (and iterate on) the independent set containing a given vertex.

• Rewind (aka undo): methods to revert one-by-one a list of operations.

Algorithms

We provide two algorithms to process a list of edges, each of them possibly triggering a union_set operation.

• given a list of edges, iterate over them and calls a union_set on the two vertices of each edge.

• given a predicate, iterate over all edges, and call a union_set on the two vertices of each edge for which the predicate evaluates to True.

An example scenario using these functionalities is given in the SBL::CADS::T_Union_find_specializes section.

Leaders

A linked list of leaders is maintained. (Addition and removal from this list is done in constant time since the vertex data structure actually stores its location in that list.)

Storing the leaders allows :

• retrieving the number of independent sets in constant time,

• iterating over the leaders without considering the other vertices.

Scenarios using this functionality are given in section SBL::CADS::T_Union_find_contains section and SBL::CADS::Union_find_default.

Independent set iterators

Each vertex u is endowed with a linked list of all its children, i.e all the vertices having u as father. (As for leader, each vertex knows it location in that list.)

This extra information allows iterating recursively over all the descendants of a vertex u, i.e all the vertices v for which there is a path in the graph from u to v. In particular, starting from a leader allows visiting its independent set.

Combining this functionality with the iteration on leaders allows visiting the whole Union-Find data structure.

A scenario using this functionality is given in the SBL::CADS::T_Union_find_contains section.

Rewind

Internally, the topology of the UF DS (omitting the maintenance of the ranks) is modified by the following operations:

• MAKE_SET(v) when creating the vertex v

• SET_FATHER(u, v) when setting the father of u to v, during the path compression or union_set operations.

Along a sequence of updates, we stack the aforementioned two operations. To rewind, it is sufficient to unstack these operations, and undo each of them.

A scenario using this functionality is given in section SBL::CADS::T_Union_find_contains.

Implementation

The Union-Find data structure has been designed to handle any attribute type, without sacrificing the efficiency. There are three ways to represent an attribute in the Union-Find data structure:

• The vertex is not associated to any attribute: one can use SBL::CADS::Union_find_default, the default version of the Union-Find data structure implementing a default vertex data structure. See the SBL::CADS::Union_find_default section for an example.

• The vertex contains an attribute of type T : one can use SBL::CADS::T_Union_find_contains < T > implementing a vertex data structure containing the data (accessible with the method data()). Note that if one wishes to issue union_set calls, a mechanism (e.g. a map) mapping an attribute to its vertex is required. The class SBL::CADS::T_Union_find_contains_with_map < T , LessT > has a built-in map allowing to use the Union-Find algorithms as if the data were the vertices. The LessT parameter is a less comparator between objects of type T (default one is std::less< T >). See the SBL::CADS::T_Union_find_contains and SBL::CADS::T_Union_find_contains_with_map sections for an example.

• The vertex inherits from an attribute of type T : one can use SBL::CADS::T_Union_find_specializes < T > implementing a vertex data structure derived from the data type. Note that the previous limitation does not apply. However, inheritance cannot be used for pointer or primitive types (int, float, etc). See the SBL::CADS::T_Union_find_specializes section for an example.

Examples

SBL::CADS::Union_find_default

This example presents the SBL::CADS::Union_find_default class, with a graph encoded in a file. In particular, when the n vertices of the graph are represented by the n first not negative integers , the vertices of the graph can be used as the vertices of the UF DS.

The example reads a graph from a file, and dumps the leaders together with the size of their independent set.

 
#include <SBL/CADS/Union_find.hpp>
#include <iostream>
#include <fstream>
#include <algorithm>
 
 
//No data attached to a UF vertex
typedef SBL::CADS::Union_find_default                                            Union_find;
typedef Union_find::Vertex                                                  Vertex;
typedef std::pair<Vertex*, Vertex*>                                         Edge;
 
int main(int argc, char *argv[])
{
  Union_find UF;
 
  //Read a file containing:
  if(argc < 2) return -1;
  std::ifstream in(argv[1]);
  std::vector<Edge> edges;
  //Store all edges from the file. 
  while(!in.eof()){
    unsigned u, v; 
    in >> u;
    if(in.eof()) continue;
    in >> v;
    if(in.eof()) continue;
    while(UF.get_number_of_vertices() <= std::max(u, v))
      UF.make_set();
    edges.push_back(Edge(UF[u], UF[v]));
  }
 
  in.close();
 
  //Link the vertices using Union-Find algorithm.
  UF.union_from_edges(edges.begin(), edges.end());  
 
  //Print statistics:
  std::cout << "Number of independent sets: " << UF.get_number_of_independent_sets() << std::endl;
  
  std::cout << "Size of independent sets:";
  for(Union_find::Leaders_iterator it = UF.leaders_begin(); it != UF.leaders_end(); it++)
    std::cout << " " << UF.get_size_of_independent_set(*it);
  std::cout << std::endl;
 
  UF.clear();
 
  return 0;
}

SBL::CADS::T_Union_find_contains

This example presents the SBL::CADS::T_Union_find_contains class, using the Rewind functionality. It fills the Union-Find data structure with n vertices representing proteins, makes an arbitrary union of them, rewinds the Union-Find data structure to the last insertion, and re-makes a new arbitrary union of the vertices.

Since we need to attach an attribute to the Union-Find vertices, but we do not need to access a vertex from its associated data, we use the SBL::CADS::T_Union_find_contains class instantiated with the Protein const reference data type. (Note that instantiating directly with the data type will copy the data instead of copying the const reference to the data).

 
#include <SBL/CADS/Union_find.hpp>
#include <iostream>
#include <algorithm>
#include <string>
#include <fstream>
#include <sstream>
 
//Data structure representing a protein
class Protein_base
{
  std::string m_name;
public:
  Protein_base(const std::string& name = "noname"):m_name(name){}
  friend std::ostream& operator<<(std::ostream& out, const Protein_base& P)
  {out << P.m_name; return out;}
};
 
//A UF vertec contains a const reference to a protein.
typedef SBL::CADS::T_Union_find_contains<const Protein_base&> Union_find;
typedef Union_find::Vertex                          Vertex;
 
int main(int argc, char *argv[])
{
  Union_find UF;
 
  //n: number of proteins; 
  unsigned n = 4;
  if(argc > 1)
    n = atoi(argv[1]);
 
  //Create the proteins.
  std::vector<Protein_base> proteins;
  for(unsigned i = 0; i < n; i++){
    std::ostringstream oss; oss << "P" << i;
    proteins.push_back(oss.str());
  }
 
  //Fill the Union-Find structure with the proteins.
  for(unsigned i = 0; i < proteins.size(); i++)
    UF.make_set(proteins[i]);
 
  //Link the first and the last vertices.
  UF.union_sets(UF[0], UF[proteins.size() - 1]);
  std::cout << "Number of protein complexes after first unions: " 
            << UF.get_number_of_independent_sets() << std::endl;
  
  //Rewind the UF structure before the last inserted vertex.
  UF.rewind_to_last_make_set();
  std::cout << "Number of protein complexes after rewind: " 
            << UF.get_number_of_independent_sets() << std::endl;
 
  return 0;
}

SBL::CADS::T_Union_find_contains_with_map

This example presents the SBL::CADS::T_Union_find_contains_with_map class. It uses the last example, but uses directly the data as input of Union-Find methods.

#include <SBL/CADS/Union_find.hpp>
#include <iostream>
#include <algorithm>
#include <string>
#include <fstream>
#include <sstream>
 
//Data structure representing a protein
class Protein_base
{
  std::string m_name;
public:
  Protein_base(const std::string& name = "noname"):m_name(name){}
  friend std::ostream& operator<<(std::ostream& out, const Protein_base& P)
  {out << P.m_name; return out;}
  friend bool operator<(const Protein_base& p_1, const Protein_base& p_2)
  {return p_1.m_name < p_2.m_name;}
};
 
//A UF vertec contains a const reference to a protein.
typedef SBL::CADS::T_Union_find_contains_with_map<Protein_base*> Union_find;
typedef Union_find::Vertex                          Vertex;
 
int main(int argc, char *argv[])
{
  Union_find UF;
 
  //n: number of proteins; 
  unsigned n = 4;
  if(argc > 1)
    n = atoi(argv[1]);
 
  //Create the proteins.
  std::vector<Protein_base*> proteins;
  for(unsigned i = 0; i < n; i++){
    std::ostringstream oss; oss << "P" << i;
    proteins.push_back(new Protein_base(oss.str()));
  }
 
  //Fill the Union-Find structure with the proteins.
  for(unsigned i = 0; i < proteins.size(); i++)
    UF.make_set(proteins[i]);
 
  //Link the the first and the last vertices.
  UF.union_sets(proteins.front(), proteins.back());
  std::cout << "Number of protein complexes after first unions: " 
            << UF.get_number_of_independent_sets() << std::endl;
 
  //Rewind the UF structure before the last inserted vertex.
  UF.rewind_to_last_make_set();
  std::cout << "Number of protein complexes after rewind: " 
            << UF.get_number_of_independent_sets() << std::endl;
 
  for(unsigned i = 0; i < n; i++)
    delete proteins[i];
  return 0;
}

SBL::CADS::T_Union_find_specializes

This example presents the the SBL::CADS::T_Union_find_specializes class.

Consider a set of proteins with a set of known contacts between them. First, we use the Union-Find data structure for maintaining the independent sets of proteins upon processing the contacts. We then check whether two specific proteins belong to the same independent set.

We use the SBL::CADS::T_Union_find_specializes class instantiated with the Protein_base data type. In doing so, the SBL::CADS::T_Union_find_vertex_data_structure_specializes type directly represents the data.

Note that we need to create new instances of the base data types, but we cast the pointers to the base data type to pointers to the vertex type: this way, the data are not copied.

#include <iostream>
#include <fstream>
#include <sstream>
#include <stdlib.h> 
#include <algorithm> 
 
#include <SBL/CADS/Union_find.hpp>
 
//Base data structure representing a protein
class Protein_base
{
  std::string m_name;
public:
  Protein_base(const std::string& name = "noname"):m_name(name) {}
  void set_name(const std::string& name){this->m_name = name;}
  friend std::ostream& operator<<(std::ostream& out, const Protein_base* P)
  {out << P->m_name; return out;}
};
 
//The vertex data structure inherits from Protein_base
typedef SBL::CADS::T_Union_find_specializes<Protein_base>  Union_find;
typedef Union_find::Vertex                            Protein;
 
void delete_protein(Protein* p){delete p;}
 
int main(int argc, char *argv[])
{
  // Destruction of UF (Union_find object) cannot occur properly if the proteins have been destroyed beforehand, since its destruction require vertices (Proteins in the current case) to be initialized.
  // To ensure proper clearing of the memory, the Union_find is instanciated on the heap to control its destruction (scoping could have held similar results)
  Union_find* UF = new Union_find();
 
  //n: number of proteins; 
  unsigned n = 10;
  if(argc > 1) { n = atoi(argv[1]); }
 
  // Create the n protein instances, and insert them in the UF engine.
  std::vector<Protein*> proteins;
  for (unsigned i = 0; i < n; i++) {
    std::ostringstream oss;
    oss << "P" << i;
    proteins.push_back(new Protein());
    proteins.back()->set_name(oss.str());
    UF->make_set(proteins.back());
  }
 
  //Create the contacts (1 here between the first and the last proteins)
  std::list<std::pair<Protein*, Protein*> > contacts;
  contacts.push_back(std::make_pair(proteins.front(), proteins.back()));
  
  //Link them using Union-Find algorithm.
  UF->union_from_edges(contacts.begin(), contacts.end());
 
  //Check that the first and the last proteins are in the same set.
  std::cout << proteins.front() << " and " << proteins.back();
  if(UF->find_set(proteins.front()) == UF->find_set(proteins.back())) {
    std::cout << " are in same set" << std::endl;
  } else {
    std::cout << " are in different sets" << std::endl;
  }
 
  // deleting UF won't get rid of the Protein objects instanciated on the heap
  delete UF;
 
  // call the desctructor on each protein instance
  std::for_each(proteins.begin(), proteins.end(), delete_protein);
 
  return 0;
}