Nucleic_acid_representation

Authors: F. Cazals and C. Robert

A pivotal X-ray diffraction image (Photo 51) of B-form DNA obtained by Rosalind Franklin and her graduate student in 1952, which permitted Francis Crick and James Watson to decipher the double-helical structure of the macromolecule.

Introduction

Like proteins, nucleic acids consist of linear chains of residues. In RNA and DNA these residues are the ribo- (RNA) or deoxy-ribo- (DNA) nucleotides.

This package focuses on specific SBL functionalities for nucleic acids (NA), and, like the Protein_representation package, depends on the generic linear polymer chain properties from the package Linear_polymer_representation for much of its basic functionality.

The figure below shows the atom names and topology (covalent structure) of a single nucleotide residue in the context of a polynucleotide chain. The detailed structure of the nucleotide pyrimidine (single ring) or purine (double ring) base, both essentially planar, are not shown in the diagram.

Dihedral angles along the backbone of a single nucleotide i in the polynucleotide chain. [nakb.org]

Classes offered. The principle classes provided for nucleic acids are:

Class SBL::CSB::T_Polynucleotide_chain_representation : to access geometric, topological and biochemical information for a single polynucleotide chain.
Class SBL::CSB::T_Nucleic_acid_representation: to access the chains of a Nucleic acid quaternary structure.
Class SBL::IO::T_Nucleic_acid_representation_loader : to create instances of the previous two classes.

Recall that a PDB file may define several geometric models, typically if the structure is determined by NMR. If so, the loader forces the choice of one model. For this model, a SBL::CSB::T_Nucleic_acid_representation containing instances of SBL::CSB::T_Polynucleotide_chain_representation is returned.

Using the Nucleic_acid and Polynucleotide representations

The demo program sbl-na-info.cpp provides examples of using the different functionalities in Nucleic acid and Polynucleotide chain representations in the SBL. Many of these operations are nearly identical to those presented already in the Protein_representation User manual.

The executable for this program can be run in the terminal using the following command to provide an overview of the PDB file 280D:

Rendering of the RNA double helix (chains C-D) in PDB structure 280D.

./sbl-na-info.exe -f 280D.pdb

This PDB entry contains the structures of four RNA chains resolved by X-ray crystallography, for 2 double helices making up the aymmetric unit. The different types of information output by this program are excerpted and discussed briefly in the next few subsections.

After this initial overview, implementation details for Polynucleotide chains will be exposed in more detail in section 3.

Loading nucleic acids and polynucleotide chains

Load a polynucleotide chain from a PDB file and access its different geometrical properties.

For a PDB file containing polynucleotide chains only (i.e., no proteins), a Nucleic acid loader can be invoked directly for that file as shown here. In the case of a PDB file continaing more than one type of component (e.g., proteins and nucleic acids), the more general loader in Biomolecule_representation should be used.

The following code loads the polynucleotide chain(s) from the PDB file specified on the command line.

Nucleic_acid_loader loader;
parse_command_line(argv, argc, loader);
bool b = loader.load(true, std::cout);
 
if(!b)
  return -1;
 
Nucleic_acid_representation& na = *(loader.get_nucleic_acid_representations()[0]);
//

Note that the function parse_command_line has been employed to provide the loader with command-line arguments specifying the path to the pdb file to parse.

As in the example for loading a protein from a PDB file (Protein_representation), loading a nucleic acid produces a short summary of the information obtained, including the number of atoms whose coordinates were read (embedded atoms). Also, as in the protein loader example, if multiple models are present for a single entity in the PDB file– a common case for NMR structures– the lowest index model is chosen.

    Number of loaded PDB files: 1
    Details for each file:
    -- file 1 280D.pdb: 
    -- -- File exists: Yes
    -- -- File is valid: Yes
    -- -- Number of models: 1
    -- -- Number of loaded atoms (of model with lowest index): 1008
    -- -- Number of loaded SS bonds: 0
    -- -- Number of discarded atoms based on model id (all models): 0
    -- -- Number of discarded atoms based on chain id (all models): 0
    -- -- Number of discarded atoms based on b factor beeing too high (all models): 0
    -- -- Number of discarded waters (all models): 158
    -- -- Number of discarded hetatoms (all models): 158
    -- -- Number of discarded hydrogens (all models): 0
    -- -- Number of discarded alternate location atoms (all models): 0
    -- -- Number of actually discarded atoms (all models): 158
    Covalent Structure File Loader statistics:
    -- -- Number of molecular covalent structures: 1
    -- Molecular covalent structure 0:
    -- -- Number of particles: 1512
    -- -- Number of embedded particles: 1008
    -- -- Number of bonds: 1624
    -- -- Number of embedded bonds: 1120
    -- -- Number of disulfide bonds: 0
    Nucleic_acid Representation Loader statistics:
    Number of loaded nucleic_acids: 1
    Details for each nucleic acid :
    -- structure 1:
    -- -- Number of chains: 4
    -- -- Number of residues: 48
    -- -- Number of particles: 1512
    -- -- Number of embedded particles: 1008
    -- -- Number of bonds: 1624
    -- -- Number of embedded bonds: 1120

    Statistics over chain D
    Chain type is RNA
    Found 1 connected component(s) in the chain

     [...]

Each chain in the PDB file is analyzed in turn. Note that the chains are analyzed in the stored "stack" order: last in (chain D) first out (LIFO).

The output indicates that a nucleic acid (NA) chain has been read, and the chain type. This is inferred through the presence of a 1- or 2-character residue name (RNA or DNA, respectively) for the first residue in the PDB file, as opposed to a 3-character amino-acid residue name used to assign the "Protein" type for polypeptide chains.

Details are provided in the section The MCS builder for biomolecules and the switch Protein vs Nucleic Acid. of the package Biomolecule_representation.

Chain composition, residue and atom enumeration.

Accessing information at the residue and atom level of the polynucleotide chain is done just as in the case of the Polypeptide chain, explained in Section Using Polypeptide chain and protein representations of the package Protein_representation.

The atom composition of the polynucleotide chain is distinct from that of polypeptide chains, notably by the presence of phosphorus in phosphate group of each residue of the chain backbone.

    --- Number of atoms of each type :
    -- -- C : 113
    -- -- N : 43
    -- -- O : 85
    -- -- P : 11
    -- -- min / max / average of temperature factors : 13.85 39 26.1742

    -- Calculate number of residues of each type :
    -- -- C : 4
    -- -- G : 5
    -- -- U : 3
    Num residues: 12
    -- -- Found in the backbone between resids 37  and 48 :  P:11 C4':12

Built-in atom iterators are pre-programmed for key backbone atoms. For instance, the atom C4' in Polynucleotide_chain_representation is taken as the branch point for the nucleotide "side chain" in each nucleotide residue.

The coordinates of these (embedded) atoms can be accessed and used for example to calculate their center of mass, as was done for the Polypeptide_chain C_alpha atoms, or for the whole biomolecule.

//Compute the center of mass of the C4'
std::cout << std::endl << "-- Geometric statistics :" << std::endl;
double x = 0, y = 0, z = 0, num_c4ps = 0;
for(Polynucleotide_chain::C4p_iterator it = P.c4ps_begin(); it != P.c4ps_end(); it++)
  {
    x += P.get_x(*it); y += P.get_y(*it); z += P.get_z(*it);
    num_c4ps++;
  }
x /= num_c4ps; y /= num_c4ps; z /= num_c4ps;
Polynucleotide_chain::Point_3 com = P.compute_heavy_atoms_center_of_mass();
std::cout << "-- -- Center of mass of C4' atoms: (" << x << ", " << y << ", " << z << ")" << std::endl;
std::cout << "-- -- Center of mass of Heavy atoms: (" << com.x() << ", " << com.y() << ", " << com.z() << ")" << std::endl;
 
//Translate the protein two angstroms in the x direction
for(Polynucleotide_chain::Atoms_iterator it = P.atoms_begin(); it != P.atoms_end(); it++)
  P.get_x(*it) += 2;
 
Polynucleotide_chain::Point_3 new_com = P.compute_heavy_atoms_center_of_mass();
double distance = CGAL::sqrt(CGAL::squared_distance(com, new_com));
std::cout << "-- -- Distance between new and old center of mass: " << distance << std::endl;

With the expected results:

    -- Geometric statistics :
    -- -- Center of mass of C4' atoms: (0.48075, -7.49417, 2.1645)
    -- -- Center of mass of Heavy atoms: (0.385365, -6.87031, 1.74067)
    -- -- Distance between new and old center of mass: 2

Accessing internal coordinates of the polynucleotide chain.

Bond lengths, angles and dihedral angles can be iterated over using general iterators inherited from Linear_polymer_representation and more generally Molecular_covalent_structure. The following example code simply shows the result of averaging these values over the whole bioùmolecule:

//Compute internal coordinates using iterators over all of them :
double mean_length = 0, num_bonds = 0;
for(Polynucleotide_chain::Bond_iterator it = P.bonds_begin(); it != P.bonds_end(); it++)
  {
    mean_length += (*it).get_bond_length();
    num_bonds++;
  }
std::cout << "-- -- Mean bond length: " << (mean_length/num_bonds) << std::endl;
 
double mean_valence_angle = 0, num_angles = 0;
for(Polynucleotide_chain::Bond_angle_iterator it = P.bond_angles_begin(); it != P.bond_angles_end(); it++)
  {
    mean_valence_angle +=  (*it).get_valence_angle();
    num_angles++;
  }
std::cout << "-- -- Mean valence angle: " << (mean_valence_angle/num_angles) << std::endl;
 
double mean_dihedral_angle = 0;
num_angles = 0;
for(Polynucleotide_chain::Dihedral_angle_iterator it = P.dihedral_angles_begin(); it != P.dihedral_angles_end(); it++)
  {
    mean_dihedral_angle +=  (*it).get_dihedral_angle();
    num_angles++;
  }
std::cout << "-- -- Mean dihedral angle: " << (mean_dihedral_angle/num_angles) << std::endl;

Producing

    -- -- Mean bond length: 1.42829
    -- -- Mean valence angle: 1.98472
    -- -- Mean dihedral angle: -0.0553868

Iterating over backbone dihedral angles by residue.

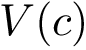
The conformation of a polynucleotide chain backbone is defined by 6 dihedrals ( $\alpha, \beta, ...$ ) for each nucleotide, as opposed to 3 ( $\phi, \psi, \omega$ ) for each amino-acid unit in a polypeptide chain.

Dedicated angle iterators

As is the case for polypeptide chains, a dedicated iterator may be used to calculate a given torsion angle, residue-by-residue, along the chain. For example, the average value of the backbone dihedral angle "alpha" over the entire chain may be calculated using the function get_alpha_angle():

// Calculate mean alpha angle by iterating over residues
double mean_angle;
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Residues_iterator it = P.residues_begin(); it != P.residues_end(); it++)
  {
        Residue& res = *it;
    unsigned resid = res.residue_sequence_number();
    mean_angle += resid != P.get_first_residue().residue_sequence_number() ? P.get_alpha_angle(res).second : 0;
    num_angles += resid != P.get_first_residue().residue_sequence_number() ? 1 : 0;
  }
std::cout << "-- -- Mean alpha angle (using dedicated dihedral angle function): " << to_degrees((mean_angle/num_angles)) << std::endl;

with the result

    -- -- Mean alpha angle (using dedicated backbone dihedral angle function): -67.4058

Chosen-angle iterator for any enumerated angle

On the other hand, it may be more convenient to be able to specify a given dihedral angle using a more programmatic approach. One way to do this in the SBL is through the use of a Chosen_angle_iterator with an enum such as NT_alpha representing the alpha angle (see implementation in the following section).

// Iterate over alpha dihedral angles by using a Chosen_angle_iterator which is a Dihedral_angle_iterator filtered using NT_alpha as chosen_angle
Polynucleotide_chain::Is_Chosen_angle chosen_angle(SBL::CSB::NT_alpha);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
  }
std::cout << "-- -- Mean alpha angle (using Chosen_angle_iterator): should match preceding " << to_degrees((mean_angle/num_angles)) << std::endl;

This syntax declares and instantiates an object chosen_angle that is tailored to the dihedral angle NT_alpha.

Note that this object may be reassigned to a different angle, e.g., NT_beta, using the syntax chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_beta) as shown in the next example.

    -- -- Mean alpha angle (using Chosen_angle_iterator): should match preceding -67.4058

The result is identical, with the advantage is that a single syntax can thus be used to specify any number of dihedral angles.

For instance, in the following code, a simple modification of the enum assigned to "chosen_angle" adapts the iterator to each of the 6 backbone angles in turn. Finally, at the end of this code block, the non-backbone dihedral angle enum NT_pyr (referring to the nucleotide 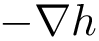$\chi$ angle) allows calculating the orientation of the pyrimidine bases C T or U with respect to the ribose sugar in each residue.

// Iterate over beta dihedrals using a different Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_beta);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
    }
std::cout << "-- -- Mean beta angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;
 
// Iterate over gamma dihedrals using a different Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_gamma);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
    }
std::cout << "-- -- Mean gamma angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;
 
// Iterate over gamma dihedrals using a different Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_delta);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
    }
std::cout << "-- -- Mean delta angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;
 
// Iterate over gamma dihedrals using a different Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_epsilon);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
    }
std::cout << "-- -- Mean epsilon angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;
 
// Iterate over gamma dihedrals using a different Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_zeta);
mean_angle = 0; num_angles = 0;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    mean_angle +=  (*it).get_dihedral_angle();
    num_angles++;
    }
std::cout << "-- -- Mean zeta angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;
 
// Iterate over another defined dihedral using a Chosen_angle_iterator
chosen_angle = Polynucleotide_chain::Is_Chosen_angle(SBL::CSB::NT_pyr);
mean_angle = 0; num_angles = 0;
double angle;
for(Polynucleotide_chain::Chosen_angle_iterator it = P.chosen_angles_begin(chosen_angle); it != P.chosen_angles_end(chosen_angle); it++){
    angle = (*it).get_dihedral_angle();
    std::cout << "  " << to_degrees(angle) << std::endl;
    mean_angle +=  angle;
    num_angles++;
    }
std::cout << "-- -- Mean pyrimidine chi angle (using Chosen_angle_iterator): " << to_degrees((mean_angle/num_angles)) << std::endl;

The output is shown here.

    -- -- Mean beta angle (using Chosen_angle_iterator): -17.4165
    -- -- Mean gamma angle (using Chosen_angle_iterator): 51.3045
    -- -- Mean delta angle (using Chosen_angle_iterator): 82.058
    -- -- Mean epsilon angle (using Chosen_angle_iterator): -154.506
    -- -- Mean zeta angle (using Chosen_angle_iterator): -70.8185
      -153.58
      -158.475
      -166.811
      -159.013
      -144.791
      -160.379
      -143.059
    -- -- Mean base chi angle (using Chosen_angle_iterator): -155.158

Note that the program reports each value of the chi angle as well as the average value.

Iterating over backbone dihedrals within a nucleotide

The program sbl-na-info.exe also shows how to calculate the backbone dihedral angles in sequence for a given nucleotide in the polynucleotide chain.

This demonstration makes use of the general function get_backbone_torsion_angle(), which makes use of the order of backbone atom names in the "backbone trace" for a nucleotide residue, as defined in Polynucleotide_chain_representation.hpp.

std::cout << "Residue " << res.residue_name() << " chain " << P.get_chain_id() << " sequence number is "  << res.residue_sequence_number() << "\n";
...
// Calculate by iterating over backbone dihedral angle names with backbone dihedral angle offset map
std::cout << "==> Iterate over backbone dihedral-angle names to get dihedral angles" << std::endl;
std::string angle_name;
int offset;
for( auto angle_name: P.da_backbone_names){
  offset = P.da_backbone_offset_map.at(angle_name);
  angle = P.get_backbone_torsion_angle(offset, res).first ? to_degrees(P.get_backbone_torsion_angle(offset, res).second) : -999;
  std::cout << angle_name << " (offset " << offset << ") : " << angle << std::endl;
}

In this example, for a given residue object res, the function get_backbone_torsion_angle is called in a loop over a list of backbone dihedral angle names and providing an offset value along the backbone_trace at each iteration. (Details of the calculation are given in the Implementation section below.)

    Residue G chain D sequence number is 37
    Atom-in-residue: 0 757 O5'
    Atom-in-residue: 1 758 C5'
    Atom-in-residue: 2 759 C4'
    Atom-in-residue: 3 760 O4'
    Atom-in-residue: 4 761 C3'
    Atom-in-residue: 5 762 O3'
    Atom-in-residue: 6 763 C2'
    Atom-in-residue: 7 764 O2'
    Atom-in-residue: 8 765 C1'
    Atom-in-residue: 9 766 N9
    Atom-in-residue: 10 767 C8
    Atom-in-residue: 11 768 N7
    Atom-in-residue: 12 769 C5
    Atom-in-residue: 13 770 C6
    Atom-in-residue: 14 771 O6
    Atom-in-residue: 15 772 N1
    Atom-in-residue: 16 773 C2
    Atom-in-residue: 17 774 N2
    Atom-in-residue: 18 775 N3
    Atom-in-residue: 19 776 C4
    angle alpha:-999
      angle beta:-999
    ==> Iterate over backbone dihedral-angle names to get dihedral angles
    NT_alpha (offset -1) : -999
    NT_beta (offset 0) : -999
    NT_gamma (offset 1) : 55.2773
    NT_delta (offset 2) : 84.6034
    NT_epsilon (offset 3) : -148.633
    NT_zeta (offset 4) : -75.0411

In this example, G 37 is the first nucleotide in the polynucleotide chain D. Both the alpha and beta angles are undefined; alpha as it depends on the O3' atom of the (nonexistent) preceding residue, and beta because this crystal structure is also missing the 5' phosphate atom.

Iterating over ribose dihedrals

Finally, we demonstrate a particular use in the polynucleotide chain context of the Ordered_chain_iterator, declared in Linear_polymer_representation.hpp. This iterator is intended for traversing the dihedral angles along a branch (side chain) connected to the main-chain polymer backbone.

Whereas in a polypeptide chain the Ordered_chain_iterator accesses the Chi dihedral angles (Chi_1, Chi_2, ...) for each amino-acid residue, in the polynucleotide chain it accesses the dihedral angles of the ribose ring (Nu_0; Nu_1, ...), while terminating with Nu_0b (a dihedral angle coaxial with Nu_0) and the single Chi dihedral associated with the nucleotide (see Figure in next section).

Unlike the polypeptide chain case, which refers to side-chain angles with a uniform naming convention Chi_1, Chi_2, etc., the angle names for polynucleotides are obtained using a specialized names vector P.da_sidechain_names for convenience.

// Calculate using the standard Chi_iterator using nucleotide-appropriate names (Nu_0, Nu_1, ...)
std::cout << "==> Iterate over side-chain dihedral angles" << std::endl;
Polynucleotide_chain::Chi_iterator itb = P.chi_angles_begin(res), ite = P.chi_angles_end(res);
int j = 0;
for(; itb != ite; itb++){
  angle_name = P.da_sidechain_names[j++];
  std::cout << angle_name << " : " << to_degrees( (*itb).get_dihedral_angle() ) << "\n";
}
std::cout << "\n";

This results in the following output for nucleotide G 37:

    ==> Iterate over side-chain dihedral angles
    Nu_0 : 12.3616
    Nu_1 : -35.5998
    Nu_2 : 44.1901
    Nu_3 : -38.0158
    Nu_4 : 16.2145
    Nu_0b : -105.053
    Chi : 179.877

(It can be noted here that ribose nu_3 is coaxial with the backbone angle delta.)

Again, implementation details are left to the following section.

Implementation and functionality

In this section we survey the specialization of the general Linear-polymer representation to the Polynucleotide chain, with relevant code snippets taken from Polypeptide_chain_representation.hpp

For reference, the figure below shows the nucleotide chemical structure together with the backbone torsion angles, already depicted at the top of this document, as well as the torsions of the ribose ring and around the glycosidic bond 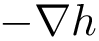$\chi$ .

Backbone and ribose dihedral angles in the polynucleotide chain. [Markley1998, IUPAC document]

Accessing named dihedral angles

Any dihedral angle in the polymer chain can be calculated using the class T_Linear_polymer_representation::Dihedral_angle, which takes 4 embedded atom instances as arguments.

One may decide to access any desired angle by explicitly coding a new dedicated function along the lines of P.get_alpha_angle() shown in the previous section.

However, the polypeptide or polynucleotide chain representation also defines an enumerated set of named dihedral angles of particular interest. For nucleotides, this includes the backbone dihedral angles as well as the 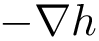$\chi$ angle defining the orientation of the pyrimidine or purine base with respect to the ribose sugar.

In Polynucleotide_chain_representation.hpp the enums for these dihedral angles are placed in the SBL::CSB namespace, using a "NT_" prefix to indicate that they apply to nucleotides.

// Enum and map defining particular dihedral angles in nucleic acids
enum Nucleic_acid_dihedral_angle {NT_alpha, NT_beta, NT_gamma, NT_delta, NT_epsilon, NT_zeta, NT_pyr, NT_pur};
typedef std::map<Nucleic_acid_dihedral_angle, std::tuple<std::string,std::string,std::string,std::string>>  Nucleic_acid_dihedral_angles_map_type;

Each dihedral angle enum is associated with the 4-tuple of atom names used to calculate each angle via a map called the "s_da_map", which is specified in T_Polynucleotide_chain_representation as

//  da_map backbone entries could be added automatically using a (head-to-tail joined) backbone_trace
Base::s_da_map =  {
    {NT_alpha,   std::make_tuple("O3'", "P",   "O5'", "C5'")},  // O3' here is in residue i-1
    {NT_beta,    std::make_tuple("P",   "O5'", "C5'", "C4'")},
    {NT_gamma,   std::make_tuple("O5'", "C5'", "C4'", "C3'")},
    {NT_delta,   std::make_tuple("C5'", "C4'", "C3'", "O3'")},
    {NT_epsilon, std::make_tuple("C4'", "C3'", "O3'",   "P")},  // here P is in residue i+1
    {NT_zeta,    std::make_tuple("C3'", "O3'",   "P", "O5'")},  // here P and O5' are in residue i+1
    //The following are the orientation dihedral "Chi" for pyrimidine/purine bases
    {NT_pyr,     std::make_tuple("O4'", "C1'",  "N1",  "C2")},  // same as Chi (pyrimidine base)
    {NT_pur,     std::make_tuple("O4'", "C1'",  "N9",  "C4")}   // same as Chi (purine base)
};

The current list of enums and the s_da_map may be extended to include other dihedral angles.

Together, an enum NT_<anglename> and a corresponding s_da_map entry allow the programmer to use the generic iterator Chosen_angle_iterator to calculate the specified dihedral angle. This is because the Chosen_angle_iterator, declared in Linear_polymer_representation, is a boost filter iterator that uses an instance of the class Is_Chosen_angle as a predicate, i.e.:

typedef boost::filter_iterator<Is_Chosen_angle, Dihedral_angle_iterator> Chosen_angle_iterator;

The predicate itself is a T_Linear_polymer_representation::Is_Chosen_angle class instance that returns a boolean indicating whether or not a dihedral angle provided by the Chosen_angle_iterator has the correct "type"– a type here referring to the 4-tuple of atom names, which matches or does not match that of the chosen angle.

template <class ParticleTraits, class MolecularCovalentStructure, class ConformationType, class DAMT>
class T_Linear_polymer_representation<ParticleTraits, MolecularCovalentStructure, ConformationType, DAMT>::Is_Chosen_angle
{
private:
  typedef typename DAMT::key_type    DA_key_type;
  DA_key_type chosen_angle;
 
public:
  Is_Chosen_angle(DA_key_type angle) : chosen_angle(angle) {}
  bool operator()(const Dihedral_angle& t)const{ return t.has_type(chosen_angle);}
};// end class Is_Chosen_angle

As demonstrated in the preceding section, this allows iterating over the desired angles in the chain.

Backbone trace

The SBL also provides a more general mechanism for systematically accessing backbone dihedral angles.

The "backbone trace" is an ordered list (std::vector<std::string> m_backbone_trace;) of atom names referring to the backbone of each residue. It is declared in Linear_polymer_representation.hpp but defined for each polymer (chain) type. For the polynucleotide chain type T_Polynucleotide_chain_representation, the backbone trace is specified as the six atoms P-O5'-C5'-C4'-C3'-O3':

this->m_backbone_trace.push_back("P");
this->m_backbone_trace.push_back("O5'");
this->m_backbone_trace.push_back("C5'");
this->m_backbone_trace.push_back("C4'");
this->m_backbone_trace.push_back("C3'");
this->m_backbone_trace.push_back("O3'");
this->m_backbone_trace_size = this->m_backbone_trace.size();

(This can be compared to the three atoms N-CA-C used to define an amino aid residue in the class SBL::CSB::T_Polypeptide_chain_representation .)

The union of these atoms for all residues constitutes the backbone of the linear chain. The Cartesian coordinates of sequential 4-tuples of the (embedded) atoms indicated in the backbone trace allow computing the backbone torsions 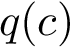$\alpha, \beta, \gamma, \delta, \epsilon, \zeta$ , for each residue among the chain.

This dihedral-angle calculation is handled using a generic algorithm described in section Torsion angles: generic algorithms of the Linear_polymer_representation documentation. Briefly, the offset along the backbone trace defines the position of the first atom of the 4-tuple that is used to calculate the corresponding backbone dihedral angle.

Depending on the offset value, which can be negative, any needed covalently-linked atoms from neighboring residues are automatically supplied in order to calculate backbone dihedral angles spanning two successive residues. For example, the angle 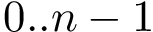$\alpha$ for nucleotide i has an offset of -1, and thus requires, in addition to the coordinates of the atoms P and O5' from that residue, the coordinates of the atoms C3' and O3' from the preceding nucleotide i-1.

This logic is encapsulated in the function get_backbone_torsion_angle(), defined in Linear_polymer_representation:

inline std::pair<bool, FT> get_backbone_torsion_angle(int offset_starting_atom, const Residue& res) const;

To facilitate using this function programmatically, a list of backbone dihedral angle names and a map associating the names with their corresponding offset values is provided:

// Backbone names vector and corresponding offset map specifying backbone dihedrals.
this->da_backbone_names = {"NT_alpha", "NT_beta", "NT_gamma", "NT_delta", "NT_epsilon", "NT_zeta"}; // Defines angle order
this->da_backbone_offset_map =  {
  {"NT_alpha", -1},
  {"NT_beta", 0},
  {"NT_gamma", 1},
  {"NT_delta", 2},
  {"NT_epsilon", 3},
  {"NT_zeta", 4}
};  // Offset in backbone_trace specifying first atom of backbone dihedral 4-tuple

Iterating through the list of names allows calculating the backbone dihedral angles in sequential order along the chain, as shown in the preceding section.

Accessing the ribose dihedral angles

Many linear polymers harbor side chains, with perhaps the most familiar examples being the diverse amino-acid side chains in a polypeptide chain. As opposed to backbone dihedral angles, whose definitions often involve atoms from neighboring residues, side chain angles are defined using atoms contained entirely within the residue itself.

For such a situation the SBL provides a T_Linear_polymer_chain::Ordered_chain_iterator, which iterates over the dihedral angles implicitly defined by a vector of atom names, which starts from a specified backbone atom.

Currently both the Polypeptide_chain_representation and Polynucleotide_chain_representation implement the Ordered_chain_iterator using a Chi_iterator, in which the name "Chi" stems from the polypeptide chain usage. Each chain type also declares and defines a SIDE_CHAIN_ATOMS_REFERENCE_TABLE, which is a map relating each residue name to the relevant vector of atom names.

In Polynucleotide_chain_representation.hpp, this "side chain" vector is composed of the atoms of the ribose sugar, beginning with the C4' atom in the nucleotide backbone and wrapping around the ribose ring, then extending to include two heavy atoms in the pyrimidine or purine base. In Polynucleotide_chain_representation.hpp one thus sees:

template <class ParticleTraits, class MolecularCovalentStructure, class ConformationType>
const std::map<std::string, std::vector<std::string>>
T_Polynucleotide_chain_representation<ParticleTraits, MolecularCovalentStructure, ConformationType>::SIDE_CHAIN_ATOMS_REFERENCE_TABLE = {
  {"A", {"C4'", "O4'", "C1'", "C2'", "C3'", "C4'", "O4'", "C1'", "N9", "C4"}},
  {"G", {"C4'", "O4'", "C1'", "C2'", "C3'", "C4'", "O4'", "C1'", "N9", "C4"}},
  {"C", {"C4'", "O4'", "C1'", "C2'", "C3'", "C4'", "O4'", "C1'", "N1", "C2"}},
  {"T", {"C4'", "O4'", "C1'", "C2'", "C3'", "C4'", "O4'", "C1'", "N1", "C2"}},
  {"U", {"C4'", "O4'", "C1'", "C2'", "C3'", "C4'", "O4'", "C1'", "N1", "C2"}},
};

In the case of the polynucleotide chain, the standard ribose dihedral angle names (see Figure above) are Nu_0, Nu_1, ... whereas the polypeptide usage is Chi_1, Chi_2, ...

The ribose ring torsion angle names along with the nucleotide base Chi dihedral angle name are specified in a simple vector of std::string

// Sidechain dihedral-angle names vector

this->da_sidechain_names = {"Nu_0", "Nu_1", "Nu_2", "Nu_3", "Nu_4", "Nu_0b", "Chi"};

As mentioned above, and as can be seen from the IUPAC figure shown at the top of this section, one should keep in mind that the ribose angle Nu_0b is coaxial with the standard definition Nu_0, and the ribose ring angle Nu_3 is coaxial with (and anti-parallel to) the backbone angle delta.

Example code

The following example is the tutorial example presented in section Using the Nucleic_acid and Polynucleotide representations snippet by snippet :

Applications

This package also offers several useful programs to inspect properties of nucleic acids / their conformations:

sbl-na-info.exe: loads nucleic acid chain(s) form a PDB file, and delivers a variety of statistics (number of nucleotides of each type, center of mass of the structure, calculation of internal coordinates and average statistics, etc.) Note that the corresponding code is intended to provide examples for developers who wish to use this package to develop novel applications.