 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|

Authors: G. Carrière and F. Cazals and C. Robert
The current package is used to represent the two main classes of biomolecules offered in the SBL:
The main goal is to provide a coherent interface in term of iterators, to easily access all relevant pieces of information via iterators:
Biomolecules: a mix of geometry, topology, biophysics, and biology. Biomolecules in general and polypeptide chains (PC in this package) in particular are complex objects. Their description indeed involves
It should be stressed that these three categories of information exist independently and may be used independently. For example:
Indices. As detailed in Section (Advanced/critical) Atoms and indices, the manipulation of atoms involves the following sets of indices:
Finally, recall that an atom is termed embedded if it has Cartesian coordinates. In particular, all missing atoms in a PDB files are stored in the graph representing the molecule, but are not embedded.
class PDBFileParser : defines int mAtomID = 0; (class member) Function PDBFileParser::ParseCoordinate(int modelNr) performs the increment: ++mAtomID;
Concepts. We briefly review the main concepts used in this package, and refer the user to the template parameters of the class SBL::CSB::T_Linear_polymer_representation for precise definition. These concepts are:
Base::s_da_map = {
{P_phi, std::make_tuple("C", "N", "CA", "C")},
{P_psi, std::make_tuple("N", "CA", "C", "N")},
{P_omega,std::make_tuple("CA", "C", "N", "CA")}
};
And for nucleic acids: Base::s_da_map = {
{NT_alpha, std::make_tuple("O3'", "P", "O5'", "C5'")}, // O3' here is in residue i-1
{NT_beta, std::make_tuple("P", "O5'", "C5'", "C4'")},
{NT_gamma, std::make_tuple("O5'", "C5'", "C4'", "C3'")},
{NT_delta, std::make_tuple("C5'", "C4'", "C3'", "O3'")},
{NT_epsilon, std::make_tuple("C4'", "C3'", "O3'", "P")}, // here P is in residue i+1
{NT_zeta, std::make_tuple("C3'", "O3'", "P", "O5'")}, // here P and O5' are in residue i+1
//The following are the orientation dihedral "Chi" for pyrimidine/purine bases
{NT_pyr, std::make_tuple("O4'", "C1'", "N1", "C2")}, // same as Chi (pyrimidine base)
{NT_pur, std::make_tuple("O4'", "C1'", "N9", "C4")} // same as Chi (purine base)
};
Iterators. Iterators used to access a named piece of information are implemented using boost filtered iterators.
Let us take two examples:
typedef boost::filter_iterator<Is_Heavy, Atoms_iterator> Heavy_iterator;
typedef boost::filter_iterator<Is_Chosen_angle, Dihedral_angle_const_iterator> Chosen_angle_const_iterator;
Notations. Since we deal with branched polymers, we assume the following quantities are well defined:
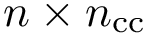
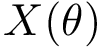
![$[N, CA, C]$](form_704.png)
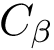

A dihdedral angle is defined by a 4-tuple, corresponding in practice to four atoms of the molecular covalent structure (a boost graph). Given a covalent structure and a specific covalent angle, the goal is therefore to have a generic procedure to identifying these four atoms.
BB torsion angles. For a backbone trace of size 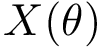
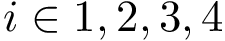
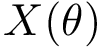
Indexing the atoms of the backbone trace with ![$s\in [0,s-1]$](form_708.png)
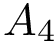
In total, we therefore get 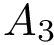
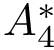
![$o\in [-2,s-1]$](form_712.png)
![$\traceBB[ (s+o) \mod s]$](form_713.png)
Assuming 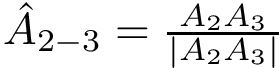
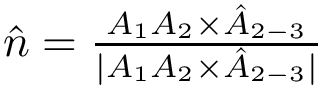



Therefore it suffices to provide 3 functions:
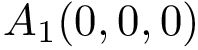
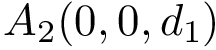
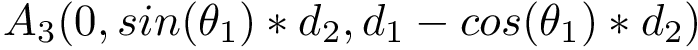
 |
| Backbone torsion angles with a backbone trace of size |
The description above applies to a side chain whose atoms are linearly ordered.
In that case, we assume that the table 
(Important) accessors. The implementation of the generic functions presented in the previous section use the following generic accessors:
The following comments are in order:
inline std::pair<bool, const Atom*> get_atom(const std::string& atom_name, const Residue& res) const; inline std::pair<bool, const Atom*> get_incident_atom(const std::string& incident_atom_name, const Atom& atom) const; inline std::pair<bool, FT> get_backbone_torsion_angle(int offset_starting_atom, const Residue& res) const;
The backbone trace mentioned above enables processing coherently proteins and nucleic acids.
Side chains tough requires a specific processing. However, the following is a generic iterator used to process all sides chains coherently:
//! \brief Generic dihedral angle iterator for arbitrary ordred atom chain
class Ordered_chain_iterator;
The ordered chain iterator is given an atom names list, corresponding to the side chain, to follow from a starting atom. Each consecutive 4-tuple of atoms encountered by the iterator is then returned as a dihedral angle of the side chain.
At each step the next atom is searched using its name among the incident atoms of the current atom. This process stops when the next atom in the list is not embedded or the end of the list is reached, at which point all available dihedral angles of the side chain have been covered and an iterator end is returned.
The reader is referred to the following classes for more details:
The reader is referred to the following resources for the construction of linear polymers:
The 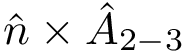
This explains the following design:
Two examples are provided in the SBL: