Nearest_neighbors_graph_builder

Authors: F. Cazals and T. Dreyfus and C. Roth

Introduction

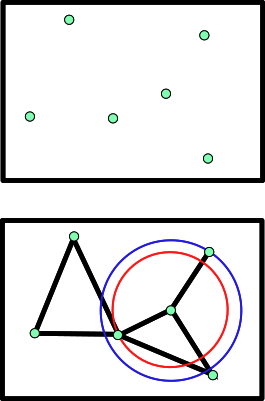
This package provides operations to build a nearest neighbors graph (NN graph for short), basically a Boost Graph from the BGL library, with weights on the edges representing distances.

The NN graph may be defined by linking all vertices to a subset of its neighbors, k closest or in a given range r. All proimity queries rely on an underlying spatial search engine, as explained in the package Spatial_search .

In a BGL graph, vertices and edges do not carry information a priori. To add pieces of information, one uses so-called property maps.

Implementation

Builders

Consider a Boost Graph G from the BGL library such that each vertex is associated to a point. To be precise, it is assumed that the bundle property of the vertex is a point. The package provides a concept of NearestNeighborsGraphBuilder for building such a graph from a range of points [begin,end) and a spatial search engine (search_engine).

In the following, we assume that one is given a search engine either returning the neighbors of a sample within a distance range, or returning the k nearest neighbors of a sample. Three operations are defined:

1) inserting a range of point [begin, end) into a graph G – one vertex is created for each point;

NearestNeighborsGraphBuilder(begin, end, G);

2) connecting a vertex u in G to its neighbors, using a search engine :

NearestNeighborsGraphBuilder(u, search_engine, G);

3) repeating the last operation for every vertices of G :

NearestNeighborsGraphBuilder(search_engine, G);

It is possible to enforce symmetry, i.e. the presence of an edge between two vertices u and v iff both vertices are mutually nearest neighbors. This is achieved by turning the functor's attribute tag compute_sym to true. In that case, the second operation is called once for u and once for v. The third operation needs to be called only once since all vertices are visited.

It should be stressed that the search engine data structure is a model provided by the package Spatial_search. The base parameters for finding the nearest neighbors of a point are provided by the search engine. In particular, selecting the k nearest neighbors (default) or all the neighbors within a range is an option of the search engine. Note that there is no default value for the number of neighbors in the first case.

The package provides two models of builders :

SBL::GT::Nearest_neighbors_graph_builder , a simple builder with no prior knowledge on the NNG.

SBL::GT::Nearest_neighbors_graph_builder_with_edge_weight , a builder assuming that the type of NNG handles weights over the edges, so that distances between vertices bounding an edge can be stored. This is particularly useful when the distance function is heavy to compute, so that it is only computed during the build operation of the NNG.

Module

This package provides the module SBL::Modules::T_Nearest_neighbors_graph_builder_module< ModuleTraits > to build a NNG from an input set of points. The template parameter ModuleTraits must define three types :

Nearest_neighbors_graph : the type representing the NNG, derived from the Boost Graph library;

Nearest_neighbors_distance : the distance functor between two points (it has to define itself the types Point representing a point, and FT representing the coordinates type;

Nearest_neighbors_query< Distance > : a template class for the spatial search engine, parametrized by a distance functor between vertices of the NNG;

When dealing with points in a high dimensional space, storing and duplicating the input points may be expensive. To overcome this limit, we always use the vertex representation of the points in the NNG, so that only vertices may be copied and duplicated. This results on a search engine defined over the vertices of the NNG rather than the points themselves. This also explains why the search engine is templated by a distance functor between vertices. This distance functor between vertices is defined internally to the module based on the input distance functor between points.

The main options of the module T_Nearest_neighbors_graph_builder_module are:
–num-neighbors int: Target number of neighbors for each vertex.
–distance-range int: Distance range specification.
–nng-sym bool: Symmetric NNG ie connects two vertices iff they are mutual nearest neighbors.
–nng-connected int: Attempt connecting the NNG by iteratively increasing the number of neighbors; halt if NNG is connected, or if the prescribed num of neighbors is reached.
–nng-file int: Skip calculations by loading the NNG from a file.

Examples

Simple builder

This example shows how to build the NNG of 2D points built on 100x100 grid, setting four neighbors per point.

#include <SBL/GT/Nearest_neighbors_graph_builder.hpp>
#include <SBL/GT/ANN_metric_space_proximity_tree.hpp>
#include <SBL/GT/ANN_meta.hpp>
#include <iostream>
 
 
class Point_type
{
public:
  double x;
  double y;
  Point_type(void) : x(0), y(0){}
  Point_type(const Point_type& p) : x(p.x), y(p.y){}
  Point_type(double i, double j) : x(i), y(j){}
 
  friend std::ostream& operator<<(std::ostream& out, const Point_type& p)
  {
    out << "[" << p.x << " " << p.y << "]";
    return out;
  }
};
 
typedef boost::adjacency_list<boost::vecS, boost::vecS, boost::undirectedS, Point_type> Graph;
typedef boost::graph_traits<Graph>::vertex_descriptor                              Vertex;
 
class Distance
{
public:
  typedef double     FT;
  typedef Vertex     Point;
  Graph* m_G;
  Distance(void):m_G(NULL){}
  Distance(Graph& G):m_G(&G){}
  FT operator()(Vertex p, Vertex q)const
  {
    return sqrt(((*this->m_G)[p].x - (*this->m_G)[q].x)*((*this->m_G)[p].x - (*this->m_G)[q].x) + ((*this->m_G)[p].y - (*this->m_G)[q].y)*((*this->m_G)[p].y - (*this->m_G)[q].y));
  }
};
 
typedef SBL::GT::T_ANN_metric_space_proximity_tree<Distance>   ANN_proximity_tree;
typedef SBL::GT::T_ANN_meta<ANN_proximity_tree>                ANN;
typedef SBL::GT::Nearest_neighbors_graph_builder               NNG_builder;
 
int main(){
 
  std::vector<Point_type> points;
  for(double i = 0; i < 100; i++)
    for(double j = 0; j < 100; j++)
      points.push_back(Point_type(i, j));
 
  Graph G;
  NNG_builder builder;
  builder.compute_sym = true;
  builder(points.begin(), points.end(), G);
 
  Distance dist(G);
  ANN query(dist);
  query.set_query_type(ANN::ANN_BY_K);
  query.set_number_of_neighbors(4);
 
  query.insert(boost::vertices(G).first, boost::vertices(G).second);
 
  builder(query, G);
 
  std::cout << "G has " << boost::num_vertices(G) << " vertices and " 
            << boost::num_edges(G) << " edges." << std::endl;
  return 0;
}

Builder with edge weights

This example performs the same task as previous but with a NNG able to store the distances between pairs of points linked bya nedge in he NNG.

#include <SBL/GT/Nearest_neighbors_graph_builder.hpp>
#include <SBL/GT/ANN_metric_space_proximity_tree.hpp>
#include <SBL/GT/ANN_meta.hpp>
#include <iostream>
 
 
class Point_type
{
public:
  double x;
  double y;
  Point_type(void) : x(0), y(0){}
  Point_type(const Point_type& p) : x(p.x), y(p.y){}
  Point_type(double i, double j) : x(i), y(j){}
 
  friend std::ostream& operator<<(std::ostream& out, const Point_type& p)
  {
    out << "[" << p.x << " " << p.y << "]";
    return out;
  }
};
 
typedef boost::property<boost::edge_weight_t, double>                                             Edge_property;
typedef boost::adjacency_list<boost::vecS, boost::vecS, boost::undirectedS, Point_type, Edge_property> Graph;
typedef boost::graph_traits<Graph>::vertex_descriptor                                             Vertex;
 
class Distance
{
public:
  typedef double FT;
  typedef Vertex Point;
  Graph* m_G;
  Distance(void):m_G(NULL){}
  Distance(Graph& G):m_G(&G){}
  FT operator()(Vertex p, Vertex q)const
  {
    return sqrt(((*this->m_G)[p].x - (*this->m_G)[q].x)*((*this->m_G)[p].x - (*this->m_G)[q].x) + ((*this->m_G)[p].y - (*this->m_G)[q].y)*((*this->m_G)[p].y - (*this->m_G)[q].y));
  }
};
 
typedef SBL::GT::T_ANN_metric_space_proximity_tree<Distance>      ANN_proximity_tree;
typedef SBL::GT::T_ANN_meta<ANN_proximity_tree>                   ANN;
typedef SBL::GT::Nearest_neighbors_graph_builder_with_edge_weight NNG_builder;
 
int main(){
 
  std::vector<Point_type> points;
  for(double i = 0; i < 100; i++)
    for(double j = 0; j < 100; j++)
      points.push_back(Point_type(i, j));
 
  Graph G;
  NNG_builder builder;
  builder(points.begin(), points.end(), G);
 
  Distance dist(G);
  ANN query(dist);
 
  query.set_query_type(ANN::ANN_BY_K);
  query.set_number_of_neighbors(4);
  query.insert(boost::vertices(G).first, boost::vertices(G).second);
 
  builder(query, G);
 
  std::cout << "G has " << boost::num_vertices(G) << " vertices and " 
            << boost::num_edges(G) << " edges." << std::endl;
  return 0;
}