Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Cluster_analysis

Authors: F. Cazals

Goals: Analyzing clusters

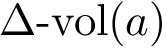
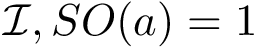
Consider a set of clusters, each given in the form on a $n\times d$ matrix, say $X$. Each cluster may be seen as a point set $P \subset \Rd$.

This package provides a number of geometric analysis on clusters:

  • Distance to the measure
  • PCA scree plots
  • Clustering clusters based on distances between vector subspaces
  • Subpace Embedded Spherical Clusters
  • Separability assessment based on the SVM split ratio
  • Projection median

Distance to the measure

The distance to measure of a point $x$ with respect to a point set $P$ is the average distance to the k-nearest neighbors of $x$ [23] :

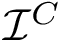
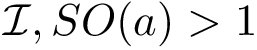
\begin{equation}\dtm{x} = \sqrt{ \frac{1}{k} \sum_{i=1,k} \vvnorm{x-x_{(i)}}^2 }. \end{equation}

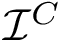
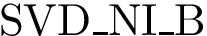
The DTM transform of the point set $P$, denoted $\dtmtrsf{P}$, is the set of all values

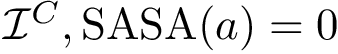
\begin{equation}\{ \dtm{x_i} \}_{i=1,\dots,n} \}. \end{equation}

The DTM is very useful to detect outliers and denoise the dataset. Indeed, in the presence of outliers, a first mode is observed for typical distances between an inlier and its neighbors, while larger (and less pronounced) modes are observed for outliers.


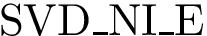
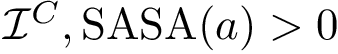
Parameter(s). The number of neighbors. Practically, one uses $k = \sqrt{n}$, or $k = \log n$, see [72] and [22] .

PCA scree plot


PCA scree plots. Upon centering the data matrix 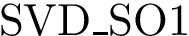$X$, principal components analysis (PCA) provides an indication on directions which carry variance.

The scree plot is the line plot of the eigenvalues of PCA, by decreasing contribution.

The covariance dimension is the minimum number of directions required to explain a predefined fraction of the variance [183] .


Parameter(s). The fraction of explained variance which determines the covariance dimension.

Clustering clusters : the principal angles distance

Once the covariance dimension of each cluster has been determined, a proxy for the cluster is given by its center of mass and the vector space spanned by the principal vectors selected.


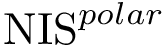
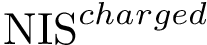
Principal angles: definition. Consider two affine spaces $F\subset \Rd$ and $G\subset \Rd$ such that

\begin{equation}p = \dim F \geq dim G = q \geq 1. \end{equation}

The 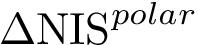$p$ principal angles are recursively defined by

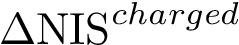
\begin{equation}0 \leq \theta_1 \leq \dots \leq \theta_q \leq \pi/2, \end{equation}

with

\begin{equation}\cos \theta_k = \max_{u\in F} \max_{v\in G} \transpose{u} v = \transpose{u_k} v_k, \end{equation}

under the constraints

\begin{equation}\begin{cases} \vvnorm{u}=\vvnorm{v} =1,\\ \transpose{u} u_i = 0, \forall i:1,dots,k-1\\ \transpose{v} v_j = 0, \forall j:1,\dots,k-1\\ \end{cases} \end{equation}

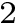
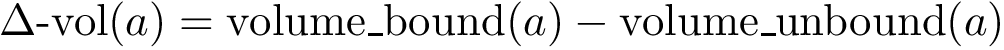
Assume the affine spaces are given by two matrices $Q_F\in \Rd{d\times p}$ and $Q_G\in \Rd{d\times q}$ defining orthonormal basis of $F$ and $G$, respectively. The previous definition translates as

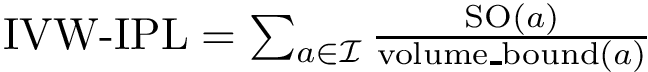
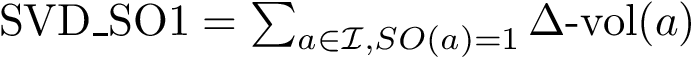
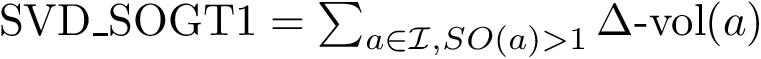
\begin{equation}\max_{\substack{y\in \Rd{p},\\ \vvnorm{y}=1}} \max_{\substack{z\in \Rd{q},\\ \vvnorm{z}=1}} \transpose{Q_Fy} (Q_Gz) = \max_{\substack{y\in \Rd{p},\\ \vvnorm{y}=1}} \max_{\substack{z\in \Rd{q},\\ \vvnorm{z}=1}} \transpose{y}(\transpose{Q_F}Q_G)z. \end{equation}

Consider the SVD of matrix 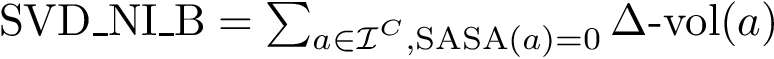$\transpose{Q_F}Q_G = U \Sigma \transpose{V}$. The following holds [100] :

\begin{equation}\begin{cases} [u_1,\dots, u_p ] = Q_F U,\\ [v_1,\dots, v_q ] = Q_G V,\\ \cos \theta_k = \sigma_k, k:1,\dots,q. \end{cases} \end{equation}

If the two affine spaces are given by matrices of rank $p$ and $q$ respectively, one first applies a QR decomposition $M=QR$ to obtain the required orthonormal matrices $Q_F$ and $Q_G$.


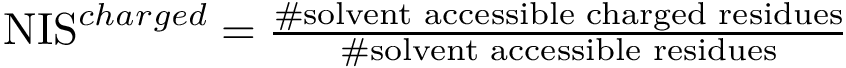
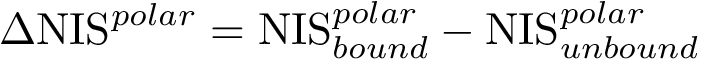
Principal angles: distances. One can therefore compare two clusters using the following distances between subspaces [193] :

  • Distance between the two vector spaces spanned by the principal vectors selected – assumed to be of dimension $k$ and $l$ respectively in the sequel.
  • Distance between the two affine spaces defined by the centers of masses and the principal vectors.

Following ye2016schubert , it is convenient to distinguish:

  • Grassmann distance – a true distance:

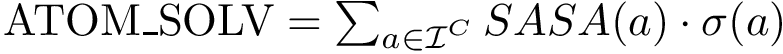
    \begin{equation}\delta(A,B) = \big( \sum_{i=1}^{min(k,l)=l} \theta_i^2 \bigr)^{1/2} \end{equation}

  • Grassman premetric – only satisfies the symmetry:

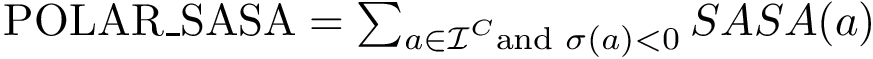
    \begin{equation}d_{\infty}(A,B) = \big( \sum_{i=1}^{max(k,l)=l} \theta_i^2 \bigr)^{1/2} \end{equation}

Clustering clusters : Hausdorff affine distances


The Hausdorff affine distance. For a point $x$ and an affine space $A$, let $\distproj{A}{x}$ be the distance between $x$ and its orthogonal projection onto the affine space $A$. Consider two point sets $P_A$ and $P_B$, and denote $A$ and $B$ the corresponding affine spaces.

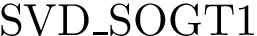
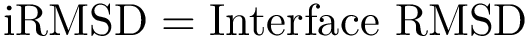
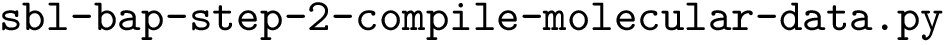
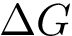
We define the one-sided Hausdorff affine distance between the point set $P_A$ and the affine space $B$ as

\begin{equation}\distHAOS{B}{P_a} = \max_{x\in P_A} \distproj{B}{x}. \end{equation}

Mimicking the Hausdorff distance, we define the Hausdorff affine distance between $P_A$ and $P_B$ as

\begin{equation}\distHA{P_A}{P_B} = \max( \distHAOS{B}{P_A}, \distHAOS{A}{P_B} ). \end{equation}

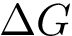
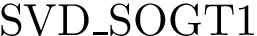
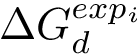
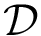
To compute the distance from $x$ to an affine space of dimension $k$ is represented by an orthonormal matrix $M_A$ – of shape $d\times k$ and a reference point $a$:

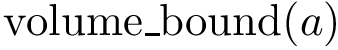
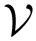
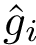
  • Form the vector $v=x-a$, and project it onto the affine space, that is compute $proj(v)=M_A \transpose{M_A} v$. (The latter product compute projects $v$ onto the basis vectors; the former perform a base change to move back to the reference frame.)
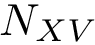
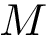
  • Compute the norm of the orthogonal component $\vvnorm{v - proj(v)}$.
To compute a distance using vector spaces rather than affine spaces, use $v=x$ instead of $v=x-a$.



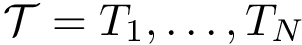
The Average/mean Hausdorff affine distance. In case of outliers, the previous distance put emphasis on the maximum distances.

To tame down this difficulty, define the average one-sided Hausdorff affine distance between the point set $P_A$ and the affine space $B$ as

\begin{equation}\distMHAOS{B}{P_a} = \bigl( \frac{1}{\size{P_a}} \sum_{x\in P_A} \distproj[p]{B}{x} \bigr)^{1/p}. \end{equation}

Mimicking the Hausdorff distance, we define the average/mean Hausdorff affine distance between $P_A$ and $P_B$ as

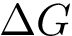
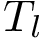
\begin{equation}\distMHA{P_A}{P_B} = \max( \distMHAOS{B}{P_A}, \distMHAOS{A}{P_B} ). \end{equation}

Distance from a point $x$ to an affine space defined by a point $a$ and an orthonormal basis $B$.


Parameter(s). The dimension of the vector spaces compared is determined by the fraction of explained variance used to determine the covariance dimension.

Subspace Embedded Spherical Clusters


SESC. The following is developed in [goldenberg2024subspace] .

Given a point set in 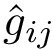$\Rd$, we define a subspace-embedded spherical cluster (SESC) as a spherical cluster of center $c$ embedded into an affine subspace $V$ of $\Rd$. The corresponding distance reads as

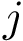
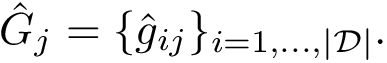
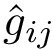
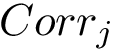
\begin{equation}\dSESC^2 = \vvnorm{\compperp{x-c}}^2 + \mu \max \left(0, \vvnorm{\comppara{x-c}}^2 - \eta \frac{1}{n-1}\sum_{x_i\in D_\ell} \vvnorm{ \comppara{x_i-c}}^2 \right) \end{equation}


Parameter(s). Two hyperparameters:

  • $\mu$: control the balance between the orthogonal and within-subspace distances.
  • $\eta$: controls the radius of the sphere in the affine subspace $V$, and therefore those points outside the sphere representing the cluster – say outliers.
One expects some correlation between between the median DTM and the radius of the SESC sphere.


A SESC defined in the full ambient space of the data is a spherical cluster. Its point can be used as the centerpoint of the dataset, serving as a multidimensional median. In doing so, increasing $\eta$ to include more inliers yields an increase of the SESC radius. Thus, the SESC center can be seen as a parameterized multidimensional median. See [goldenberg2024subspace] for a comparison with the projection median defined below.



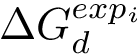
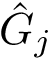
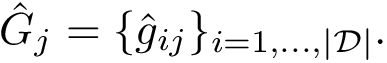
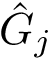
Associated Bayesian Information Criterion – BIC. Consider a cluster of dimension $k$. Defining its orthonormal basis and its center requires respectively $k(d-1)$ angles, and $d$ Cartesian coordinates. The associated BIC value is derived in [goldenberg2024subspace] .

Separability assessment based on the SVM split ratio

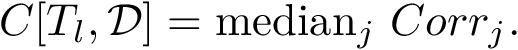
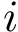
Support vector machines (SVM) is a classical tool to perform classification [171] . Of particular interest is the maximum margin separation , that is the width of the slab separating two point sets. Computing this margin boils down to a quadratic problem. Misclassified items can be tolerated, using a so-called regularization of the optimization problem.

Given a point set, a natural question is to ask whether this point set is naturally separable . We provide this insight in two steps:

  • solve kmeans for $k=2$;
  • compute the maximum margin separation for the labels provided by kmeans.

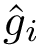
We summarize with the gap/span ratio , namely the ratio between the maximum margin width, and the extent of the projection of all samples onto the line perpendicular to the separating hyperplanes.


Parameter(s). The regularization coefficient 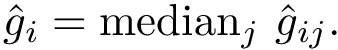$C$ to enlarge the separation margin while tolerating misclassified points.

Projection median

Notions of high dimensional medians generalizing the univariate median are useful concepts to obtain a notion of center point of a point set, see [122], [191] and references therein.

Various such generalizations have been proposed, in including the Fermat-Weber point which minimizes the sum of Euclidean distances to data points, the Tukey median defined as any point whose Tukey depth is at least 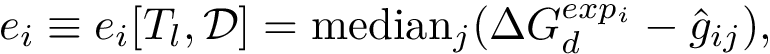$\geq n/(d+1)$, and the projection median.

The projection median is defined by projecting the dataset onto random lines, computing the univariate median for each projection, and computing a weighted average of the data points responsible for these univariate medians, see [81] and [18] . It is an elegant, stable and remarkably effective generalization of the univariate median. This package provides an implementation of the projection median as a weighted sum of the input points [82] .

Using Cluster_analysis

This package provides the script sbl-cluster-analysis.py, whose input(s) and output(s) are as follows.

Input: Specifications and File Types

Input:

  • A directory containing individual cluster files, or one cluster file. The format taken as input is a txt format directly loaded into a 2D numpy array.

Output: Specifications and File Types

Output:

  • A table summarizing the statististics for all analysis
  • A correlation plot for the SESC radius and the DTM
  • A histogram for the DTM transform
  • A scree plot – with a number of directions is the covariance dimension
  • Two dendograms providing a clustering of all clusters (if more than one), using the Grassmann premetric and the Grassmann distance. NB: both computed with a number of directions equal to the covariance dimension.

Selected implementation notes

PCA related analysis

We use the PCA class from SciKitLearn. The following points are worth noticing:


Covariance dimension. Selection of the covariance dimension as a function of the explained variance: 

pca = PCA(n_components = explained_var_target_value, svd_solver='full')

Note that the principal directions are accessed via pca.components_


Projection onto affine space. Projection of a point 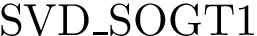$x$ onto the affine space defined by a reference point $a$ and an orthonormal basis $B$:

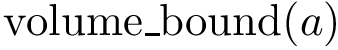
point = X[i,:] # flat array (d,)
if Y_com is None: # vector mode
    vec = point
else:             # affine mode
    vec = point - Y_com

# Project the vector onto the affine space. with d1 the dim of the vector space
# (d,d1)x(d1,d)x(d,1) yields a (d,) flat array: pt in the ambient space
v_proj = Y_obasis @ (Y_obasis.T @ vec.T) # flat array (d,)
v_ortho = vec-v_proj
# Compute the distance
d = np.linalg.norm(v_ortho)

External dependencies

The previous analysis are implemented in the following modules of the package Clustering_analysis: Point_cloud_DTM_filtering, Principal_angles, SVM_cluster_challenger.

The dependencies are as follows:

  • Numerical calculations are carried out with numpy.
  • Distance to the measure: uses the Gudhi library, and in particular the DTMDensity class
  • PCA scree plots: uses the PCA class from SciKitLearn
  • Clustering clusters based on distances between vector subspaces: uses the PCA class from SciKitLearn
  • Subpace Embedded Spherical Clusters: the implementation associated with [goldenberg2024subspace] ; to be released in the SBL.