Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Authors: F. Cazals and T. Dreyfus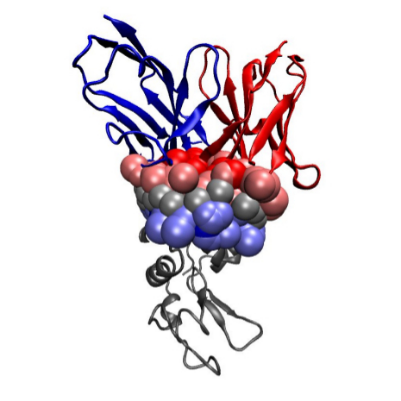

Space_filling_model_interface

Goal: Dissecting Macro-molecular Interfaces

In the sequel, we consider a molecular structure associated with a molecular system Molecular_system and possibly the associated labels MolecularSystemLabelsTraits.

In the simplest case, each system corresponds to one partner in a complex. In a more general setting, as we shall see, a system provides a hierarchical decomposition of a partner. Note that the notion of system is oblivious to the precise geometric representation: in short, a system is defined by a collection of balls, which may be atoms or pseudo-atoms. For the sake of generality, these balls are called particles. At this stage, we just notice that when the particles represent atoms, the geometric model used is the solvent accessible model.

In this context, Space_filling_model_interface is a package of applications computing a parameter free representation of macro-molecular interfaces between systems, based on the 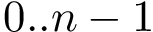$\alpha$-complex of the particles. The benefits of such a model, over classical ones such as the distance footprint (the sets of particles within a prescribed distance threshold), or the particles losing solvent accessibility have been discussed in detail in the literature (see [45] , [51] ) and can be summarized as follows:

  • The interface model is parameter free;
  • It detects pairs of interface particles, either from the partners forming a complex, or from mediators (e.g. water molecules squeezed in-between the partners);
  • It defines a cell complex (a union of surfaces) separating the partners, and amenable to a precise description in terms of patches (connected components), surface area, curvature, particle composition;
  • It qualifies interface particles and Voronoi tiles as a function of their depth at the interface, thus generalizing the classical core-rim models.

These features are bound to two geometric constructions, namely the Voronoi diagram of the particles, and the associated 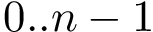$\alpha$-complex. In particular, the rich mathematical structure of these constructions allows deriving all the aforementioned parameters without any third party algorithm or construction. These parameters proved instrumental to unveil novel insights on the location of conserved residues at interfaces, on the polarity of interface residues, or on interfacial water dynamics that were obtained in [30] , [39] , [45] .

Space_filling_model_interface is based on generic c++ code, so that new applications are easily obtained for specific biophysical models, e.g. for specific atomic or coarse-grain models. By default, the following atomic resolution applications of Space_filling_model_interface are provided:

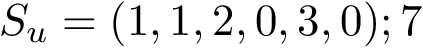
  • $\text{\sblintervorabw}$ , to model atomic resolution binary complexes which may involve interfacial water molecules.
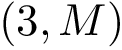
  • $\text{\sblintervorigagw}$ , to model atomic resolution immunoglobulin - antigen complexes (IG-Ag), the IG being decomposed hierarchically into its heavy and light chains.

Applications of Space_filling_model_interface for coarse-grain models with one or two pseudo-atoms per residue is also provided.

Using Intervor: dissecting non hierarchical interfaces

In this section, we model the interaction between two partners $A$ and $B$, mediated by interfacial water molecules $W$.

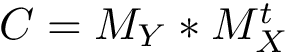
The input is assumed to be a high resolution crystal structure of the complex, so that the particles represent atoms, using their atomic group radii. We represent this atomic structure by its solvent accessible model, that is, the radius of each particle is enlarged by the radius of a water probe, typically 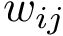$r_w=1.4\AA$.

These constructions are illustrated for the case of an IG (partner $A$) - Ag (partner $B$) complex whose interaction is mediated by water molecules ( $W$).

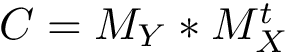
Calculations are performed using the program using the program 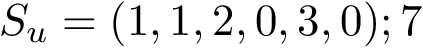$\text{\sblintervorabw}$.

Pre-requisites

Molecular System's Labels

To specify a binary complex, we need to identify the partners and qualify their geometry: these two aspects correspond to the specification of molecular labels MolecularSystemLabelsTraits and of a molecular geometry.

Labeling refers to the assignment of labels to the particles MolecularSystemLabelsTraits . Each molecular system actually has a label falling on one of the three following categories:

  • The partners' labels: they correspond to the particles of the molecules whose interaction is under scrutiny. For a binary complex, there are two labels, which we call $A$ and $B$ by default.
  • The mediators' labels: they correspond to particles sandwiched in-between the partners. The most common mediator is the water molecule, generally called mediator $W$. Since, as noticed above, we work with group radii to account for the absence of hydrogen atoms, a water molecule reduces to its oxygen atom.
  • The extras' labels: they correspond to the remaining particles (e.g. ions, metabolites). If any, all extra particles may be labeled $X$.

Geometric Model

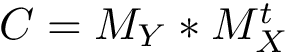
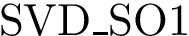
The molecular geometry refers to the geometric representation of the complex studied. In this case, since we take as input a high resolution crystal structure, we use a solvent accessible model. This model is used to build two geometric structures:

  • the regular triangulation of the particles, from which the dual Voronoi diagram can be obtained;
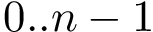
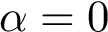
  • the $\alpha$-complex associated to this regular triangulation, for $\alpha = 0$.

For a thorough description of these construtions and of the software used, the reader is referred to the manuals of the CGAL library , and in particular to the Regular_triangulation_3 and Alpha_shape_3 packages.

Voronoi Interfaces

In this section, we sketch the interface model, which is precisely exposed in [51] , and which is illustrated on Fig. Voronoi interfaces.

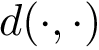
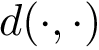
Assume that the particles from the molecular complex studied have been assigned labels. In the sequel, we focus on edges of the $0$-complex such that the two particles found at the endpoints of each such edge have different labels.

An interface mediator particle is a particle whose label is of the mediator type, and which is sandwiched in-between the partners, in the following sense: this particle makes at least one edge with each partner in the $0$-complex.


The typical case is that of water molecules: while water molecules sandwiched in-between the partners at the interface are of interest to study the interaction, those only bound to one partner are not — see Fig. Voronoi interfaces (b). Thus, in the sequel, mediator only refers to oxygen atom of a sandwiched water molecule, as just defined.

An interface edge is an edge of the $0$-complex such that the labels of its two particles are different, and are either both partner labels, or partner label and mediator label.


An interface Voronoi facet is the dual in the Voronoi diagram of an interface edge of two particles.


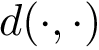
The Voronoi interface associated to two labels is the set of Voronoi facets dual of the interface edges. Our focus is actually on three types of interfaces:

  • the bicolor interface(s), corresponding to Voronoi interfaces between the partners. On our example, there is one such interface, the $AB$ interface.
  • the mediated interfaces, corresponding to Voronoi interfaces between any partner and the mediator. On our example, there are two such interfaces, namely $AW$ and $BW$. Gluing mediated interfaces $AW$ and $BW$ results on the mediated interface $AW-BW$.
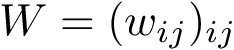
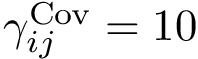
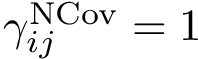
  • the tricolor interfaces, corresponding to the merge of bicolor and mediated interfaces of the partners and mediator. On our example, there is one such interface, namely $ABW=AB\cup (AW-BW)$.
These notions are illustrated on Fig. Voronoi interfaces. Note in particular that on the toy system of Fig. Voronoi interfaces (a), there is only one mediator particle (in grey) at the interface, namely $w_1$. Note also that on the real IG-Ag complex of Fig. Voronoi interfaces (b c d), the interface $AB$ has three connected components, which get sealed by the interfaces involving the water molecules.


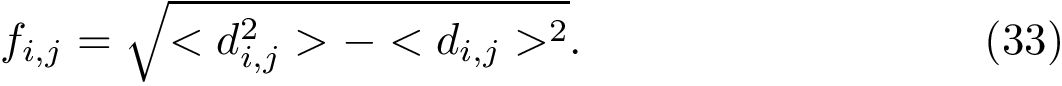
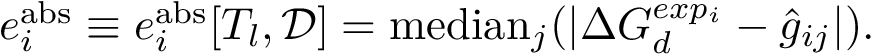
Voronoi Interfaces

(a) 2D illustration (b c d) Illustration for an IG-Ag complex, whose interaction is mediated by water molecules.

(a) The Voronoi diagram of four balls (one red particle, one blue particle, two gray water molecules is shown in solid lines). Each ball has been clipped to its Voronoi region, defining its Voronoi restriction . The $\alpha$-complex, for $\alpha=0$, identifies pairs of restrictions which intersect, here three pairs: $(a_1,b_1)$ defines the $AB$ interface between the two partners, $(a_1,w_1)$ and $(b_1,w_1)$ respectively define the $AW$ and $BW$ interfaces. (b) Side view of the IG-Ag complex, PDB code 1vfb, with the interface particles identified. Note the water molecules (gray) squeezed in-between the two partners. (c) The bicolor interface $AB$ features one Voronoi facet for each pair of particles labelled $A$ and $B$ found in the $0$-complex. Each such Vononoi facet corresponds to a direct interaction between the partners. Note also the interfacial water molecules punching holes at this interface. (d) The tricolor interface, defined as the union of the $AB$ and $AW-BW$ interfaces. The Voronoi facets have been color coded as a function of their distance to the boundary of the Voronoi interface.

For visualizing the Voronoi Interfaces, we recommend you install VMD (see the VMD web site): first load the input PDB file, then load the output visualization state files. The loading of visualization state files may be long, but is a lot faster using the fastload VMD script delivered with the library (in the scripts/vmd directory).


Main specifications

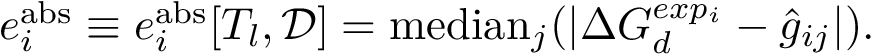
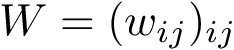
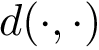
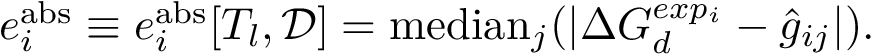
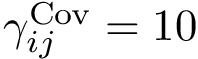
The main specification for 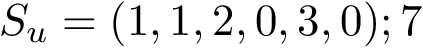$\text{\sblintervorabw}$ are as follows:

Input. An input PDB file and a specification of the partners (PDB chains).

Main options.

The main options of the program $\text{\sblintervorabw}$ are:
-f string: PDB file of the input molecule
-P string: specifiation of the chains of one partner (use it twice for both partners)
–interface-viewer string(=none): create a file for visualizing the interfaces with vmd or pymol


Main output.

  • main log file: suffix .log.txt
  • AB structure classifier: suffix structure_classifier.xml. XML archive listing particles per partner and contacts between partners.
  • AB Voronoi Interfaces xml file: suffix AB_interfaces.xml. XML archive containing the serialized Voronoi interfaces between A and B.
  • AB interfaces VMD file: suffix AB__interfaces.vmd. Visualization state file of the Voronoi interfaces between A and B for the VMD software.

Optional output.

Comments.

Statistics with PALSE

Bicolor and mediated interfaces come with a number of built-in geometric and topological statistics, which are provided per connected components — see [51] for details:

  • Topology: number of patches (i.e connected components or c.c.), holes in the patches;
  • Geometry: number of interface edges, surface area and curvature of the Voronoi facets, buried surface area of the interface atoms, length of the perimeter of the Voronoi interface.
  • Biochemistry: number of particles per patch, tagging of these particles as a function of their types and properties–the PDB atom names and user defined annotations as explained in ParticleAnnotator.

Tricolor interfaces also have specific built-in statistics:

  • Topology: variation of the number of patches upon merging the bicolor and mediated interfaces, as the latter typically bridge gaps between connected components of bicolor interfaces.
  • Shelling order: an interface can be shelled into concentric shells, so as to define a depth of the particles at the interface, thus going beyond the traditional dissection of interface particles into a core and a rim.

Assuming that we run intervor over a number of binary complexes, one would want to know statistics about the number of interface particles, or the interface surface area across the complexes. The following python script uses PALSE over the generated xml files to get these statistics:

Interface string codes

In a manner analogous to multiple sequence alignments, it is often useful to inspect on the sequence which a.a. are at the interface. This functionality is provided by the script sbl-intervor-ABW-atomic-interface-string.py, which can be called right after intervor itself:

sbl-intervor-ABW-atomic.exe -f data/1vfb.pdb -P AB -P C -d results
sbl-intervor-ABW-atomic-interface-string.py -f 1vfb.pdb -p AB -q C -d results

For example, one obtains the following for chain A – note the three stretches corresponding to the 3 CDRs: 

---------------------------N-HNY----------------YY-TT--D----------------------------------FWST-R-----------
The previous script sbl-intervor-ABW-atomic-interface-string.py computes the string code in two steps. First, all particles at the interface are collected. Second, the a.a. contributing these particles are identified. The first step itself deserves a comment. Recall that serialized xml files use ids to avoid the serialization of the same object twice. Consider the following situation: a particle first contributes to the boundary of a connected component (cc) of say the interface AB – it is then serialized when dumping this boundary; then, the same particle is defines a contact in another connected component of the same interface. When this other cc is serialized, the particle in question is referred to with its id, that is, it is not serialized again. For this reason, the collection of interface particles is carried out in three steps:
  1. collect particles defined in the 3 sections of the xml file ie in the particles / contacts / frontier sections of the xml file.
  2. filter particles by chain id – since the focus on a given chain.
  3. keep those particles involved in contacts only. This last step discards particles involved in the definition of the boundaries of cc only.


Using Intervor: dissecting hierarchical interfaces

In the following, we are concerned with the interface of a complex whose partners have a hierarchical structure.

As an application, we consider the particular case of antibodies whose FAB (fragment antigen-binding) can be decomposed into domains contributed by the heave (H) and light (L) chains respectively.

In the SBL, this case is provided by the program 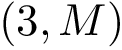$\text{\sblintervorigagw}$.

Motivation

The case of binary interactions mediated by water molecules easily generalizes to the case where each of the partners has a hierarchical structure i.e. can be partitioned into sub-systems.

Consider e.g. an immunoglobulin whose isotype is IgD or IgE or IgG (the IG involves one monomer of two heavy and two light chains, see e.g. the Wikipedia Antibody or the ImMunoGeneTics information system (IMGT) pages), and assume this IG makes up an IG-Ag complex. Such an IG may be considered in three guises:

  • it may be decomposed into its heavy and light chains;
  • or it may be decomposed even further by partitioning each variable domain into three Complementary Determining Regions (CDR) and four framework regions.

Thus, if this IG is involved in an IG-Ag complex, this interaction may be studied at three different levels. As a pre-requisite to do so, we introduce hierarchical decompositions of molecular systems.

Pre-requisites

Molecular System's Labels Forest

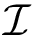
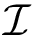
To study interfaces, the complex under scrutiny admits a hierarchical decomposition into labels MolecularSystemLabelsTraits, each of them being identified by a label. That is, we assume that the trees encoding these labels correspond to the partners, the mediators, and the extras. Recall that the molecular system associated with a label $l$ is denoted system( $l$).

Note that each category of labels (the partners, the mediators and the extras) yields a forest of labels whose leaves are called primitive labels. The forest is possibly reduced to a tree, itself possibly reduced to a singleton.

In the following, we call 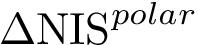$p$ the number of primitive partners and $m$ the number of primitive mediators, and we let $X$ stand for the extra particles. By default, these extra particles are identified but not included in the geometric model of the complex. Note also that in this example, there is a single mediator, namely water.

Primitive and Hierarchical Interfaces

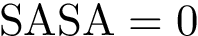
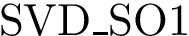
The Voronoi interfaces involving only primitive labels are called primitive interfaces , while all other Voronoi interfaces are called hierarchical interfaces . As illustrated on Fig. Hierarchical interfaces, the two goals are:

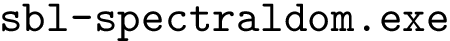
  • To provide information on the $\binom{p}{2}$ primitive bicolor interfaces. Note that for a pair of partners' labels having a common ancestor $l$, the corresponding information corresponds to contacts within the system( $l$).
  • To provide multi-scale information, exploiting the hierarchical structure of each hierarchical label.

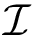
Assuming that the partners' forest and the mediators' forest are given, we first compute all the primitive interfaces in three steps, illustrated on Fig. Hierarchical interfaces for the case of an IG-Ag complex:

  • First, each particle is assigned its primitive label.
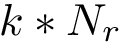
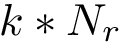
  • Second, a primitive bicolor interface is computed for each couple out of the $\binom{p}{2}$ pairs involving two primitive partners, and a primitive mediated interface is computed for each triple out of the $m\binom{p}{2}$ triples involving two primitive partners and one primitive mediator.
  • Third, $m\binom{p}{2}$ primitive tricolor interfaces are created, by merging the appropriate primitive bicolor and mediated interfaces.
    The three kind of primitive interfaces (bicolor, mediated, tricolor) can also be defined for the hierarchical labels, exploiting the hierarchy induced by the partners' forest and the mediators' forest. We illustrate this process for our IG-Ag complex.
The previous mechanism is illustrated on the IG-Ag complex, which involves three primitive partner labels, namely $H, L, Ag$. These labels result in three primitive bicolor and three primitive mediated interfaces, as represented on the matrices of Fig. Hierarchical interfaces.


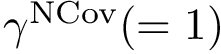
Note that the interfaces provide information on intra-molecular contacts thanks to the interface 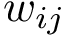$LH$. Note also that the hierarchical interfaces involving $IG$ and $Ag$ are decomposed as follows:
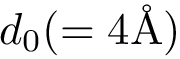
Hierarchical bicolor interface: 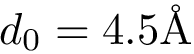$IGAg = (L \cup H)Ag = LAg \cup HAg$
Hierarchical mediated interface: 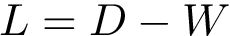$IGW-AgW =(L \cup H)W-AgW = (LW-AgW) \cup (HW-AgW)$
Hierarchical tricolor interface: 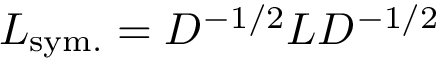$IGAgW = IGAg\cup (IGW-AgW)$

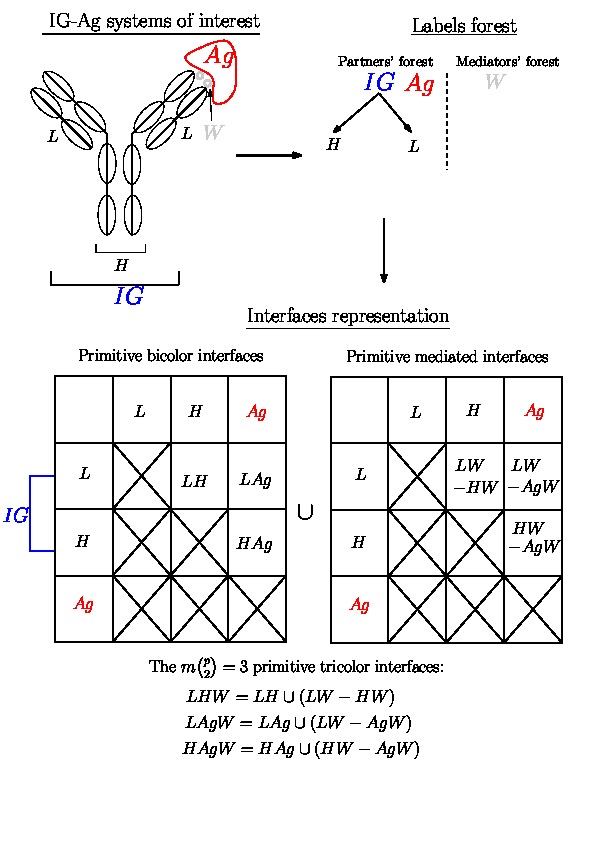Hierarchical interfaces

Decomposition of the IG-Ag complex into molecular systems and hierarchical interfaces (Top Left) Schematic representation of an IG-Ag complex with the different labels of the molecular systems involved. (Top Right) Corresponding partners' and mediators' forests. Note that the partners' forest has two trees. (Bottom) Representation of all possible primitive interfaces (bicolor and mediated on the matrix, tricolor under the matrix).

Main specifications

Input. A PDB file for the IG - Ag complex. We ambition to study the interfaces between the heavy and light chains vs the antigen.

The syntax is almost identical to the one we saw before, except that the heavy and light chains have to be specified separately, e.g. -igL A -igH B -ag C).

Main options.

The main options of the program $\text{\sblintervorigagw}$ are:
-f string: PDB file of the input molecule
–igL string: specifiation of the light chains of the immunoglobulin
–igH string: specifiation of the heavy chains of the immunoglobulin
–ag string: specifiation of the chains of the antigen
–interface-viewer string(=none): create a file for visualizing the interfaces with vmd or pymol


Main output. The main output files are as follows:

  • Main log file, suffix log.txt: log file containing high level information on the run of $\text{\sblintervorigagw}$

The generated log is identical to that generated by 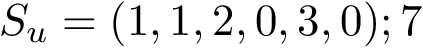$\text{\sblintervorabw}$ , except that there are statistics for each non-empty (bicolor, mediated or tricolor) interface. Furthermore, for each couple of partners with a non-empty bicolor interface, one triple of files (XML, VMD and PDB) is generated.

  • IGAgW structure classifier xml file, suffix structure_classifier.xml: XML archive listing particles per partner and contacts between partners
  • AgIG Voronoi Interfaces xml file, suffix AgIG__interfaces.xml: XML archive containing the serialized Voronoi interfaces between Ag and IG
  • AgIG Voronoi Interfaces VMD file, suffix AgIG__interfaces.vmd: Visualization state file of the Voronoi interfaces between Ag and IG for the VMD software
  • AgH Voronoi Interfaces xml file, suffix: HAg__interfaces.xml: XML archive containing the serialized Voronoi interfaces between the heavy chain of IG and Ag
  • AgH Voronoi Interfaces VMD file, suffix HAg__interfaces.vmd: Visualization state file of the Voronoi interfaces between the heavy chain of IG and Ag for the VMD software
  • AgL Voronoi Interfaces xml file, suffix LAg__interfaces.xml: XML archive containing the serialized Voronoi interfaces between the light chain of IG and Ag
  • AgL Voronoi Interfaces VMD file, suffix LAg__interfaces.vmd: Visualization state file of the Voronoi interfaces between the light chain of IG and Ag for the VMD software
  • LH Voronoi Interfaces xml file, suffix LH__interfaces.xml: XML archive containing the serialized Voronoi interfaces between the light and heavy chains of IG
  • LH Voronoi Interfaces VMD file, suffix LH__interfaces.vmd: Visualization state file of the Voronoi interfaces between the light and heavy chains of IG for the VMD software

Optional output.

Comments.

Visualization, Plugins, GUIs

The SBL provides VMD, PyMOL, and Web plugins for sbl-intervor-ABW-atomic.exe. Launch the VMD plugin from the SBL catalog under the Extensions menu, start the PyMOL plugin by running sbl_intervor_ABW_atomic in the PyMOL command line, and open the Web plugin from the SBL web plugins launcher page (served locally via sbl-web-plugins-launcher). All three plugins expose the same GUI and capabilities.

sbl-intervor-ABW-atomic plugin user interface.

The user interface for the sbl-intervor-ABW-atomic plugin. The typical workflow is: Step 1: Load a molecular structure from a PDB file. Step 2: Specify the two partners by selecting chains from the structure. Step 3: Set other parameters for computation. Step 4: Choose an output directory (optional, a default is provided). Step 5: Launch the computation. Step 6: Inspect the results in the viewer. Step 7: Review the calculation statistics and interface code string in the GUI.

Algorithms and Methods

The algorithm used in the applications of Space_filling_model_interface are standard ones, which we only briefly sketch in the sequel — see [51] for a detailed treatment.

Contacts

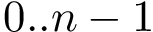
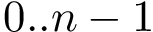
The classification of contacts between particles relies on the $\alpha$-complex of the particles for $\alpha$=0. More precisely, the only information required is the status (singular, regular, interior) of an edge of the regular triangulation of the particles in the $0$-complex. See the Alpha_shape_3 package from CGAL for further details.

Interfaces

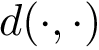
From a topological standpoint, the bicolor and mediated interfaces are so-called manifold interfaces [132] . In a nutshell, this means that a triangle from the regular triangulation contributes at most two edges to this interface. By the Voronoi - Delaunay duality, this also means that the topological neighborhood of a point located in the relative interior of a Voronoi edge bounding an interface Voronoi facet is either a topological disk or half a topological disk. Note that a tricolor interface may not be a manifold interface.

From an algorithmic standpoint, the computation of primitive interfaces relies on two algorithms:

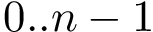
  • The basic construction is that of a manifold interface. To enumerate the connected components of a manifold interface, we perform a breadth first exploration of the Voronoi facets of that interface. Using the duality between a Voronoi diagram and the associated Delaunay (regular) triangulation, this only requires collecting the interface Delaunay edges contributed by a triangle from the $\alpha$-complex.

In particular, bicolor and mediated interfaces are manifold interfaces. See [132] for the details.

  • To build tricolor interfaces from bicolor ones, bicolor interfaces are build first, and are then merged using the Union-Find algorithm.
  • The treatment of hierarchical interfaces is also straightforward. For example, a hierarchical bicolor interface remains manifold: the primitive manifold interface of $AB$ obtained by considering $A$ as a primitive partner is exactly the same than the hierarchical manifold interface of $AB$. This is also true for the hierarchical mediated interface.

Curvatures

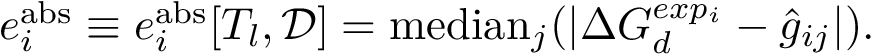
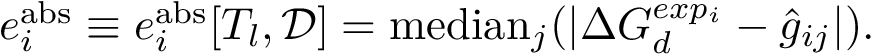
The curvature of each connected component of all Voronoi interfaces (hierarchical or primitive, bicolor, mediated or tricolor) is computed twice, one calculation for each partner. First, all the Voronoi edges in the interior of the connected component involving the selected partner are gathered. We orientate the Delaunay edges dual of the Voronoi faces incident to the Voronoi edges such that the particles in the selected partner are the sources of these Delaunay edges. Then, we compute the curvature associated to a Voronoi edge using:

  • the orientated angle between the two Delaunay edges,
  • the length of the Voronoi edge (finite since it is in the interior of the interface).

The sum of the curvatures of all the interior Voronoi edges of a connected component defines its curvature, and the sum of the curvature of all connected components of an interface defines the curvature of the interface. Note that an unsigned version of the curvature is also computed (when summing the curvatures of interior Voronoi edges, the absolute value of the curvature is considered).

Buried Surface Area

It is also possible, using the option –bsa, to compute the BSA of each partner at the interface, a task taken care of by the package Buried_surface_area . For versions of intervor using atoms, an XML file is dumped, containing the ids of the atoms (atom id, resid, chain id), as well as the BSA. For versions of intervor using pseudo-atoms, only the BSA is dumped.

The type of information recorded on a per particle basis is defined by the template parameter ParticleBSARecord of the class T_Space_filling_model_interface_traits. See also the documentation Buried_surface_area .


Programmer's Workflow

The programs of Space_filling_model_interface described above are based upon generic C++ classes, so that additional versions can easily be developed for protein or nucleic acids, both at atomic or coarse-grain resolution.

In order to derive such versions, there are two important ingredients, that are the workflow class, and its traits class.

The Traits Class

T_Space_filling_model_interface_traits:

The Workflow Class

T_Space_filling_model_interface_workflow:

Jupyter demo

See the following jupyter notebook:

  • Jupyter notebook file
  • Space_filling_model_interface
    In [ ]:

    Space_filling_model_interface

    We dissect non-hierarchical and hierarchical Voronoi interfaces in macro-molecular complexes.

    In the sequel, we consider the following complexes:

    • 1VFB: an antibody (chains A and B) - protein antigen (chain C) complex
    • 2AJF: a protein (spike of SARS-COV-2) and its receptor (RBD)

    For both, we first compute the non-hierarchical Voronoi interface, which just requires specifying which chains make up the two partner. For 1vfb, we further exploit the decomposition of the IG into its H and L chains, which yields a hierarchical Voronoi interface.

    Computing the non-hierarchical Voronoi interfaces

    In [13]:
    import re  #regular expressions
import sys #misc system
import os
import shutil # python 3 only
import matplotlib.pyplot as plt

odir = "results"
if not os.path.exists(odir): os.system( ("mkdir %s" % odir) )
       
   
ifiles = ["data/1vfb.pdb",  "data/2ajf.pdb"]
partners = [("AB", "C"),   ("A", "E")]
def compute_AB_interface(ifile, partners, radius = 0., bsa = False):
    if not os.path.exists(odir): os.system( ("mkdir %s" % odir) )

    exe = shutil.which("sbl-intervor-ABW-atomic.exe")
    if not exe:
        print("Executable sbl-intervor-ABW-atomic.exe not found, exiting")
        return
    
    cmd = "%s -f %s -P %s -P %s --directory %s --verbose --output-prefix \
          --log --interface-viewer vmd --radius-water %f" \
          % (exe,ifile, partners[0], partners[1],odir, radius)
    if bsa:
        cmd += " --bsa"
    print(("Running %s" % cmd))
    os.system(cmd)

    # list output files
    cmd = "ls %s" % odir
    ofnames = os.popen(cmd).readlines()
    print("\nAll output files:",ofnames)

   
print("Marker : Calculation Started")
compute_AB_interface(ifiles[0], partners[0], 1.4, bsa = True)
compute_AB_interface(ifiles[1], partners[1], 1.4)
 

print("Marker : Calculation Ended")

    Marker : Calculation Started
Running /user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-intervor-ABW-atomic.exe -f data/1vfb.pdb -P AB -P C --directory results --verbose --output-prefix           --log --interface-viewer vmd --radius-water 1.400000 --bsa

All output files: ['sbl-intervor-ABW-atomic__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__AB__interfaces.vmd\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__buried_surface_area.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__log.txt\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__structure_classifier.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__AB__interfaces.vmd\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__log.txt\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__structure_classifier.xml\n', 'sbl-intervor-ABW-atomic__structure_classifier.xml\n']
Running /user/fcazals/home/projects/proj-soft/sbl-install/bin/sbl-intervor-ABW-atomic.exe -f data/2ajf.pdb -P A -P E --directory results --verbose --output-prefix           --log --interface-viewer vmd --radius-water 1.400000

All output files: ['sbl-intervor-ABW-atomic__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__AB__interfaces.vmd\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__buried_surface_area.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__log.txt\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_1vfb__P_AB__P_C___alpha_0__structure_classifier.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__AB__interfaces.vmd\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__AB__interfaces.xml\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__log.txt\n', 'sbl-intervor-ABW-atomic__radius_water_1dot4__f_2ajf__P_A__P_E___alpha_0__structure_classifier.xml\n', 'sbl-intervor-ABW-atomic__structure_classifier.xml\n']
Marker : Calculation Ended

    Visualization with VMD

    This package offers two sources of visualization:

    • Interface atoms centric: the vmd file delivered by sbl-intervor-ABW-atomic.exe
    • Interface residues centric: the vmd selection file delivered by sbl-intervor-ABW-atomic-interface-string.py We illustrate these on two complexes below. Note that for each row, the first three images display the output of the Voronoi interface calculation. For the last images, we created a VMD selection displaying all atoms of all interface amino acids.
    In [21]:
    import matplotlib.pyplot as plt
from PIL import Image


fig, ax = plt.subplots(2, 4, figsize=(15,15))

map(lambda axi: axi.set_xticks([]), ax.ravel())

images_1vfb = ["fig/1vfb-complex.png", "fig/1vfb-interface-atoms.png", "fig/1vfb-voronoi-interface.png", "fig/1vfb-interface-residues-all-atoms.png"]
images_2ajf = ["fig/2ajf-complex.png", "fig/2ajf-interface-atoms.png", "fig/2ajf-voronoi-interface.png",     "fig/2ajf-interface-residues-all-atoms.png"]

print("Top row: antibody-antigen complex")
print("Top row: portion of spike of SARS-COV-2 in complex with its RBD")
 
for i in range(0,4):       
    ax[0, i].set_xticks([]); ax[0, i].set_yticks([])
    ax[0, i].imshow( Image.open(images_1vfb[i]) )
    
    ax[1, i].set_xticks([]); ax[1, i].set_yticks([])
    ax[1, i].imshow( Image.open(images_2ajf[i]) )
    
#fig.show()

    Top row: antibody-antigen complex
Top row: portion of spike of SARS-COV-2 in complex with its RBD

    Statistics with PALSE

    Bicolor and mediated interfaces come with a number of built-in geometric and topological statistics, which are provided per connected components -- aka binding patches: topology, geometry, biochemistry.

    Tricolor interfaces also have specific built-in statistics, in particular topology and shelling order.

    Such statistics are easily recovered from the files generated, using PALSE, as we illustrate on a couple of examples. In all generality: just spot the label of interest in the XML file, and get the information with PALSE.

    In [17]:
    from SBL import PALSE
from PALSE import *

def analyze_with_palse():
    database = PALSE_xml_DB()
    odir = "results"
    #database.load_from_directory(odir)
    database.load_from_directory(odir,".*interfaces.xml")

    # interface AB
    num_atoms_at_AB = database.get_leftmost_data_values_from_database("AB_interface_output/AB_interface_statistics/number_of_particles", int)
    surface_areas_at_AB_with_A = database.get_leftmost_data_values_from_database("AB_interface_output/total_Voronoi_area_with_A", float)
    surface_areas_at_AB_with_B = database.get_leftmost_data_values_from_database("AB_interface_output/total_Voronoi_area_with_B", float)
  
    print("Num. atoms at the interface AB:",num_atoms_at_AB)
    print("Surface area, interface AB:", surface_areas_at_AB_with_A)
    #PALSE_statistic_handle.hist2d(surface_areas_at_AB, "hist-interface-areas-AB.eps")

   
    # interface ABW
    num_atoms_at_ABW = database.get_leftmost_data_values_from_database("ABW_interface_output/ABW_interface_statistics/number_of_particles", int)
    print("Num. atoms at the interface ABW:",num_atoms_at_ABW)
    surface_areas_at_ABW_with_A = database.get_leftmost_data_values_from_database("ABW_interface_output/total_Voronoi_area_with_A", float)
    surface_areas_at_ABW_with_B = database.get_leftmost_data_values_from_database("ABW_interface_output/total_Voronoi_area_with_B", float)
    print("Surface area, interface ABW:", surface_areas_at_ABW_with_A)
    
print("Marker : Calculation Started")
analyze_with_palse()
print("Marker : Calculation Ended")

    Marker : Calculation Started
XML: 3 / 3 files were loaded

Num. atoms at the interface AB: [574, 154, 199]
Surface area, interface AB: [1213.0411651475317, 261.2199942850441, 764.9419501876393]
Num. atoms at the interface ABW: [793, 329, 246]
Surface area, interface ABW: [1872.825129408191, 724.0049088370517, 840.3806673038042]
Marker : Calculation Ended

    Visualizing the interface strings

    In [22]:
    import os
import subprocess

cmd = "mkdir resi"
os.system(cmd)

cmd = "sbl-intervor-ABW-atomic.exe -f data/2ajf.pdb -P A -P E -d resi"
os.system(cmd)

cmd = ["sbl-intervor-ABW-atomic-interface-string.py", "-f", "data/2ajf.pdb", "-p", "A", "-q", "E", "-d", "resi"]
s=subprocess.check_output(cmd, encoding='UTF-8')
print(s)

    Ranges of aa for chains of partners: {'A': (19, 615), 'E': (323, 502)}
XML: 1 / 1 files were loaded

XML: 1 / 1 files were loaded


+++Dumping interface string for chain  A
--Min-max resids for string  A (19, 615)
--Chain  A  has  32  interface a.a.: [19, 23, 24, 26, 27, 28, 30, 31, 34, 37, 38, 41, 42, 45, 79, 82, 83, 324, 325, 326, 327, 329, 330, 353, 354, 355, 356, 357, 387, 388, 389, 393]
--Interface code:
S---EQ-KTF-DK--H--ED--YQ--L---------------------------------L--MY------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------TQGF-EN----------------------KGDFR-----------------------------AQP---R------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------


+++Dumping interface string for chain  E
--Min-max resids for string  E (323, 502)
--Chain  E  has  28  interface a.a.: [390, 393, 404, 405, 408, 426, 432, 436, 440, 442, 443, 460, 462, 463, 470, 472, 473, 475, 479, 481, 482, 484, 486, 487, 488, 489, 491, 492]
--Interface code:
-------------------------------------------------------------------K--D----------VI--Y-----------------R-----S---Y---Y-YL----------------F-PD------P-LN-Y---N-YG-Y-TTGI-YQ----------
    In [ ]:

    Computing the hierarchical Voronoi interface

    In [3]:
    def compute_AB_hierchical_interface():

  
    exe = shutil.which("sbl-intervor-IGAgW-atomic.exe")
    if not exe:
        print("Executable sbl-intervor-IGAgW-atomic.exe not found, exiting")
        return
    
    
    ifile = "data/1vfb.pdb"
    odir = "results-hierarchical"
    
    if not os.path.exists(odir): os.system( ("mkdir %s" % odir) )

    cmd = "%s -f %s --igL A --igH B --ag C  --directory %s --verbose --output-prefix --log --interface-viewer vmd" % (exe,ifile,odir)
    os.system(cmd)
    # list output files
    
    cmd = "ls %s" % odir
    ofnames = os.popen(cmd).readlines()
    print("\nAll output files:",ofnames)
    
print("Marker : Calculation Started")
compute_AB_hierchical_interface()
print("Marker : Calculation Ended")

    Marker : Calculation Started

All output files: ['sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__AgIG__interfaces.vmd\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__AgIG__interfaces.xml\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__HAg__interfaces.vmd\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__HAg__interfaces.xml\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__LAg__interfaces.vmd\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__LAg__interfaces.xml\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__LH__interfaces.vmd\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__LH__interfaces.xml\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__log.txt\n', 'sbl-intervor-IGAgW-atomic__radius_water_1dot4__f_1vfb__igL_A__igH_B__ag_C__alpha_0__structure_classifier.xml\n']
Marker : Calculation Ended

    Under VMD, we can now visualize in turn (i) the whole IG-Ag interface, (ii) the interafce between the heavy chain and the antigen, (iii) the interface between the light chain and the antigen, and (iv) the interface between the H and L chains.

    In [ ]:
    In [ ]:
    In [ ]: