 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: A. Roth and F. Cazals and T. Dreyfus
This package provides wrappers for libraries minimizing real valued functions at a given point. The two main libraries that are wrapped are :
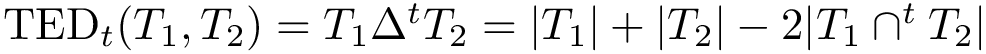
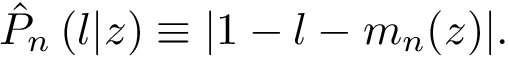
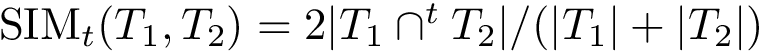
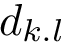
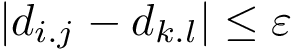
When 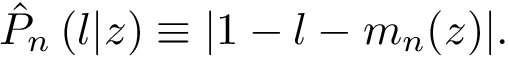
Mathematically, we note that a local minimum is a particular case of a so-called critical point, that is a point where the gradient of the function vanishes. Furthermore, following the Morse lemma, the so-called index of the critical point i.e. the number of negative eigenvalues of the Hessian qualifies its status, from local minimum, to local maximum. Thus, in all generality, methods tracking critical points need to access exact values both for the gradient and the Hessian.
Following classical terminology, a method approximating the Hessian from exact gradients is termed quasi-Newton. For example, the Broyden–Fletcher–Goldfarb–Shanno method is a quasi-Newton method.
In the sequel, when describing methods, by exact partial derivatives, we refer to partial derivatives computed using symbolic differentiation or via automatic differentiation.
Optimization and biophysics differ on one fundamental point.
In optimization, one is often satisfied with a (good enough) local minimum (or maximum).
In biophysics, the enumeration of local minima with sufficiently low potential energy is a critical endeavor, as from statistical physics, macroscopic properties emerge from ensemble properties of conformations located in the catchment basins of such local minima. This enumeration task is precisely that tackled by functions from the package Landscape_explorer, where the domain is a conformational space and the function is the potential energy of a target molecule.
We now explain the main algorithms used to minimize a function.
A large number of methods exist for looking for global or local extrema. Some of them are dedicated to specific functionals (e.g. linear functionals), while some are more general. In this package, our focus is on the latter, and more specifically on iterative methods exploiting 1st and 2nd derivatives .
Two methods are wrapped:
IPOPT : implements a primal-dual interior point method.
L-BFGS : a quasi-Newton optimization algorithm well suited to handle cases with a large number of variables. Indeed, as opposed to BFGS, which stores a fully dimensional inverse Hessian matrix, L-BFGS uses an estimate of this matrix based on a sparse set of vectors.
This package provides a C++ concept RealValueFunctionMinimizer defining a functor parametrized by the function to optimize : it takes an initial point as input, and returns a pair (bool, point) such that that boolean value is true iff a local minimum has been found, and the point is the local minimum if the local minimum has been found. The requirements of the concept RealValueFunctionMinimizer are :
std::pair<bool, Point*> operator()(const Point* p)const;
The package provides two models of this concept :
In both cases, the template parameters are :
IFT operator()(const InternalPoint* p)const;
void operator()(const InternalPoint* p, InternalPoint* q)const;
Note that both for the function and the gradient functors, the types for numbers and points refer to the internal types to the libraries(Ipopt or LBFGS++), not the types used outside of these libraries. This is important in particular when a particular data structure is required in a program that is not the one used in one of these libraries : in such a case, one has to count the cost of converting its own data structures toward and backward these internal data structures.
Both models share identical tuning parameters :
The following example instantiates the Ipopt algorithm without any constraint for the norm function, and minimizes an input D-dimensional point. It repeats the operation one thousand times for computing an average time of computation.
The following example instantiates the LBFGS algorithm, and minimizes an input D-dimensional point. It repeats the operation one thousand times for computing an average time of computation.
This package offers base applications for quenching molecular conformations, i.e finding local minima in the vicinity of the given conformations :