 |
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
|
Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
|
Authors: F. Cazals and T. Dreyfus and C. Roth
This package provides methods to build transition graphs, i.e. graphs connecting local minima of an energy landscape, across index one saddles.
This package provides various methods dealing with the construction of transition graphs (TG), i.e. graphs connecting local minima and index one saddles (Fig. fig-tg-builder-himmelblau-basins-TG and definition def-transition-graph). The TGs built are meant to be used as input for the analysis presented in the following packages:
In the sequel, we consider a conformational ensemble 
. We may also assume that the local minimum 
associated with each conformation 
, that is obtained by following the negative gradient of the potential energy, is known. Following classical terminology, this minimization process is called quenching. This set is denoted 
. We assume that the (potential) energy 
of each conformation is known.
Methods to build TG are provided in three settings:
From a database of stationary points (local minima and index one saddles).
From a conformational ensemble 
with 
a set of conformations, and 
the local minima associated to all conformations – obtained upon quenching.
From a dense sampling .
 |
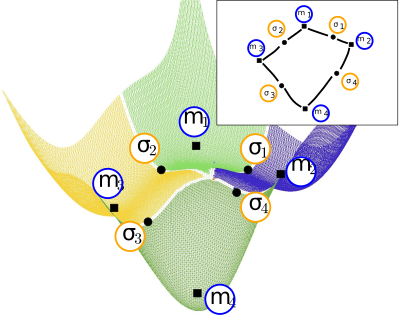
| Himmelblau: (Compressed) Transition graph (A) The landscape of Himmelblau, decomposed into the catchment basins of the four local minima (B) The transition graph, with one node for each critical (i.e., stationary) point (C) The compressed transition graph, where the information associated with saddles is stored in the edges joining local minima. |
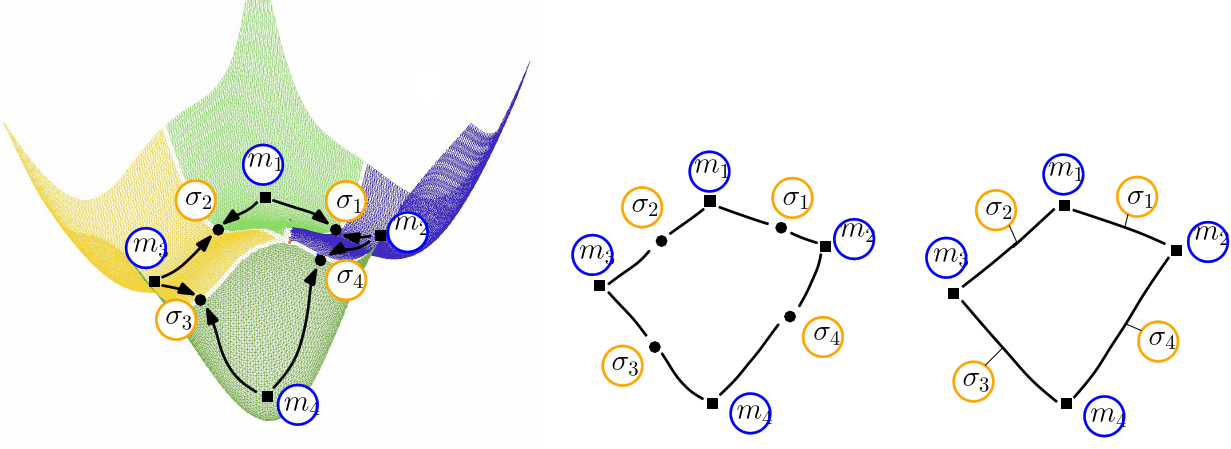
We first recall the following two definitions (details def-transition-graph)):
The construction of the transition graph also output a weight for each local minimum. The weight is expected to code the probability of occupancy of the basin associated with the local minimum. Note that when persistence is used, the weight is the sum of the weights from the basins associated to the persistent local minimum.
Because weights are only on minima, we use the compressed transition graph representation, and set the weights on the vertices. There are two ways to set the weights:
TG built from a DB of stationary points. The weight of a local minimum is the normalized Boltzmann's factor computed using the energy of this local minimum. Beware of units for systems with reduced units, such as BLN69 for which both Boltzmann constant and temperature are set to unity. The following Python script computes the normalized Boltzmann's factor:
import sys, numpy
with open(sys.argv[1]) as fp:
exps = [numpy.exp(-float(l)) for l in fp]
vals = [v/numpy.sum(exps) for v in exps]
for v in vals: print(v)
TG built from sample points. The weight of a local minimum is the fraction of samples in the basin of the local minimum.
In that case, the user must specify energies only – since weights are computed from the fraction of samples in a basin.
When a database of connected critical points (local minima and index one saddles) is available, building a transition graph is trivial.
We note that compressed transition graphs (rather than transition graphs) are built (definition def-compressed-tg), to minimize the memory footprint.
Main options.
Input. The input consists of five files:
Main output.
Optional output.
Comments.
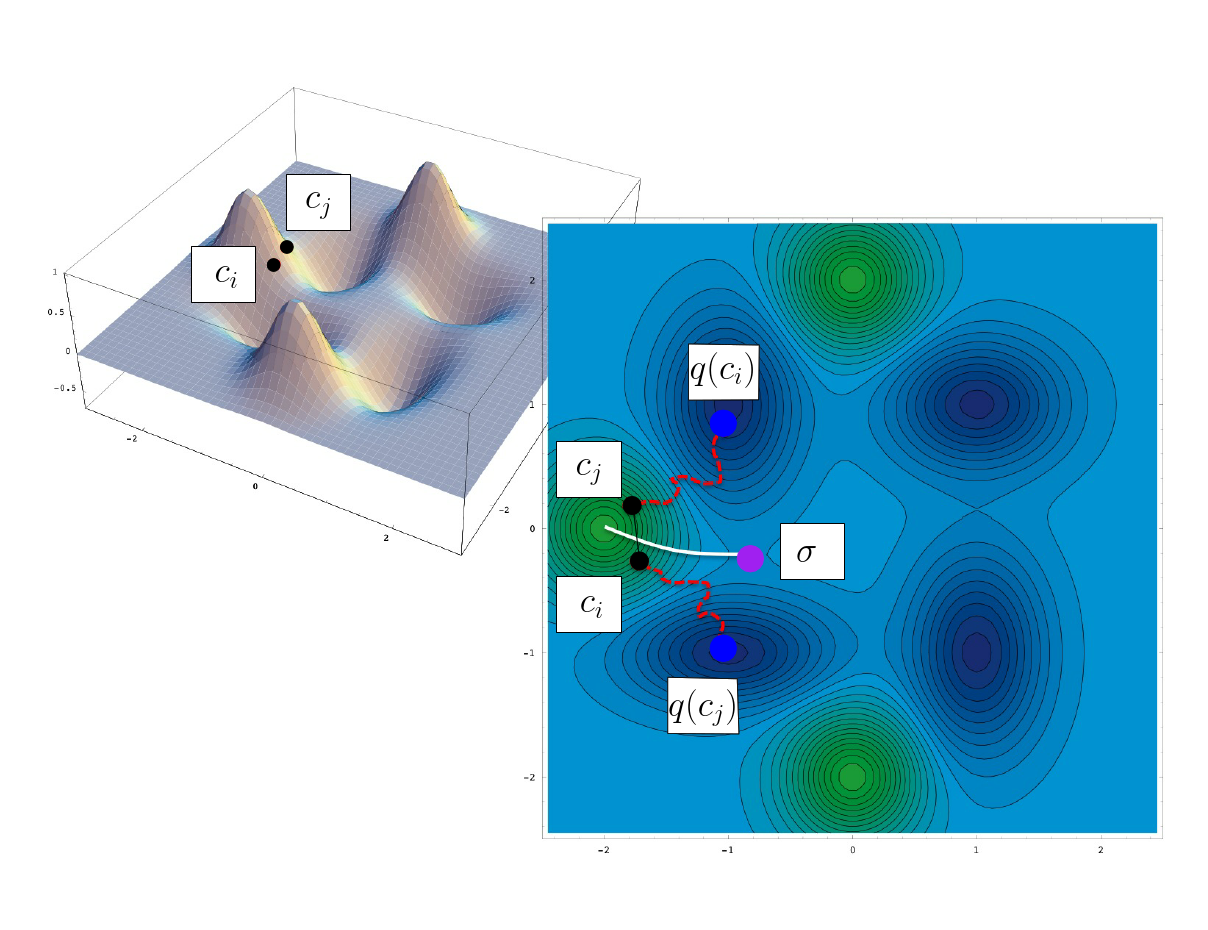
Consider now the case where a plain sampling has been obtained, together with the local minimum associated with each sample (obtained by quenching) [165], [133] . Let us also assume that the transitions themselves have not been computed. In this case, one can locate pairs of conformations, say 
satisfying two conditions (see Fig. fig-morse-stable-unstable-manifolds-algo-flow-backward):
the conformations and 
are neighbor – their distance (for some suitable distance metric) is less than a user defined threshold;
and quench to different local minima. Such a pairs is said to witness a bifurcation.
Note that the same two local minima may be witnessed by multiple pairs. For small enough value of the distance threshold, the sample with lowest energy amidst such pairs witnesses the adjacency of the catchment basins of and 
. An algorithm to detect such pairs is sketched below, see section Algorithms and Methods.
Main options.
Input.
Main output.
Optional output.
Comments.
Consider finally the cases where only samples are known – that is the local minimum associated with a conformation is unknown. Also assume that the neighborhood of has been densely sampled, and that has been connected to a set of nearest neighbors, using a nearest neighbor graph (NNG, definition def-nng). We estimate the gradient of the potential energy at using its neighbors in the NNG. More precisely, we estimate the gradient using the neighbor 
of yielding the maximum slope. Starting from and iteratively following this estimated gradient eventually leads to a sample having all its neighbors above it. One can use this sample as a substitute 
for .
Main options.
Input.
Main output.
Optional output.
Comments.
In the following, we sketch the construction of the TG from a collection of points and associated local minima. The reader is also referred to the package Morse_theory_based_analyzer for further details (see also the MTBA module in the workflow, Fig. fig-tgb-workflow).
Assume that one is given a conformational ensemble together with the corresponding quenched points . The algorithm consists of two main steps (Fig. fig-morse-stable-unstable-manifolds-algo-flow-backward):
Step 1: Nearest neighbor graph. We build a NNG on the conformations – see package Nearest_neighbors_graph_builder, and in addition endow each sample with an edge to . Note that this connection directly links each sample to its local minimum.
, such that (i) belongs to the lower star of (recall that samples are processed by increasing height), and (ii) 
. We also say that these samples witness a bifurcation. When such a pair of samples is found, we record the path from to through the samples and . The collection of all such paths defines a transition graph between the vertices from the set . 
, or (iii) they are located in the neighborhood of a degenerate critical point (a so-called monkey saddle). Our method, which uses solely the samples, does not distinguish between these situations. 
– the dimension of the whole configuration space minus one, which leaves ample space. and .
 |
| Identifying the connexion between the basins of two local minima by quenching two samples and Sample is quenched to while is quenched to . The samples and sit across the (white) ridge separating the basins of their respective |
The programs of Transition_graph_of_energy_landscape_builders described above are based upon generic C++ classes, so that additional versions can easily be developed.
In order to derive other versions, there are two important ingredients, that are the workflow class, and its traits class.
T_Transition_graph_builder_from_sampled_energy_landscape_traits:
T_Transition_graph_builder_from_sampled_energy_landscape_workflow:
For an analysis on the star of a vertex in a weighted graph, we recommand the use of the program sbl-energy-landscape-analysis-graph-star.exe, defined in the package Energy_landscape_analysis .
See the following jupyter notebook:
Useful functions
from SBL import SBL_pytools
from SBL_pytools import SBL_pytools as sblpyt
help(sblpyt)
When a database of connected critical points (local minima and index one saddles) is available, building a transition graph is trivial.
We note that compressed transition graphs (rather than transition graphs) are built, to minimize the memory footprint.
The options of the runFromDatabase method in the next cell are:
weights: optional plain text file listing minima weights for a weighted transition graph
Nb: by default, no persistence is used. But the executable used can also use persistence.
from SBL import TG_builders
from TG_builders import *
sbl_exe_name = "sbl-tg-builder-lrmsd.exe"
odir= "tmp-results-db-lrmsd"
tg1 = TG_builders.build_transition_graph_fromDB(sbl_exe_name,
"data/bln69_database_minima_conformations.txt", "data/bln69_database_minima_energies.txt",
"data/bln69_database_transitions_conformations.txt", "data/bln69_database_transitions_energies.txt",
"data/bln69_database_transitions.txt",
odir,
"data/bln69_database_minima_weights.txt")
print(tg1)
sblpyt.list_directory_content(odir)
Consider now the case where a plain sampling has been obtained, together with the local minimum associated with each sample (obtained by quenching). Let us also assume that the transitions themselves have not been computed. In this case, one can locate pairs of conformations, say $(c_i, c_j)$ satisfying two conditions:
the conformations $c_i$ and $c_j$ are neighbor – their distance (for some suitable distance metric) is less than a user defined threshold;
the conformations $c_i$ and $c_j$ quench to different local minima.
Such a pairs is said to witness a bifurcation. Note that the same two local minima may be witnessed by multiple pairs. For small enough value of the distance threshold, the sample with lowest energy amidst such pairs witnesses the adjacency of the catchment basins of $q(c_i)$ and $q(c_j)$.
The options of the runFromMinima method in the next cell are:
Nb: by default, no persistence is used. But the executable used can also use persistence.
from SBL import TG_builders
from TG_builders import *
sbl_exe_name = "sbl-tg-builder-lrmsd.exe"
odir= "tmp-results-quench-lrmsd"
tg = TG_builders.build_transition_graph_from_minima(sbl_exe_name,
"data/bln69_sampling_samples_conformations.txt", "data/bln69_sampling_samples_energies.txt",
"data/bln69_sampling_quenched_conformations.txt", "data/bln69_sampling_quenched_energies.txt",
"data/bln69_sampling_samples_to_quench.txt", odir)
print(tg)
sblpyt.list_directory_content(odir)
odir = "tmp-results-quench-lrmsd"
images = []
images.append( sblpyt.find_and_convert("disconnectivity_forest.eps", odir, 100) )
images.append( sblpyt.find_and_convert("persistence_diagram.pdf", odir,100) )
sblpyt.show_row_n_images(images, 100)
Consider finally the cases where only samples are known – that is the local minimum $q(c_i)$ associated with a conformation $c_i$ is unknown. Also assume that the neighborhood of $c_i$ has been densely sampled, and that $c_i$ has been connected to a set of nearest neighbors, using a nearest neighbor graph (NNG). We estimate the gradient of the potential energy at $c_i$ using its neighbors in the NNG. More precisely, we estimate the gradient using the neighbor $c_k$ of $c_i$ yielding the maximum slope. Starting from $c_i$ and iteratively following this estimated gradient eventually leads to a sample having all its neighbors above it. One can use this sample as a substitute $\tilde{q}(c_i)$ for $q(c_i)$.
The options of the runFromSamples method in the next cell are:
persistence: ersistence threshold for removing not-persistent basins due to noisy data
Nb: by default, no persistence is used. But the executable used can also use persistence.
from SBL import TG_builders
from TG_builders import *
sbl_exe_name = "sbl-tg-builder-euclid.exe"
odir = "tmp-results-sampling"
tg = TG_builders.build_transition_graph_from_sampling(sbl_exe_name, "data/himmelblau_rand_points.txt", "data/himmelblau_rand_heights.txt", odir)
print(tg)
sblpyt.list_directory_content(odir)
odir = "tmp-results-sampling"
images = []
images.append( sblpyt.find_and_convert("disconnectivity_forest.eps", odir, 100) )
images.append( sblpyt.find_and_convert("persistence_diagram.pdf", odir,100) )
sblpyt.show_row_n_images(images, 100)
1.9.1