Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Table of Contents

Authors: F. Cazals and T. Dreyfus and N. Malod-Dognin

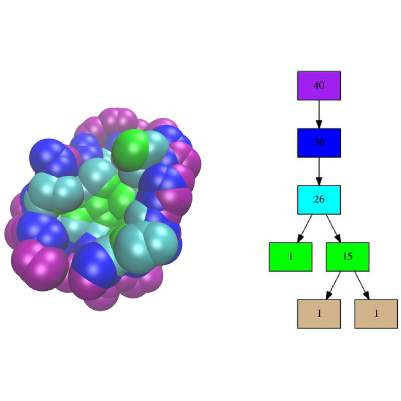
Space_filling_model_shelling_diagram_comparison

Goals: Comparing Binding Patches

A binding patch (patch for short) of a molecular model is a set of atoms involved in an interaction with a partner in a complex, as defined in the applications of Space_filling_model_shelling_diagram_surface_encoding.

The classical way to compare two patches $P_1$ and $P_2$ consists of finding subsets of atoms $M_1\subseteq P_1$ and $M_2\subseteq P_2$, in one-to-one correspondence – in particular $M_1$ and $M_2$ are of the same size, in such a way that there exists a rigid motion superimposing $M_1$ onto $M_2$. The quality of such a match is typically assessed using the least RMSD.

This approach has two main limitations:

  • It relies on the computation of a maximum clique, an NP-hard problem [106] .
  • Finding set of atoms in correspondence via a rigid motion is rather strict, and does not allow comparing set of atoms undergoing flexible deformations.

Space_filling_model_shelling_diagram_comparison gets around these two difficulties by proposing structural comparisons favoring either geometric or topological features, as illustrated on Fig. fig-lego-interface-flat-curved-montage.

To present them, recall that Space_filling_model_shelling_diagram_surface_encoding computes a topological encoding of binding patches, by aggregating the atoms of a binding patch into shells, a shell being a collection of neighboring atoms located at a fixed distance of the binding patch boundary. The relative position of these shells yields an encoding of the patch as an ordered tree known as the atom shelling tree, see Fig. fig-shelling-tree.

The fact that the tree is ordered is important: using dynamic programming, ordered trees can be compared via a simple operation known as the Tree Edit Distance (TED) [23] . In a nutshell, the algorithm for TED is a generic algorithm computing the cost of morphing a tree $T_1$ into a tree $T_2$, based upon three costs, namely the deletion of a node from $T_1$, the insertion of a node into $T_1$, and the transformation of a node of $T_1$ into a node of $T_2$.

Interestingly, adjusting the semantics of the three aforementioned operations allows defining two types of TED calculations:

  • $\tedt$: a TED favoring the topological comparison of the patches. Intuitively, this comparison favors isotopologic sets of atoms: the matching between the sets of atoms $M_1$ and $M_2$ is defined at the shell — rather than binding patch level, and the matching matches shells of the same size regardless of the 3D positions of the atoms.
  • $\tedg$: a TED favoring the geometric comparison of the patches. Intuitively, this comparison favors quasi-isometric sets of atoms: the matching between the sets of atoms $M_1$ and $M_2$ is defined at the shell — rather than binding patch level, and the matching seeks within shells subsets of atoms which can be super-imposed using a rigid transformation.

Notations For both the intersection $\cap^x$, the symmetric difference $\Delta^x$ and the similarity score $\text{SIM}_x$, $x$ stands for the used methodology ( $t$: topological TED; $c$: Clique; $g$: geometrical TED). Abusing terminology, we shall indistinctly speak of a shell or its node representation in the shelling tree.

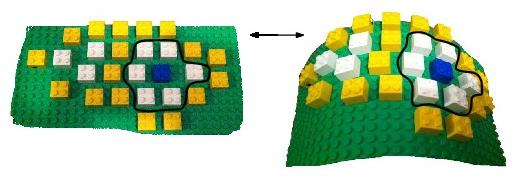An idealized illustration of the topological rigidity handled in Space_filling_model_shelling_diagram_comparison

For the sake of illustration, a fictitious binding patch is presented, each lego block meant to represent one atom. The color coding of the atoms codes the shelling order of the patch, as defined in Space_filling_model_shelling_diagram_surface_encoding. From left to right, the binding patch bends: while the relative position of the atoms in 3D changes, each particular atom retains exactly the same neighbors, which we illustrate with the blue atom. Such a binding patch is termed geometrically flexible, but topologically rigid. Space_filling_model_shelling_diagram_comparison provides methods to assess the rigidity / flexibility of binding patches, either from a geometric or topological standpoint.

Using Compatch: Comparing Two Atom Shelling Forests

This section presents the program $\text{\sblcompatchE}$.

Prerequisites

Topological Comparison with the Tree Edit Distance

Isotopology. A shell $v_1$ of a shelling tree is an ancestor of a shell $v_2$ if there is an oriented path from $v_1$ to $v_2$ in the shelling tree. Two shells $(v_1,w_1)\in T_1$ are isotopologic to the shells $(v_2,w_2) \in T_2$ if either:

  • (i) $v_1=w_1$ and $v_2=w_2$, or

  • (ii) $v_1$ is an ancestor of $w_1$ and $v_2$ is an ancestor of $w_2$, or,

  • (iii) $v_1$ is to the left of $w_1$ iff $v_2$ is to the left of $w_2$ (Recall that trees are ordered).

Two atoms of $T_1$ and two atoms of $T_2$ are isotopologic iff the shells containing them are isotopologic. Between $T_1$ and $T_2$, a subset of atoms $V_1\subseteq T_1$ is isotopologic to a subset $V_2\subseteq T_2$ if there exists a one-to-one mapping between the atoms of $V_1$ and the ones of $V_2$ such that any two atoms in $V_1$ are isotopologic to their counterparts in $V_2$.

Problem statement. The comparison problem reduces to an ordered Tree Edit Distance problem (TED) having the following edition costs.

Adding or deleting a shell $s$ has a cost of $|s|$, since all the atoms of $s$ are added/removed. Morphing a shell $s_1$ into a shell $s_2$ has cost equal to the size of their symmetric difference:

$ |s_1\Delta^{t} s_2| = |s_1|+|s_2| -2|s_1 \cap^{t} s_2| $

.

Note that in this case, since there is no distinction between the atoms, the cost is the absolute value of the difference between the number of atoms in both shells : $|s_1\Delta^{t} s_2| = \mid |s_1|-|s_2| \mid$. However, the general formula is true for all the comparisons that are introduced in this section.


Denoting $|T_1 \cap^{t} T_2|$ the number of isotopologic atoms between $T_1$ and $T_2$, $\tedt{T_1}{T_2}$ is the size of the symmetric difference

$ \tedt{T_1}{T_2} = T_1 \Delta^{t} T_2 = |T_1|+|T_2| -2|T_1 \cap^{t} T_2| $

.

The similarity between two trees is then the number of their isotopologic atoms normalized by the size of the two trees to be in [0,1]:

$ \simt{T_1}{T_2} = 2 |T_1 \cap^{t} T_2| / (|T_1| + |T_2|) $

Geometric Comparisons

Quasi-isometry. Given two shelling trees $T_1$ and $T_2$, two atoms $i$ and $j$ from $T_1$ are quasi-isometric to the atoms $k$ and $l$ from $T_2$ if the euclidean distances $d_{i.j}$ (between $i$ and $j$) and $d_{k.l}$ (between $k$ and $l$) are such that $|d_{i.j} - d_{k.l}|\leq \varepsilon$, with $\varepsilon$ a distance threshold circa 2 $\AA$.

Between $T_1$ and $T_2$, a subset of atoms $V_1\subseteq T_1$ is quasi-isometric to a subset $V_2\subseteq T_2$ if there exists a one-to-one matching between the atoms of $V_1$ and the ones of $V_2$ such that any two atoms in $V_1$ are quasi-isometric to their counterparts in $V_2$. Such matchings have the property that the corresponding Root Mean Squared Deviation of internal distances ( $RMSD_d$) is smaller than $\varepsilon$.

Problem statement.

To favor geometric comparisons, we are interested in finding the largest subset of atoms between $T_1$ and $T_2$ satisfying the aforementioned quasi-isometry condition.

Mimicking Eq. eq-sim-tedt, the similarity between $T_1$ and $T_2$ is:

$ \simg{T_1}{T_2} = 2 |T_1 \cap^{c} T_2| / (|T_1| + |T_2|) $

It can be shown that the previous calculation reduces to a maximum clique calculation [38] .

Mixed Comparison

To strike a balance between geometric and topological criteria, we are interested in finding the subsets of atoms that are isotopologic and where the quasi-isometric constraints are satisfied between the matched shells. Meeting these criteria is amenable to a TED calculation, using the following costs.

The costs for inserting/deleting a shell $s$ is $|s|$. The cost for morphing a shell $s_1$ into a shell $s_2$ is equal to the size of their symmetric difference $s_1\Delta^{c} s_2 = |s_1| + |s_2| - 2|s_1 \cap^{c} s_2|$, where $s_1 \cap^{c} s_2$ is the subset of isotopologic and quasi-isometric atoms, as found by applying the Clique method between the two shells $s_1$ and $s_2$.

Problem statement.

To balance topological and geometric comparisons, we are interested in finding the largest subset of atoms between $T_1$ and $T_2$ that is both quasi-isometric and isotopologic.

Let $|T_1 \cap^{g} T_2|$ be the number of atoms between $T_1$ and $T_2$ that are both isopologic and quasi-isometric.

In this case, $\tedg{T_1}{T_2}$ is the size of the symmetric difference that is:

$ \tedg{T_1}{T_2} = |T_1 \Delta^{g} T_2| = |T_1|+|T_2| -2|T_1 \cap^{g} T_2| $

.

The similarity between two trees is then the size of $|T_1 \cap^{g} T_2|$ normalized by the size of the two trees:

$ \simc{T_1}{T_2} = 2 |T_1 \cap^{g} T_2| / (|T_1| + |T_2|) $

Comparison Between the Topological and Mixed Approaches

Given the computational complexity of purely geometric comparisons, we focus in the sequel on the topological and mixed comparisons.

Both methods respect the isotopologic constraints, but only Clique respects all the isometric constraints. $\tedga$ verifies the isometric constraints $|d_{i.j} - d_{k.l}|\leq \varepsilon$ only when $i$ and $j$ (and thus $k$ and $l$) come from the same shell. Finally, in $\tedta$, the isometric constraints are not verified at all.

This implies that the size of the atomic subsets returned by Clique are smaller than the size of the subsets returned by $\tedga$ which are smaller than the values found by $\tedta$.

Thus, the following holds:

$ \displaystyle \simg{T_1}{T_2} \leq \simc{T_1}{T_2} \leq \simt{T_1}{T_2} $

Also, because of the possibly broken isometric constraints, $\tedga$ may return matchings having $RMSD_d$ values larger than $\varepsilon$.

This section describes the application's options and file formats.

Input: Specifications and File Types

Given the atom shelling trees of two binding patches (XML file format), $\text{\sblcompatchE}$ use the tree-edit-distance based methods to measure their dissimilarity, and also record the optimum tree-edit-script (the sequence of tree-edit operations). An example run of $\text{\sblcompatchE}$ is given as follows:

> sbl-compatch.exe --shelling-forest data/1vfb_atom_shelling_tree_A.xml --shelling-forest data/1vfb_atom_shelling_tree_B.xml --comparison-mode g --directory results --verbose --output-prefix --log
The main options of the program $\text{\sblcompatchE}$ are:
–shelling-forest string: XML archive file of an atom shelling forest (one archive for each shelling forest)
–comparison-mode string(=t): Comparison of shells, either geometric (g) or topological (t)


File Name

Description

Source Atom Shelling Forest xml file Atom shelling tree of the binding patch of the partner A of the IGAg complex 1vfb
Target Atom Shelling Forest xml file

Atom shelling tree of the binding patch of the partner B of the IGAg complex 1vfb

Input files for the run described in section Input: Specifications and File Types .

Output: Comparison and Edit Script

There are two output files that are created from the last command line:

  • one xml file encoding the tree edit script for moving from the source tree to the target tree.
  • one input file for Graphviz (see section Graphviz (Graph visualization)) so as to visualize the matching between the two input atom shelling trees. For the cases where Graphviz is not installed, the option –eps-format tells the program to also dump encapsulated postscript (eps) files.

During its execution, a record on the main steps undertaken is dumped into the called window. This information can be sent stored a log file with the option -l .

PreviewFile Name

Description

General: log file

Log file

Log file containing high level information on the run of $\text{\sblcompatchE}$

Module shelling forests comparison

Comparison xml file

XML file describing how to move from the source tree to the target tree

Click it Comparison dot file

dot file for visualizing the matching between the two input trees using GraphViz

Output files for the run described in section Input: Specifications and File Types, classified by modules – see Fig. fig-compatch-workflow .

For visualizing the shelling forests comparison, we recommend you to install Graphviz (see the Graphviz web site), and using the dot software for drawing the graph from a .dot file. Note that there are other software from the Graphviz library for drawing the graphs with different embedding.

Algorithms and Methods

Topological Comparison with the Tree Edit Distance

The computation of isotopologic atom sets reduces to the classical TED, see [23] , with the insertion / deletion / morphing costs discussed above.

Geometric Comparisons via Maximum Clique Calculation

The computation of quasi-isometric subsets of atoms is rephrased as a maximum clique problem as follows. Let $G_{T_1,T_2}=(V,E)$ be a graph whose vertex set $V$ is depicted by a grid in which each row represents an atom of $T_1$ and each column represents an atom of $T_2$. Matching the atoms $i\in T_1$ and $k\in T_2$ is represented by the vertex $i.k \in V$ (on row $i$, column $k$). $\forall i.k\in V$ and $\forall j.l\in V$ such that $i\neq j$ and $k\neq l$, if $i$ and $j$ are quasi-isometric and isotopologic to $k$ and $l$ then the edge $(i.k, j.l)$ is in $E$. The largest subset of atoms between $T_1$ and $T_2$ that is both quasi-isometric and isotopologic, denoted by $T_1 \cap^{c} T_2$, corresponds to a maximum clique in $G_{T_1,T_2}$.

The maximum clique problem is NP-Hard [106] , and is solved by using Ostergard's algorithm [140] . Note that the isotopology constraints reduce the number of edges in $G_{T_1,T_2}$, thus easing the maximum clique solving process.

Programmer's Workflow

The applications of Space_filling_model_shelling_diagram_comparison described above are based upon generic C++ classes, so that additional versions can easily be developed.

In order to derive such versions, there are two important ingredients, that are the workflow class, and its traits class.

The Traits Class

T_Space_filling_model_shelling_diagram_comparison_traits:

The Workflow Class

T_Space_filling_model_shelling_diagram_comparison_workflow: