Structural Bioinformatics Library
Template C++ / Python API for developping structural bioinformatics applications.
User Manual

Table of Contents

Point_cloud_rigid_registration_3

Authors: F. Cazals and T. Dreyfus

Introduction

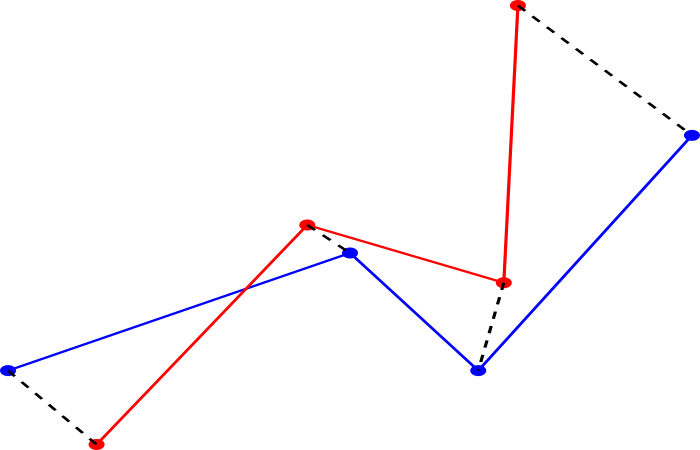
Consider two point sets $X$ and $Y$ of the same size; we also assume an alignment between them, meaning that the i-th point of $X$ is paired with the i-th point from $Y$.

The point set registration consists on finding a spatial transformation aligning $Y$ onto $X$. The registration is said rigid if the distance between all pairs of points is conserved by the transformation. This package defines a rigid registration between two set of 3D points where the spatial transformation is a composition of translations and rotations.

Implementation

Theory

Assume that we want to perform the registration of the point cloud $Y$ onto the point cloud $X$. In doing so, we shall assume that the center of mass (aka centroid) of $X$ is the reference center of mass, and upon applying the optimal rigid motion to $Y$, the centroid of this modified point set will coincide with that of $X$.

The rigid registration is done using a linear algebra algorithm that computes the optimal rotation matrix between the two input set of points using the Singular Value Decomposition (SVD) of their covariance matrix. Basically, once centered on the origin, the covariance matrix $C$ of the two input sets of points $X$ and $Y$ is computed. The SVD of $C = V * S W^t$ then produces orthogonal matrices representing rotations ( $V, W$).

More precisely, the algorithm is as follows :

  • 1) compute the centroids $c_X$ and $c_Y$ of $X$ and $Y$ respectively, so as to center the input set of points, and fills the matrices $M_X$ and $M_Y$ of size $(3,N)$ and $(3,M)$ with the new centered points;
  • 2) compute the covariance matrix $C = M_Y * M_X^t$;
  • 3) compute the SVD of $C = V * S * W^t$;
  • 4) compute the matrix $E$ that is the identity matrix $(3, 3)$, except that $E(2, 2) = \mid C\mid$, and then computes the optimal rotation matrix $U = W * E * V^t$;
  • 5) rotate the matrix $M_Y$ using $U$; denoting $o$ the origin of the coordinate system, further translate the resulting point cloud with the vector $oc_X$ for its center of mass to coincide with that of $X$.

Design

The algorithm is coded in the class SBL::GT::T_Point_cloud_rigid_registration_3< FT >, where FT is the number type used for representing the coordinates of the points (by default, the double type).

The class can be used in two modes :

  • 1) using two point clouds and computing directly the associated rigid registration;
  • 2) using two point clouds to initialize a transformation that can be reused anytime.

Note that the second one is suited to cases where the same transformation has to be applied to a family of point clouds.

The constructor of SBL::GT::T_Point_cloud_rigid_registration_3 takes two containers of points and computes the associated rigid transformation. Then the class provides functors and methods for the aforementioned two modes :

  • 1) Functor taking two point clouds as argument: computes and stores internally the transformation defined by these two point clouds.
  • 2) Method transform taking one point cloud as argument: uses the internal transformation to transform this point cloud.

For both modes, the input points clouds can be represented in three different ways :

  • random-access containers of points (e.g arrays or vectors),
  • pairs of (begin, end) iterators over the containers of points,
  • triples (size, begin, end), corresponding to the size and iterators over containers of the coordinates of the input points.

The last one is useful when the input sets of points are represented by D-dimensional points, for exemple when computing the distance between molecular conformations (see package Molecular_distances)

Examples

Registration with rotated and translated set of points

The following example shows how to perform a rigid registration:

  • A point set is loaded (variable points),
  • This point set is rotated (variable points_transformed),
  • points_transformed in then registered onto points (variable points_registered).
  • It is then checked that points and points_registered coincide (see also the l-RMSD calculation in package Molecular_distances).

Multiple rigid registrations

The following example shows how to store the transformation defined by the rigid registration of a point cloud onto another one, so as to later use this transformation to transform any point cloud.

Note that in this example, variable points2 is registered onto points1, so that the reference centroid is that of point1. Which means that in applying the optimal rigid motion to points3, the centroid of the transformed points3 coincides with that of points1.

Applications

This package offers alors a program for performing the rigid registration between a reference set of 3D points and a collection of sets of 3D points : sbl-align-point-clouds-3.exe . An input set of 3D points is represented as a D dimensional point, where D is divisable by 3. A file listing D dimensional points is a text file where each point is represented by its dimension followed by its coordinates. Note that breaklines are not considered, so that having one D dimensional point per line, or one 3D point per line are both acceptable :

6 0 0 0 1 1 1

or

6
0 0 0
1 1 1

The program sbl-align-point-clouds-3.exe takes two files as input : the first one containing one D dimensional point representing the reference set of points, and the second containing any number of D dimensional points.